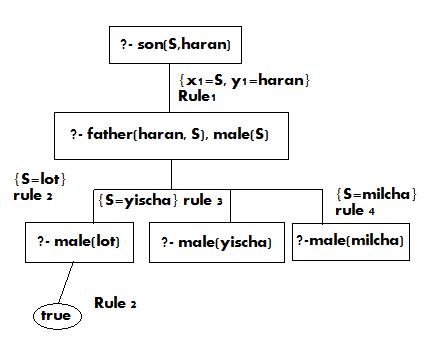
תכנות לוגי
| |||||||
Read other articles:

Untuk ekonom Kanada, lihat John James Deutsch. John M. Deutch Direktur Intelijensi Pusat ke-17Masa jabatan10 Mei 1995 – 15 Desember 1996PresidenBill ClintonWakilWilliam O. StudemanGeorge Tenet PendahuluJames WoolseyPenggantiGeorge TenetWakil Menteri Pertahanan Amerika SerikatMasa jabatan11 Maret 1994 – 10 Mei 1995[1]PresidenBill Clinton PendahuluWilliam PerryPenggantiJohn P. WhiteMenteri Tingkat Rendah Pertahanan untuk Akuisisi dan TeknologiMasa jabatan2 April 19...

Public university in Tacoma, Washington, United States University of Washington TacomaMottoLux sitMotto in EnglishLet there be light[1]TypePublic universityEstablished1990; 34 years ago (1990)Parent institutionUniversity of WashingtonChancellorSheila Edwards LangeAcademic staff347Administrative staff340Students5,135[2]Undergraduates4,291Postgraduates696LocationTacoma, Washington, United States47°14′41″N 122°26′16″W / 47.2448°N ...

artikel ini tidak memiliki pranala ke artikel lain. Tidak ada alasan yang diberikan. Bantu kami untuk mengembangkannya dengan memberikan pranala ke artikel lain secukupnya. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Ulan-Ude Aviation Plant (UUAZ, Russian: Улан-Удэнский авиационный завод) adalah perusahaan saham gabungan Rusia yang mengkhususkan diri dalam pembuatan pesawat. Ulan-Ude Aviation Plant ini terletak di Ulan-Ude, Buryatia. Perusah...

Artikel ini mungkin terdampak dengan peristiwa terkini: Invasi Rusia ke Ukraina 2022. Informasi di halaman ini bisa berubah setiap saat. Republik Rakyat LuhanskЛуганская Народная Республика (bahasa Rusia)— Republik — Bendera Lambang Lagu resmi: Государственный гимн Луганской Народной РеспубликиGosudarstvennyy gimn Luhanskoy Narodnoy Respubliki(Indonesia: Himne Nasional Republik Rakyat Luhan...

2018 studio album by Black Veil BridesValeStudio album by Black Veil BridesReleasedJanuary 12, 2018Recorded2016–2017StudioFoxy Studios, Los Angeles, CaliforniaGenre Hard rock heavy metal glam metal Length46:37Label Lava Republic Producer John Feldmann Jake Pitts Black Veil Brides chronology Black Veil Brides(2014) Vale(2018) Re-Stitch These Wounds(2020) Singles from Vale The OutsiderReleased: December 21, 2016[1] My VowReleased: September 28, 2017 When They Call My NameRelea...

Japanese manga artist, screenwriter and film director Katsuhiro OtomoOtomo in 2016Born (1954-04-14) April 14, 1954 (age 70)Miyagi Prefecture, JapanNationalityJapaneseArea(s)Cartoonist, WriterNotable worksDōmuAkiraMetropolisSteamboyAwards Seiun Award (1982, 1984) Nihon SF Taisho Award (1983) Kodansha Manga Award (1984) Will Eisner Award (1992, 2002) Harvey Award (1993) Annie Award (2014) Grand Prix de la ville d'Angoulême (2015) Spouse(s)YokoChildrenShohei Otomo Katsuhiro Otomo (大友 ...

Yeovil Town 2002–03 football seasonYeovil Town2002–03 seasonChairmanJohn FryManagerGary JohnsonStadiumThe Avenue Stadium (Until September)Huish Park (From September)Conference1st (promoted)FA CupFirst roundFA TrophySixth roundFL TrophyFirst roundSomerset Premier CupRunners-upTop goalscorerLeague: Kirk Jackson (19)All: Kirk Jackson (20)Highest home attendance8,111 (26 April vs. Chester City, Conference, Huish Park)Lowest home attendance2,126 (21 September vs. Halifax Town, Conference, The...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. نينتندو إس-إس إم بي نينتندو إس-إس إم بي (بالإنجليزية: Nintendo S-SMP) هي وحدة المعالجة المركزية للصوت في جهاز الألعاب سوبر نينتندو إنترتينمنت سيستم. تتكون من معالج إشارة رقمي 16 بت و�...

Il governo Monti, gabinetto tecnico formato nel novembre 2011 a seguito della crisi del governo Berlusconi IV e degli effetti della congiuntura economica. Un governo tecnico, o anche governo dei tecnici,[1] è un tipo di governo dalla non dichiarata identità politica,[2][3] formato da personalità dotate di competenze tecniche specialistiche ed estranee alle forze politiche;[4] tale tipo di governo viene solitamente costituito in particolari situazioni in cui ...

Portable container that holds hygiene and toiletry supplies A clear plastic toiletry bag A toiletry bag (also called a toiletry kit, dopp kit, bathroom bag, ditty bag, sponge bag, toilet bag, personal hygiene kit, travel kit, or washkit) is a portable container—usually a pouch with a drawstring or zippered closure—that holds body hygiene and toiletry supplies such as toothbrush and toothpaste, dental floss, cotton swabs, deodorant, nail clippers, tweezers, soap, shaving supplies, hairbrus...

西維珍尼亞 美國联邦州State of West Virginia 州旗州徽綽號:豪华之州地图中高亮部分为西維珍尼亞坐标:37°10'N-40°40'N, 77°40'W-82°40'W国家 美國加入聯邦1863年6月20日(第35个加入联邦)首府(最大城市)查爾斯頓政府 • 州长(英语:List of Governors of {{{Name}}}]]) • 副州长(英语:List of lieutenant governors of {{{Name}}}]])吉姆·賈斯蒂斯(R)米奇·卡邁克爾(...

李光耀逝世及葬礼李光耀(1923年-2015年)日期2015年3月23日-2015年3月29日地点新加坡斯里淡马锡(私人守灵)新加坡国会大厦(民众瞻仰)新加坡国立大学文化中心(国葬)万礼火葬场(英语:Mandai Crematorium and Columbarium)(火葬)网站www.rememberingleekuanyew.sg 2015年3月23日凌晨3時18分(新加坡標準時間),新加坡建国后首任总理、前內閣资政和执政人民行动党首任秘书长李光�...

American company developing self-driving taxis Zoox, Inc.Company typeSubsidiaryIndustryAutomotiveFounded2014; 10 years ago (2014)FoundersTim Kentley-KlayJesse LevinsonHeadquartersFoster City, CaliforniaKey peopleAicha Evans (CEO)ProductsSelf-driving carsNumber of employeesc. 2,200 (2023)[1]ParentAmazon.com, Inc.Websitezoox.com Zoox, Inc. is a subsidiary of Amazon developing autonomous vehicles that provide mobility as a service. It is headquartered in Foster Ci...

Town in Massachusetts, United StatesAdamsTownHoosic River FlagSealLocation in Berkshire County and the state of Massachusetts.Coordinates: 42°37′27″N 73°07′05″W / 42.62417°N 73.11806°W / 42.62417; -73.11806CountryUnited StatesStateMassachusettsCountyBerkshireSettled1762Incorporated1778Government • TypeBoard of Selectmen Representative town meeting • Town AdministratorJay R. Green[1]Area • Total23.0 sq m...
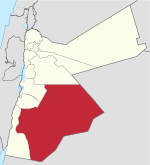
محطة الجرذانة - منطقة سكنية - تقسيم إداري البلد الأردن المحافظة محافظة معان لواء لواء قصبة معان قضاء قضاء معان السكان التعداد السكاني 214 نسمة (إحصاء 2015) • الذكور 112 • الإناث 102 • عدد الأسر 36 معلومات أخرى التوقيت ت ع م+02:00 تعديل مصدري - تعديل مح...

Planitia on Mars Amazonis PlanitiaTopographic map of Amazonis Planitia. MOLA colorized relief map of Amazonis Planitia. Colors indicate elevation, with red highest, yellow intermediate, and green/blue lowest.Coordinates24°48′N 196°00′E / 24.8°N 196.0°E / 24.8; 196.0 Amazonis Planitia (/əˈmæzənɪs pləˈnɪʃiə/, Latin Amāzŏnis) is one of the smoothest plains on Mars. It is located between the Tharsis and Elysium volcanic provinces, to the west of Olympus...

Calarcá Municipio Plaza de Bolívar de Calarcá. BanderaEscudo Otros nombres: Villa del Cacique, Cuna de Poetas CalarcáLocalización de Calarcá en Colombia CalarcáLocalización de Calarcá en QuindíoCoordenadas 4°31′45″N 75°38′27″O / 4.5291666666667, -75.640833333333Cabecera CalarcáEntidad Municipio • País Colombia • Departamento QuindíoAlcalde Juan Sebastián Ramos Velasco (2024-2027)Eventos históricos • Fundación 29 de ju...

Brazilian television presenter (1947–2023) Raimundo VarelaBornRaimundo Varella Freire Júnior30 November 1947 (1947-11-30)Itabuna, Bahia, BrazilDied7 September 2023 (2023-09-08) (aged 75)Salvador, Bahia, Brazil Raimundo Varella Freire Júnior (30 November 1947 – 7 September 2023), best known as Raimundo Varela, was a Brazilian television presenter. Life and career Born in Itabuna, as a child Varela moved with his family to Salvador.[1] Before starting his television...

Cet article est une ébauche concernant la Chine, l’archéologie, l’art et le bouddhisme. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Grottes de YulinPrésentationType Grotte ornementale, site archéologiquePatrimonialité Site national majeur (1961)LocalisationVille-préfecture JiuquanXian GuazhouCoordonnées 40° 03′ 33″ N, 95° 56′ 10″ Emodifier - modifier le...

Cet article est une ébauche concernant un cours d'eau de France et l’Essonne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article a besoin d’être illustré (en discuter) (décembre 2012). Pour améliorer cet article, des médias (images, animations, vidéos, sons) sous licence libre ou du domaine public sont les bienve...