|
|
ערך מחפש מקורות
|
רובו של ערך זה אינו כולל מקורות או הערות שוליים, וככל הנראה, הקיימים אינם מספקים.
אנא עזרו לשפר את אמינות הערך באמצעות הבאת מקורות לדברים ושילובם בגוף הערך בצורת קישורים חיצוניים והערות שוליים.
אם אתם סבורים כי ניתן להסיר את התבנית, ניתן לציין זאת בדף השיחה.
|
|
| ערך מחפש מקורות
|
רובו של ערך זה אינו כולל מקורות או הערות שוליים, וככל הנראה, הקיימים אינם מספקים.
אנא עזרו לשפר את אמינות הערך באמצעות הבאת מקורות לדברים ושילובם בגוף הערך בצורת קישורים חיצוניים והערות שוליים.
אם אתם סבורים כי ניתן להסיר את התבנית, ניתן לציין זאת בדף השיחה.
|
תאוריית האופטימליוּת או תאוריית המֵיטביוּת[1] (באנגלית: Optimality Theory; מקוצר לרוב כ-OT) היא מודל בלשני שלפיו הצורות הנצפות בשפות אנוש נובעות מיחסי גומלין בין עקרונות אוניברסליים הנקראים אילוצים. OT נבדלת ממודלים קודמים בכך שאינה משתמשת בחוקים ליניאריים הפועלים על פי סדר מסוים, ובמקום זאת ממדלת את הדקדוק כמערכת הממפה בפעולה אחת קלטים לפלטים, כאשר הקלט הוא באופן טיפוסי הייצוג המנטלי הבסיסי (Underlying Representation או UR) והפלטים הם מימושם בפועל.
התאוריה פותחה במקור על ידי הבלשנים אלן פרינס ופול סמולנסקי בשנת 1993[2], ולאחר מכן הורחבה על ידי פרינס וג'ון ג'. מקארתי. אף שרוב שימושיה הם בתחום הפונולוגי ניתן להחילה גם בתחומים אחרים במחקר הבלשני, כגון תחביר וסמנטיקה. בדומה ליתר התאוריות הגנרטיביות, גם OT מתמקדת בעקרונות אוניברסליים ויש לה עניין בטיפולוגיה של שפות ובתהליך רכישתן.
מבנה התאוריה
התאוריה מחלקת את הדקדוק לשלושה רכיבים:
- GEN, Generator - מחולל
- CON, Constraints - אילוצים
- EVAL, Evaluator - מעריך
רכיבים אלה מונחים כאוניברסליים, וההבדלים בין הדקדוקים השונים בפועל מוסברים באמצעות הבדלים בדירוגים של האילוצים מתוך CON. את תהליך רכישת השפה ניתן לתאר ככוונון מתמשך של דירוג האילוצים.
GEN: סט המועמדים
תאוריית האופטימליות מניחה שאין אילוצים או מגבלות כלשהם על הקלט הלשוני. עיקרון זה, הנקרא גם עושר הבסיס, משמעו שכל דקדוק חייב להיות מסוגל להתמודד עם כל קלט שהוא. לדוגמה, שפה שאין בה צרורות עיצורים חייבת להיות מסוגלת להתמודד עמם, ושפות שונות שבהן אין צרורות עיצורים יפתרו את הבעיה באחת משתי דרכים שונות: החדרת תנועה (אפנתזיס) או מחיקת עיצור. למשל, הקלט האפשרי /flask/ המכיל שני צרורות עיצורים, יעבור בשפות אלה החדרה או מחיקה כדי ליצור כל אחד מהפלטים האפשריים [falasak], [fak], [fas], [lak], [las] או אחרים (למשל, אם צרורות מותרים בעמדות מסוימות בהברה ואסורים באחרות, וכו'). התאוריה מניחה שבהינתן כל קלט GEN מייצר אינסוף מועמדים (כולל שרירותיים לחלוטין), ותפקידו של EVAL לבחור את האופטימלי ביניהם בהתאם לדירוג האילוצים מתוך CON.
CON: סט האילוצים
על פי תאוריית האופטימליות כל האילוצים אוניברסליים (כלומר קיימים בכל שפות האנוש). קיימים שני סוגים בסיסיים של אילוצים: אילוצי נאמנות, הדורשים שהצורה הנצפית על פני השטח תהיה תואמת לקלט (שהוא הייצוג המנטלי), ואילוצי מסומננות, המציבים הגבלות על מבנה הפלט וקובעים הלכה למעשה מה נחשב לפלט תקין בשפה. שני סוגי האילוצים הם ברי הפרה, כלומר עצם העובדה שפלט מסוים מפר אותם לא בהכרח פוסלת אותו מלהיבחר כאופטימלי ולהתבצע בפועל על ידי הדוברים.
מטיבו האוניברסלי של CON ניתן לנסח ניבויים באשר לטיפולוגיה של שפות. אם ההבדל היחידי בין דקדוקים הוא הדירוגים השונים של אילוצים מתוך CON, אז קבוצת כל שפות האנוש הקיימות מוגבלת בגודלה על ידי מספר האילוצים - הניבוי הוא שמספר השפות לא יכול להיות גדול ממספר הפרמוטציות האפשריות של הדירוג; אם כן, מדובר בטיפולוגיה פקטוריאלית (מלשון Factorial, עצרת באנגלית). אולם, לא בהכרח ניתן להבחין בין כל הדקדוקים הפוטנציאליים האלו, משום שלא לכל אילוץ תפקיד נראה לעין בכל דקדוק - שתי שפות יכולות לייצר את אותו סט של מיפויי קלטים לפלטים, אבל להיבדל בדירוג של שני אילוצים שאינם נמצאים בתחרות זה עם זה.
EVAL: הגדרת האופטימליות
בהינתן שני מועמדים לפלט A ו-B, המועמד A עדיף על B ביחס לאילוץ מסוים אם A מפר את האילוץ פחות פעמים מש-B מפר אותו. מועמד A עדיף מ-B לאורך כל היררכיית האילוצים אם A מפר פחות פעמים מ-B את האילוץ הגבוה ביותר בדירוג שמבדיל בין A ל-B (כלומר, שמספר ההפרות שלהם אותו שונה). A הוא מועמד אופטימלי אם הוא מועמד עדיף על כל המועמדים האחרים בסט לאורך כל היררכיית האילוצים. לדוגמה, בהינתן האילוצים C1, C2, C3, כאשר C1 מדורג מעל (או "שולט" על) C2 שמדורג מעל C3, המועמד A אופטימלי אם הוא עדיף על מועמד B ביחס לאילוץ הגבוה ביותר בדירוג שמעניק לשניהם מספר שונה של הפרות. דהיינו, אם מתקיים תיקו בין A ל-B ביחס ל-C1, אבל A עדיף מ-B ביחס ל-C2, מועמד A אופטימלי, ואין זה משנה אם הוא מפר את C3 (הנמוך בדירוג) גם מאה פעמים יותר מש-B מפר אותו. השוואות אלה מודגמות באמצעות טבלה, הנקראת לרוב טאבּלוֹ (מצרפתית, Tableau), כמו זו המצורפת מטה. סמליל האצבע מציין את המועמד האופטימלי, וכל כוכבית מציינת הפרה של האילוץ בראש הטור על ידי המועמד שבתחילת השורה. ברגע שמועמד מסוים אינו עדיף על אף מועמד ביחס לאילוץ הגבוה ביותר בדירוג המבחין בינו לבין מועמדים אחרים, מדובר בהפרה הנקראת פטאלית, שמסומנת בסימן קריאה ומשמעה שמועמד זה לא יכול להיות אופטימלי, גם אם הוא עדיף ביחס לאילוצים נמוכים יותר בדירוג.

האילוצים מדורגים בהיררכיית שליטה נוקשה. משמעה של נוקשות זו היא שמועמד המפר אילוץ שמדורג גבוה תמיד יחשב לגרוע יותר גם ממועמד שמפר את כל האילוצים המדורגים נמוך יותר. כמו כן, ההיררכיה מדגימה את ההנחה שהאילוצים הם, כאמור, תמיד ברי הפרה - המועמד האופטימלי לא מחויב שלא להפר אף אילוץ אלא רק למספר המינימלי ביותר של ההפרות ובהתאם להיררכיה. בתוך שפה נתונה, ייתכן שאילוץ יהיה מדורג גבוה מספיק כדי שהפלט תמיד יציית לו, ייתכן שהוא ידורג נמוך מספיק כדי שלא תהיה לו השפעה נראית לעין, וייתכן שיהיה מדורג היכנשהו באמצע. המונח הגחת הבלתי מסומנן (מאנגלית, Emergence of the Unmarked) מתאר מצבים שבהם אילוץ מסומננות כלשהו נמצא במקום אמצעי יחסית בדירוג, מה שגורם להפרתו במקרים מסוים אבל עדיין מאפשר לראות את השפעתו על הפלט כאשר האילוצים המדורגים מעליו אינם רלוונטיים להכרעת הדירוג.
ישנם בלשנים המעדיפים שימוש בטאבלו השוואתיות, שהוצעו על ידי פרינס במאמרו משנת 2002. אלה מציגות את אותו המידע כמו בטאבלו הקלאסיות, אך מדגישות את המידע החיוני. למשל, הטבלה הקודמת תוצג בצורה הבאה:
כל שורה בטאבלו מייצג זוג של מועמד מנצח ומועמד מפסיד, בניגוד לטבלה המסורתית המאפשרת שורה למועמדים אינדיבידואליים. עבור כל אילוץ מצוין אם אותו אילוץ מעדיף את המנצח (W), המפסיד (L), או אם האילוץ אינו מבחין בין שני המועמדים (e). הצגת המידע באופן הזה עשויה להקל על הגעה להכללות.
דוגמה
כדוגמה פשוטה יחסית ליישום התאוריה ניתן לקחת את מבנה צורת הרבים באנגלית. באופן בסיסי הניתוח הבלשני המודרני המקובל הוא שמורפמת הריבוי באנגלית היא /z/, כאשר קיימים שלושה מימושים אפשריים שלה: [z] [s] ו-[ɨz].
האילוצים הרלוונטיים לסט הנתונים, בסדר הדירוג:
- מסומננות:
- SS* - איסור על צרור של עיצורים שורקים, הפרה אחת מסומנת על כל זוג שורקים בפלט.
- Agree(Voi) - התאמה בקוליות, הפרה אחת על כל זוג עיצורים לא סונורנטים שאינם תואמים בקוליות שלהם.
- נאמנות:
- Max - מקסימיזציה של הגאי הקלט (איסור על מחיקה בפלט), הפרה על כל הגה מהקלט שאינו נמצא בפלט.
- Dep - תלות בהגאי הקלט (איסור על החדרת הגאים לפלט), הפרה על כל הגה מהפלט שאינו נמצא בקלט.
- Ident(Voi) - זהות בקוליות, הפרה על כל הבדל בקוליות עיצורים בין הקלט לפלט.
dish + z > dishiz
| dish + z
|
*SS
|
Agree
|
Max
|
Dep
|
Ident
|
| ☞ dishiz
|
|
|
|
*
|
|
| dishis
|
|
|
|
*
|
*!
|
| dishz
|
*!
|
*
|
|
|
|
| dish
|
|
|
*!
|
|
|
| dishs
|
*!
|
|
|
|
*
|
dog + z > dogz
| dog + z
|
*SS
|
Agree
|
Max
|
Dep
|
Ident
|
| dogiz
|
|
|
|
*!
|
|
| dogis
|
|
|
|
*!
|
*
|
| ☞ dogz
|
|
|
|
|
|
| dog
|
|
|
*!
|
|
|
| dogs
|
|
*!
|
|
|
*
|
cat + z > cats
| cat + z
|
*SS
|
Agree
|
Max
|
Dep
|
Ident
|
| catiz
|
|
|
|
*!
|
|
| catis
|
|
|
|
*!
|
*
|
| catz
|
|
*!
|
|
|
|
| cat
|
|
|
*!
|
|
|
| ☞ cats
|
|
|
|
|
*
|
לא משנה כיצד נסדר מחדש את האילוצים, האלומורף (כלומר החלופה המורפולוגית) [is-] תמיד תפסיד. מצב זה נקרא כבילה הרמונית (Harmonic Binding): ההפרות של המועמד dogiz הן תת-קבוצה של ההפרות של המועמד dogis, כך שהראשון תמיד יהיה עדיף. באותה הטאבלו, המועמד האופטימלי dogz למעשה כובל הרמונית את כל יתר המועמדים.
בהתבסס על הטאבלו הנ"ל ניתן להגיע לשני דירוגי אילוצים:
*SS, Max >> Agree, Dep >> Ident
או:
*SS, Max, Agree >> Dep >> Ident
עם זאת, כתיבת הדירוג באופן ליניארי אינה מדויק משום שמשתמעים ממנה דירוגים שאינם מחויבי המציאות על פי הניתוח. לכן לרוב משתמשים בדיאגרמת עץ כדי לייצג את הדירוג, למשל:
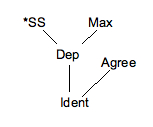
ביקורת
תאוריית האופטימליות הייתה ועודנה נתונה לביקורת משמעותית.
בלשנים מסוימים טוענים כי התאוריה לא מצליחה להסביר תופעות פונולוגיות מסוג Opacity. בפונולוגיה של מילים נגזרות נראה לעיתים שיש צורות שלא ניתן להסבירן אלא באמצעות סדר חוקים ליניארי שאינו נראה על פני השטח, אך בתאוריית האופטימליות אין שלבי ביניים (כל האילוצים פועלים באותה הרמה), מה שמקשה על מתן הסבר.
למשל, בצרפתית של קוויבק תנועות גבוהות וקדמיות גורמות לאפריקציה של /t/ (למשל: /tipik/ המבוצע [tˢpɪk]), אבל אובדן התנועה הגבוהה על פני השטח מותיר את התופעה ללא הסבר נראה לעין. בסדר חוקים ליניארי ניתן לומר שהתקיים סדר חוקים מסוג counterbleeding; האפריקציה מתרחשת לפני השמטת התנועה ולכן היא עדיין מוסברת על ידי הימצאותה בצורה המקורית. זאת בניגוד לסדר מסוג bleeding שמתקיים במקרה שההשמטה מתרחשת לפני שהאפריקציה יכולה להתרחש ומותירה אותה, תאורטית, ללא הסבר. מצב של counterbleeding נקרא בלתי שקוף (opaque) משום שההשפעות שלו לא נראות מיידית על פני השטח. לתופעה זו אין הסבר ישיר במסגרת OT, וההצעות לפתרון מצריכות שינויים מבניים גדולים ומעוררי במחלוקת בעקרונות הבסיסיים של התאוריה.
כמו כן קיימת ביקורת על המופרכות החישובית של OT כמודל להפקה ותפיסה של דיבור, שכן יצירת והערכת אינסוף מועמדים אפשריים תיקח פרק זמן אינסופי באותה המידה. טענה נגדית לביקורת זו מדגישות ש-OT היא מודל ייצוגי בלבד המהווה מודל לכשירות לשונית ולא מותאמת להסביר את דקויות הביצוע הלשוני.
התנגדות נוספת, המשותפת למתנגדים לתאוריות גנרטיביות אחרות, היא על עצם השימוש במונח "תאוריה", שכן יש הטוענים ש-OT איננה מציעה ניבויים בני הפרכה. עם זאת ניתן לטעון שמודלים פרטניים במסגרת OT יכולים להציע ניבויים ברי הפרכה, כמו במסגרות תאורטיות בלשניות אחרות. אופיים של הניבויים והמידה בה ניתן לבחון אותם תלויים במאפיינים הפרטניים של המודלים (לרוב, מדובר בהגדרות האילוצים). אי לכך ניתן להגדיר את תאוריית האופטימליות כפרדיגמה מדעית.
קישורים חיצוניים
הערות שוליים