ОЕОЎОўОф ОъОўОбОаОЎ ОЊОъОЋОф
|
Read other articles:

пД┘ёп╣┘ёпД┘ѓпДпф пД┘ёпБ┘єп»┘ѕп▒┘іпЕ пД┘ёп▒┘ѕпД┘єп»┘іпЕ пБ┘єп»┘ѕп▒пД п▒┘ѕпД┘єп»пД пБ┘єп»┘ѕп▒пД п▒┘ѕпД┘єп»пД пфп╣п»┘і┘ё ┘Ёпхп»п▒┘і - пфп╣п»┘і┘ё пД┘ёп╣┘ёпД┘ѓпДпф пД┘ёпБ┘єп»┘ѕп▒┘іпЕ пД┘ёп▒┘ѕпД┘єп»┘іпЕ ┘Є┘і пД┘ёп╣┘ёпД┘ѓпДпф пД┘ёпФ┘єпДпд┘іпЕ пД┘ёпф┘і пфпг┘Ёп╣ пе┘і┘є пБ┘єп»┘ѕп▒пД ┘ѕп▒┘ѕпД┘єп»пД.[1][2][3][4][5] ┘Ё┘ѓпДп▒┘єпЕ пе┘і┘є пД┘ёпе┘ёп»┘і┘є ┘Єп░┘Є ┘Ё┘ѓпДп▒┘єпЕ п╣пД┘ЁпЕ ┘ѕ┘Ёп▒пгп╣┘іпЕ ┘ё┘ёп»┘ѕ┘ёпф┘і┘є: ┘ѕпг┘Є пД┘ё┘Ё┘ѓпДп▒┘єпЕ...

Adolfo Geri Adolfo Geri (Napoli, 28 agosto 1912 РђЊ Roma, 27 marzo 1988) ├е stato un attore e doppiatore italiano. Indice 1 Biografia 2 Doppiaggio 3 Prosa radiofonica 4 Prosa televisiva RAI 5 Filmografia 6 Bibliografia 7 Altri progetti 8 Collegamenti esterni Biografia Nato a Napoli da una famiglia di attori inizia a recitare sin da bambino in teatro e successivamente nel cinema, dove debutta nel 1933, nel film L'eredit├а dello zio buonanima, diretto da Amleto Palermi. Nel 1938 entra all'inter...

Cet article est une ├Еbauche concernant un groupe de musique. Vous pouvez partager vos connaissances en lРђЎam├Еliorant (comment ?) selon les recommandations des projets correspondants. Klapa s Mora L'ensemble sur la sc├еne de l'Eurovision en 2013.Informations g├Еn├Еrales Pays d'origine Croatie Genre musical Klapa, musique classique Ann├Еes actives Depuis 2013 Composition du groupe Membres Marko ┼аkugorAnte Gali─ЄNik┼Аa AnticaLeon BataljakuIvica Vlai─ЄBojan Kaved┼Йija modifier Klapa s M...
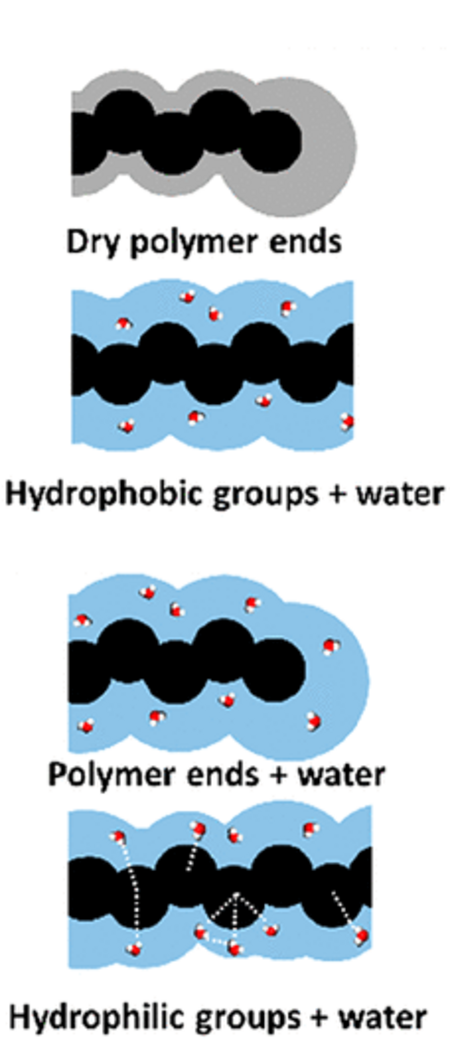
In polymer chemistry and polymer physics, the FloryРђЊFox equation is a simple empirical formula that relates molecular weight to the glass transition temperature of a polymer system. The equation was first proposed in 1950 by Paul J. Flory and Thomas G. Fox while at Cornell University.[1] Their work on the subject overturned the previously held theory that the glass transition temperature was the temperature at which viscosity reached a maximum. Instead, they demonstrated that the gl...

Swedish-American actor (1879РђЊ1938) Warner OlandOland in 1919BornJohan Verner ├ќlund(1879-10-03)October 3, 1879Nyby, Bjurholm Municipality, SwedenDiedAugust 6, 1938(1938-08-06) (aged 58)Stockholm, SwedenResting placeSouthborough Rural Cemetery, Southborough, Massachusetts, USOccupationActorYears active1902–1937Known forCharlie ChanSpouse Edith Gardener Shearn (m. 1907–1938) Warner Oland (born Johan Verner ├ќlun...

лБ ЛЇЛѓлЙл│лЙ ЛѓлхЛђл╝лИлйл░ ЛЂЛЃЛЅлхЛЂЛѓл▓ЛЃЛјЛѓ лИ л┤ЛђЛЃл│лИлх лилйл░ЛЄлхлйлИЛЈ, ЛЂл╝. лЌл░л┐л░л┤лйЛІл╣ лЙл║ЛђЛЃл│. лЌл░л┐л░л┤лйЛІл╣ л▓лйЛЃЛѓЛђлИл│лЙЛђлЙл┤ЛЂл║лЙл╣ лЙл║ЛђЛЃл│ л│лЙЛђлЙл┤ лџЛђл░ЛЂлйлЙл┤л░Лђ лћл░Лѓл░ лЙЛЂлйлЙл▓л░лйлИЛЈ 1936 л│лЙл┤ лћл░Лѓл░ ЛЃл┐Лђл░лил┤лйлхлйлИЛЈ 1994 лЪЛђлхлХлйлИлх лИл╝лхлйл░ лџл░л│л░лйлЙл▓лИЛЄЛЂл║лИл╣, лЏлхлйлИлйЛЂл║лИл╣ Лђл░л╣лЙлйЛІ люлИл║ЛђлЙЛђл░л╣лЙлйЛІ лћЛЃл▒лИлйл║л░, лДлхЛђЛЉл╝ЛЃЛѕл║лИ, лЪлЙл║ЛђлЙл▓л║л░ лЪл╗лЙЛЅл░л┤Лї 22[1] л║л╝┬▓ лЮл░ЛЂлх...

Ploaghe Pi├аgheKomuneComune di PloagheLokasi Ploaghe di Provinsi SassariNegaraItaliaWilayah SardiniaProvinsiSassari (SS)Pemerintahan Рђб Wali kotaCarlo SotgiuLuas Рђб Total96,27 km2 (37,17 sq mi)Ketinggian427 m (1,401 ft)Populasi (2016) Рђб Total4,538[1]Zona waktuUTC+1 (CET) Рђб Musim panas (DST)UTC+2 (CEST)Kode pos07017Kode area telepon079Situs webhttp://www.comune.ploaghe.ss.it Ploaghe (bahasa Sardinia: Pi├аghe) a...

SenateDominion of CeylonTypeTypeUpper house HistoryEstablished1947Disbanded2 October 1971Preceded byState Council of CeylonSucceeded byNoneSeats30Meeting placeThe old Legislative Council building in Colombo Fort that used to house the Senate. Today it is known as the Republic Building and houses the Ministry of Foreign Affairs. Politics of Sri Lanka Constitution Previous constitutions: 1931 ┬и 1947 Law of Sri Lanka Human rights Law enforcement GovernmentExecutive President (List) Pr...

Part of a series on: Kurdish history and Kurdish culture People List of Kurds Population Homeland Kurdistan Turkey (Northern Kurdistan) Iran (Eastern Kurdistan) Iraq (Southern Kurdistan) Syria (Western Kurdistan) Diaspora Armenia Australia Azerbaijan Belgium Canada Czech Republic Denmark Finland France Georgia Germany Greece Iraq Iran Ireland Israel Japan Jordan Kazakhstan Lebanon Netherlands New Zealand Norway Palestine Pakistan Romania Russia Syria Sweden Turkmenistan Turkey Ukraine ...

The Traffic in Women: Notes on the Political Economy of Sex is an article regarding theories of the oppression of women originally published in 1975 by feminist anthropologist Gayle Rubin.[1] In the article, Rubin argued against the Marxist conceptions of women's oppressionРђћspecifically the concept of patriarchyРђћin favor of her own concept of the sex/gender system.[2][3] It was by arguing that women's oppression could not be explained by capitalism alone as well as...

┘ё┘Ёп╣пД┘є┘Ї пБп«п▒┘Ѕпї пипД┘ёп╣ пг┘ѕп▒пг пбп▒пФп▒ (пф┘ѕпХ┘іпГ). пг┘ѕп▒пг пбп▒пФп▒ ┘Ёп╣┘ё┘ѕ┘ЁпДпф п┤п«пх┘іпЕ пД┘ё┘Ё┘і┘ёпДп» 30 ┘і┘ѕ┘є┘і┘ѕ 1968(1968-06-30)п│┘ѕ┘є┘іпДпф┘і пД┘ё┘ѕ┘ЂпДпЕ 14 ┘і┘ѕ┘є┘і┘ѕ 2015 (п╣┘є п╣┘Ёп▒ ┘єпД┘Єп▓ 46 п╣пД┘ЁпД┘І)п│┘ѕ┘є┘іпДпф┘і ┘Ёп▒┘Ѓп▓ пД┘ё┘ёп╣пе ┘Ё┘ЄпДпг┘Ё пД┘ёпг┘єп│┘іпЕ п║пД┘єпД пД┘ё┘Ёп│┘іп▒пЕ пД┘ёпДпГпфп▒пД┘Ђ┘іпЕ1 п│┘є┘ѕпДпф ┘Ђп▒┘і┘ѓ ┘Ё. (┘Є┘ђ.) 1982РђЊ1983 BA Stars F.C. [пД┘ёпЦ┘єпг┘ё┘іп▓┘іпЕ] 1984РђЊ1987 пБп┤пД┘...

Barbra Streisand Barbra Streisand Nome completo Barbara Joan Streisand Nascimento 24 de abril de 1942 (82 anos)Brooklyn, Nova IorqueEstados Unidos Ocupa├Д├Бo atriz, diretora, produtora e cantora Atividade 1960РђЊpresente C├┤njuge Elliott Gould (c. 1963; div. 1971)James Brolin (c. 1998) Filho(a)(s) Jason Gould Oscares da Academia Melhor Atriz Principal1969 - Funny GirlMelhor Can├Д├Бo Original1977 - A Star Is Born Emmys Melhor Realiza├Д├Бo Individual19...

Australian TV network This article is about the Australian television network. For the network's flagship station, see WIN (TV station). For other television networks called WIN, see WIN TV. Television channel WIN TelevisionCountryAustraliaBroadcast areaRegional Queensland, Northern NSW & Gold Coast, Southern NSW & ACT, Griffith, Regional Victoria, Mildura, Tasmania, Eastern SA, Regional WAAffiliatesNine NetworkSeven Network (Griffith and Eastern SA)Network 10 (Gold Coast, Northern NS...

Burnie BurnieBurnieтЮљТаЄ№╝џ41┬░03Рђ▓49Рђ│S 145┬░53Рђ▓31Рђ│E / 41.063611111111┬░S 145.89194444444┬░E / -41.063611111111; 145.89194444444тЏйт«Х ТЙ│тцДтѕЕС║ъСИђу║ДУАїТћ┐тї║тАћТќ»ждгт░╝С║ътиътю░Тќ╣Тћ┐т║ютї║тЪЪCity of BurnieС║║тЈБ Рђб уИйУеѕ19,030 (2,004)[1]С║║ТЌХтї║AEST№╝ѕUTC+10№╝Ѕ Рђб тцЈТЌХтѕХAEDT№╝ѕUTC+11№╝ЅСйЇуй«47тЁгжЄї№╝ѕ29УІ▒жЄї№╝Ѕ134тЁгжЄї№╝ѕ83УІ▒жЄї№╝Ѕ154тЁгжЄї№╝ѕ96УІ▒жЄї№╝Ѕ296тЁгжЄї№╝ѕ184УІ▒жЄї№╝ЅтиъжЂИтЇђBraddonУЂ»жѓджЂИтЇђBraddon С╝»у...

Ruling party of Burma from 1962 to 1988 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Burma Socialist Programme Party РђЊ news ┬и newspapers ┬и books ┬и scholar ┬и JSTOR (June 2012) (Learn how and when to remove this message) Burma Socialist Programme Party рђЎрђ╝рђћрђ║рђЎрђгрђирђєрђГрђ»рђЏрђЙрђџрђ║рђюрђЁрђ║рђюр...

Voce principale: Il Giallo Mondadori. I 100 precedenti: Il Giallo Mondadori dal 401 al 500 Dal N.501 al N.600 N. Titolo italiano Autore Titolo originale Pubblicazione 501 Terra maligna Helen Nielsen Stranger In The Dark 7 settembre 1958 502 ...chi ride ultimo A. A. Fair You Can Die Laughing 14 settembre 1958 503 Una tomba piena di soldi Bruno Fischer The Hornet's Nest 21 settembre 1958 504 Coscienza sporca Vernon Warren The Blue Mauritius 28 settembre 1958 505 Non fidarsi ├е meglio A.E. Mart...

Artikel ini bukan mengenai Vyacheslav Gryaznov. Vyacheslav Glazkoveлњ'ЛЈЛЄлхЛЂл╗л░л▓ лЊл╗л░лил║лЙл▓StatistikNama asliVyacheslav ValerЛќyovich GlazkovNama panggilanThe CzarDinilai padaHeavyweightTinggi1.88 mMencapai192 cmLahir15 Oktober 1984 (umur 39)Luhansk, Republik Sosialis Soviet Ukraina, Uni Soviet (Sekarang Ukraina)SikapOrthodoxCatatan tinjuTotal perkelahian23Menang21Menang oleh KO13Kalah1Imbang1 Rekam medali Men's boxing Mewakili Ukraina Olympic Games 2008 Beijing Super heavy...

Disambiguazione РђЊ Se stai cercando altri significati, vedi Nero Wolfe (disambigua). Nero WolfeTino Buazzelli nei panni di Nero Wolfe nell'omonimo sceneggiato RAI UniversoNero Wolfe Nome orig.Nero Wolfe Lingua orig.Americano AutoreRex Stout EditoreViking Press 1ª app.24 ottobre 1934 1ª app. inLa traccia del serpente Editore it.Arnoldo Mondadori Editore Caratteristiche immaginarieSessoMaschio Luogo di nascitaimpreciso (Trenton (New Jersey) o Montenegro) Data di nascitaSco...

Georgian general, born and served in Russia (1765РђЊ1812) For the royal dynasty, see Bagrationi dynasty. In this name that follows Eastern Slavic naming customs, the patronymic is Ivanovich and the family name is Bagration. General PrincePyotr Ivanovich BagrationPortrait by George DaweNative nameрЃърЃћрЃбрЃарЃћ рЃЉрЃљрЃњрЃарЃљрЃбрЃўрЃЮрЃюрЃўNickname(s)God of the Army[1]The Eagle[citation needed]Born(1765-07-10)10 July 1765Kizlyar,[2] Astrakhan Governorate, Russian...

Der Titel dieses Artikels ist mehrdeutig. Weitere Bedeutungen sind unter Samoa (Begriffskl├цrung) aufgef├╝hrt. Unabh├цngiger Staat Samoa M─Ђl┼Ї Sa╩╗oloto T┼Фto╩╗atasi o S─Ђmoa (samoanisch)Independent State of Samoa (englisch) Flagge Wappen Wahlspruch: Fa╩╗avae i le Atua S─ЂmoaРђъSamoa ist gegr├╝ndet auf GottРђю Amtssprache Samoanisch und Englisch Hauptstadt Apia Staats- und Regierungsform parlamentarische Republik Staatsoberhaupt O le Ao o le M─Ђl┼Ї Va╩╗aletoa Sualauvi II. Regierungschef Pre...
























