ניתוח תדירויות
|
Read other articles:

BetterHelpJenisAnak perusahaanIndustriPsikoterapiDidirikan2013; 11 tahun lalu (2013)PendiriAlon MatasDanny BragonierKantorpusatMountain View, California, ASWilayah operasiSeluruh duniaJasaTerapi online Terapi perpesanan tanpa batasIndukTeladoc HealthSitus webwww.betterhelp.com BetterHelp adalah platform kesehatan mental yang menyediakan layanan kesehatan mental daring langsung kepada konsumen. Layanan konseling dan terapi daring disediakan melalui interaksi berbasis web serta komunikasi ...

Licuala Licuala grandis Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Monokotil (tanpa takson): Commelinids Ordo: Arecales Famili: Arecaceae Subfamili: Coryphoideae Tribus: Corypheae Genus: LicualaWurmb, 1780 Spesies Lihat teks Licuala merupakan kelompok tumbuhan monokotil berkayu. Licuala merupakan marga palem yang terdiri dari 130 jenis, salah satu jenis Licuala ini adalah Licuala paludosa Griff. ex Mart. Jenis yang familiar di masyarakat Indonesia adala...

British political economist (1766–1834) Malthus redirects here. For the demon Halphas, sometimes called Malthus, see Halphas. The ReverendThomas Robert MalthusFRSMalthus in 1834Born13/14 February 1766Westcott, Surrey, EnglandDied29 December 1834(1834-12-29) (aged 68)Bath, Somerset, EnglandEducationJesus College, Cambridge (MA)Spouse Harriet Eckersall (m. 1804)Children3Academic careerFieldDemographymacroeconomicsSchool ortraditionClassical economicsIn...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (November 2022) Edward BlondinBornDélı̨nę[1][2]Occupation(s)shaman, hunter, surveyor, lumberjackSpouseEliza Blondin[2] Edward Blondin was a member of the Sahtu Dene First Nation, who played a prominent role in the industrial development of Canada's north.[3][4][5][6] CBC News q...

Division of the Tamil Nadu Police Greater Chennai PoliceLogo of the Greater Chennai PoliceCommon nameChennai PoliceMottoTruth alone triumphsAgency overviewFormed1659Preceding agencyChennai Suburban Police Chennai City PoliceEmployees23625Jurisdictional structureOperations jurisdictionChennai, Tamil Nadu, IndiaGoverning bodyDepartment of Home, Government of Tamil NaduGeneral natureLocal civilian policeOperational structureHeadquartersChennai Police CommissionerateElected officer responsib...

American baseball player (1874–1959) Baseball player Frank HuelsmanLeft fielderBorn: (1874-06-05)June 5, 1874St. Louis, Missouri, U.S.Died: June 9, 1959(1959-06-09) (aged 85)Affton, Missouri, U.S.Batted: RightThrew: RightMLB debutOctober 3, 1897, for the St. Louis BrownsLast MLB appearanceOctober 5, 1905, for the Washington SenatorsMLB statisticsBatting average.258Home runs5Runs batted in97 Teams St. Louis Browns (1897) Chicago White Sox (1904) Detroit Tig...

Cet article est une ébauche concernant un astronaute américain. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Richard Linnehan Nationalité Américain Sélection Groupe 14 de la NASA, 1992 Naissance 19 septembre 1957 (66 ans)Lowell, Massachusetts Durée cumulée des missions 59 j 20 h 49 min Mission(s) STS-78STS-90STS-109STS-123 Insigne(s) modifier Richard Michael Linnehan est un astronaute ...

Indian politician Haribhai Parthibhai ChaudharyMinister of state for CoalIn office3 September 2017 – 30 May 2019Prime MinisterNarendra ModiMinisterPiyush GoyalMinister of state for MinesIn office3 September 2017 – 30 May 2019Prime MinisterNarendra ModiMinisterNarendra Singh TomarMinister of state for Micro, Small & Medium EnterprisesIn office5 July 2016 – 3 September 2017Prime MinisterNarendra ModiMinisterKalraj MishraMinister of state for Home AffairsIn o...

Disambiguazione – Se stai cercando altri significati, vedi Indipendentismo (disambigua). Questa voce sull'argomento politica è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. L'indipendentismo è il fenomeno politico caratterizzato dal rivendicare l'indipendenza di un territorio dalla sovranità di uno Stato; spesso si usa anche il termine separatismo o secessionismo. Può essere di matrice ideologica,...

沙丘Dune電影海報基本资料导演丹尼·維勒納夫监制 凱爾·波伊特 瑪麗·帕倫(英语:Mary Parent) 丹尼·維勒納夫 编剧 艾瑞克·羅斯 丹尼·維勒納夫 喬·斯派茨 原著《沙丘》法蘭克·赫伯特作品主演 提摩西·夏勒梅 蕾貝卡·弗格森 奧斯卡·伊薩克 喬許·布洛林 史戴倫·史柯斯嘉 巴帝斯塔 史蒂芬·亨德森(英语:Stephen Henderson (actor)) 赞达亚 戴維·達斯馬齊連(英语:David Dastmal...

نادي القارة السعودي الاسم الكامل نادي القارة لكرة القدم الألوان السماوي و الأبيض تأسس عام 1972 م - 1391 هـ الملعب الأحساء (محافظة) السعودية البلد السعودية الدوري دوري الدرجة الثالثة السعودي 2020-2021 2020-2021 الإدارة المالك الهيئة العامة للرياضة الأستاذ عادل[1] الطقم الأسا�...

Scottish philosopher and ethicist (born 1987) William MacAskillMacAskill in 2015BornWilliam David Crouch (1987-03-24) 24 March 1987 (age 37)Glasgow, ScotlandEducation Jesus College, Cambridge (BA, 2008) St Edmund Hall, Oxford (BPhil, 2010) St Anne's College, Oxford (DPhil, 2014) Spouse Amanda Askell (divorced)[1]EraContemporary philosophyRegionWestern philosophyInstitutions Emmanuel College, Cambridge Lincoln College, Oxford Global Priorities Institute T...

Japanese physicist Yoshio Nishina仁科 芳雄Born(1890-12-06)December 6, 1890Satoshō, OkayamaDiedJanuary 10, 1951(1951-01-10) (aged 60)NationalityJapaneseKnown forKlein–Nishina formulaAwardsAsahi Prize (1944) Order of Culture (1946)Scientific careerFieldsPhysicsInstitutionsRIKENNotable studentsHideki Yukawa Sin-Itiro Tomonaga Shoichi Sakata Yoshio Nishina (仁科 芳雄, Nishina Yoshio, December 6, 1890 – January 10, 1951) was a Japanese physicist who was called the founding f...

Julio Bárbaro Vicepresidente segundo interventor del Partido Justicialista 10 de abril de 2018-2 de agosto de 2018Presidente Luis Barrionuevo Director Ejecutivo del Comité Federal de Radiodifusión 10 de junio de 2003-31 de marzo de 2008Presidente Néstor Kirchner (2003-2007) Cristina Fernández de Kirchner (2007-2008)Predecesor Carlos CaterbettiSucesor Gabriel Mariotto (como interventor) Secretario de Cultura de la Nación Argentina 8 de julio de 1989-18 de marzo de 1991[1]President...

Dohaالدوحة Plaats in Qatar Coördinaten 25°18'NB, 51°32'OL Algemeen Oppervlakte 132 km² Inwoners (2010) 796.947[1] Overig Tijdzone UTC+3 Website Officiële website Foto's Universiteit van Qatar - Museum voor Islamitische Kunst Doha Corniche Waqif Soek - The Pearl Luchtfoto Portaal Azië Doha (Arabisch: الدوحة, ad-doha of ad-dawhah, letterlijk: de grote boom) is de hoofdstad van Qatar en de volkrijkste gemeente van het land. De stad heeft ongeveer 800....

Sunni Islamist political party in Lebanon This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs to be updated. Please help update this article to reflect recent events or newly available information. (May 2022) You can help expand this article with text translated from the corresponding article in Arabic. Click [show] for important translation instructions. Machine translatio...

Place in Upper Carniola, SloveniaMlaka pri KranjuMlaka pri KranjuLocation in SloveniaCoordinates: 46°16′26.63″N 14°20′50.92″E / 46.2740639°N 14.3474778°E / 46.2740639; 14.3474778Country SloveniaTraditional regionUpper CarniolaStatistical regionUpper CarniolaMunicipalityKranjArea • Total2.22 km2 (0.86 sq mi)Elevation416.1 m (1,365.2 ft)Population (2002) • Total1,502[1] Mlaka pri Kranju (pronounced...
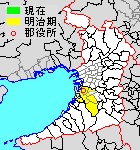
令制国一覧 > 畿内 > 和泉国 > 大鳥郡 日本 > 近畿地方 > 大阪府 > 大鳥郡 大阪府大鳥郡の範囲 大鳥郡(おおとりぐん)は、かつて和泉国・堺県・大阪府にあった郡。 郡域 1880年(明治13年)に行政区画として発足した当時の郡域は、現在の行政区画では概ね以下の区域に相当する。 堺市堺区(埋立地および郡区町村編制法における堺区�...

B92 Edificio de B92 en Novi BeogradTipo de canal GeneralistaPropietario Astonko doo 84.99%,B92 Trust 11,35%,otros 3,66%País Serbia SerbiaFundación 1989Fundador Veran Matić, Dragan Đilas.Inicio de transmisiones 1989 (radio)2000 (televisión)Personas clave Veran Matić, Manja GrčićÁrea de transmisión SerbiaUbicación BelgradoSitio web www.b92.net[editar datos en Wikidata] B92 (en cirílico serbio Б92) es un canal de radio y televisión con cobertura nacional con sede en ...

諾加萊斯(西班牙語:Heroica Nogales),是墨西哥的城市,由索諾拉州負責管轄,位於該國北部的美墨邊界上,與美國的諾加利斯相鄰,兩者的鎮名具有相同的字母拼法。始建於1884年,面積1,675平方公里,海拔高度1,199米,每年平均降雨量523毫米,2010年人口212,533。 外部連結 Link to tables of population data from Census of 2005 INEGI: Instituto Nacional de Estadística, Geografía e Informática Nogales, Ayun...