משלים ל-2
|
Read other articles:

Guiguzi Hanzi: 鬼谷子 Alih aksara Mandarin - Hanyu Pinyin: Guǐgǔzi - Wade-Giles: Kuei3 Ku3 Tzu Wang Xu Hanzi tradisional: 王詡 Hanzi sederhana: 王诩 Alih aksara Mandarin - Hanyu Pinyin: Wáng Xǔ - Wade-Giles: Wang2 Hsü3 Guiguzi Guiguzi (鬼谷子) adalah judul yang diberikan kepada sejumlah tulisan yang dikumpulkan para Periode Negara Berperang. Karya yang terdiri dari 6.000 hingga 7.000 karakter Tionghoa dan berisi tentang metode lobi politik berdasarkan pemikiran Taoisme. Terdap...

Artikel ini tidak memiliki bagian pembuka yang sesuai dengan standar Wikipedia. Mohon tulis paragraf pembuka yang informatif sehingga pembaca dapat memahami maksud dari Daftar penulis Mesir. Contoh paragraf pembuka Daftar penulis Mesir adalah .... (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Naguib Mahfouz Mustafa Mahmoud Ahmed Shawki (1868–1932) Hafez Ibrahim (1872–1932) Mustafa Lutfi al-Manfaluti (1876-1920) Salama Moussa (1887–1958) Edwar al-Kharrat (1926-2015)...

Job 30← chapter 29chapter 31 →The whole Book of Job in the Leningrad Codex (1008 C.E.) from an old fascimile edition.BookBook of JobHebrew Bible partKetuvimOrder in the Hebrew part3CategorySifrei EmetChristian Bible partOld TestamentOrder in the Christian part18 Job 30 is the 30th chapter of the Book of Job in the Hebrew Bible or the Old Testament of the Christian Bible.[1][2] The book is anonymous; most scholars believe it was written around 6th century BCE.[...

Pour les articles homonymes, voir Acteur (homonymie) et Comédien (homonymie). Acteurs en costume d'époque, plaisantant en attendant les prises de vue d'un téléfilm à l'hôtel Somerset à Londres. Actrice jouant au théâtre du Kaléidoscope, à Cracovie en mai 2018). Un acteur ou une actrice (ou comédien et comédienne), prête son physique ou sa voix à un personnage fictif au théâtre, au cinéma, à la télévision, à la radio, ou encore dans un jeu vidéo, selon des règles artis...

Artikel ini bukan mengenai Franz Strauss. Franz Josef StraussStrauss sebagai Menteri Keuangan Menteri President BayernMasa jabatan6 November 1978 – 3 Oktober 1988 PendahuluAlfons GoppelPenggantiMax StreiblMenteri Keuangan FederalMasa jabatan2 Desember 1966 – 22 Oktober 1969 PendahuluKurt SchmückerPenggantiAlex MöllerMenteri Pertahanan FederalMasa jabatan16 Oktober 1956 – 16 Desember 1962 PendahuluTheodor BlankPenggantiKai-Uwe von HasselMenteri Urusan Atom Fe...

Kesultanan BolangoPohala'a Bolango1482–1862Lambang Kesultanan Bolango yang terukir pada makam Sultan Ibrahim Duawulu bergelar Ti Hubulo atau disebut Raja GobelIbu kotaTapaBahasa yang umum digunakanBahasa BolangoAgama Sunni IslamPemerintahanMonarki KonstitusionalRaja/Sultan • 1482 - 1535 Raja Datau• 1752 - 1772 Raja Ibrahim Duawulu atau Ti Hubulo bergelar Ti Aulia Salihin• 1857-1862 Raja Tilahunga atau Abdullatif bin Muhammad Saleh Tilahunga Wadipalapa Sejarah&...

9th episode of the 6th season of Better Call Saul Fun and GamesBetter Call Saul episodePromotional posterEpisode no.Season 6Episode 9Directed byMichael MorrisWritten byAnn CherkisProduced by Jenn Carroll Bob Odenkirk James Powers Featured music Perfect Dayby Dresage and Slow Shiver Any Way You Want Itby Journey Cinematography byMarshall AdamsEditing bySkip MacdonaldOriginal air dateJuly 18, 2022 (2022-07-18)Running time56 minutesGuest appearances Ed Begley Jr. as Clifford...

Afrika Timur ItaliaAfrica Orientale Italiana1936–1960 Bendera Lambang Semboyan: Foedere et Religione TenemurLagu kebangsaan: Marcia Reale d'Ordinanza Afrika Timur Italia pada tahun 1936. <div legend> Italian East Africa Dikuasai pada 1940 Derah pendudukan Italia Kerajaan Italia> StatusKoloni ItaliaIbu kotaAddis AbabaBahasa yang umum digunakanItalia, Amhar, SomaliKaisar • 1936–1960 Victor Emmanuel III Viceroy&#...

Anggrek hitam Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Monokotil Ordo: Asparagales Famili: Orchidaceae Subfamili: Epidendroideae Genus: Coelogyne Spesies: C. pandurata Nama binomial Coelogyne pandurata Anggrek hitam (Coelogyne pandurata) adalah spesies anggrek yang tumbuh di Semenanjung Malaya, Kalimantan, dan Sumatra.[1][2] Angrek hitam adalah maskot flora Provinsi Kalimantan Timur. Saat ini, habitat asli anggrek hitam mengalami ...
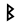
此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

Данио-рерио Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые рыбыИн�...

Penghargaan Filmfare ke-1Tanggal21 Maret 1954 [1]TempatMetro Cinema, BombayPembawa acaraDavid Abraham CheulkarSorotanFilm TerbaikDo Bigha ZaminPenghargaan terbanyakBaiju Bawra (2) Penghargaan Filmfare ke-2 → Penghargaan Filmfare ke-1 diadakan pada 21 Maret 1954, untuk menghormati Sinema Hindi terbaik pada tahun 1953. Tahun itu mereka dikenal sebagai Clare Awards, setelah Clare Mendonca, kritikus film The Times of India yang meninggal pada tahun yang sama.[1] Pengha...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مايو 2023) جغرافيا كينيامعلومات عامةالبلد كينيا القارة إفريقيا الحدود إثيوبياالصومالتنز�...

Paper-based recording medium Overpunch redirects here. For the COBOL code, see Signed overpunch. This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (December 2023) A 12-row/80-column IBM punched card from the mid-twentieth century A punched card (also punch card[1] or punched-card[2]) is a piece of card stock that stores digital data u...

Design pattern in computer programming This article may contain excessive or irrelevant examples. Please help improve the article by adding descriptive text and removing less pertinent examples. (January 2011) In software engineering, the adapter pattern is a software design pattern (also known as wrapper, an alternative naming shared with the decorator pattern) that allows the interface of an existing class to be used as another interface.[1] It is often used to make existing classes...

Poverty on Native American reservations Allen, South Dakota, on the Pine Ridge Reservation, has the lowest per capita income in the country. The alcohol depo of Whiteclay, Nebraska sold over 4.9 million 12-ounce cans of beer in 2010 almost exclusively to Oglala Lakota from the reservation.[1] Part of a series onNative Americans in the United States History Paleo-Indians Lithic stage Archaic period in the Americas Formative stage Classic stage Post-Classic stage Woodland period Age of ...

Pietà di MichelangeloAutoreMichelangelo Buonarroti Data1497-1499 MaterialeMarmo bianco di Carrara Dimensioni174×195×69 cm UbicazioneBasilica di San Pietro in Vaticano, Città del Vaticano Coordinate41°54′08″N 12°27′12″E41°54′08″N, 12°27′12″E Modello 3D La Pietà di Michelangelo è una scultura fatta in marmo realizzata da Michelangelo Buonarroti e conservata nella basilica di San Pietro in Vaticano. Databile tra il 1497 e il 1499, la Pietà è considerata il primo ...

Part of a series on theNation of Islam Influencers Satokata Takahashi Noble Drew Ali Leaders Wallace Fard Muhammad Elijah Muhammad Malcolm X Warith Deen Mohammed Louis Farrakhan Tynnetta Muhammad Ishmael Muhammad Ava Muhammad David Muhammad James 3X Khalid Muhammad Beliefs and theology Saviours' Day Nation of Islam and antisemitism Tribe of Shabazz Yakub History Million Man March Millions More Movement Justice or Else Publications A Torchlight for America The Final Call Muhammad Speaks How to...

Cet article est une ébauche concernant le sport. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations du projet sport. Le knattleikr est un ancien sport de balle joué par les vikings en Islande. Les règles exactes sont aujourd'hui peu connues mais quelques éléments permettent d'en voir les apparences[1]. Il s'agissait d'un sport collectif où s'affrontaient deux équipes, chacune dotée d'un capitaine. Chaque joueur était muni d'un bâton...

Japanese samurai Kagawa ChikakazuTomb of Kagawa Chikakazu near the Okō CastleNative name香川 親和Born1567Tosa ProvinceDied1587(1587-00-00) (aged 19–20)Okō Castle, Tosa ProvinceAllegianceChōsokabe clanUnitKagawa clanCommandsAmagiri CastleBattles/warsInvasion of Shikoku (1585)RelationsChōsokabe Motochika (father)Kagawa Yukikage (adopted father) In this Japanese name, the surname is Kagawa. Kagawa Chikakazu (香川親和, 1567 – 1587) also known as Chōsokabe Chikakazu was a Jap...






