![]() ОћОЊОњОъОћ ОЕОю ОћОцОеОЊОЋОДОА ОЕОю ОљОЋОюОЉОеОА
ОћОЊОњОъОћ ОЕОю ОћОцОеОЊОЋОДОА ОЕОю ОљОЋОюОЉОеОА
ОћОцОеОЊОЋОДОА ОЕОю ОљОЋОюОЉОеОА ОћОЋОљ ОћОўОЎОбОЋОЪ ОЏОЎ ОљОцОюОф ОЕОъОЎ ОћОюОЎОюОћ ОАОЋОфОеОф ОљОф ОћОћОаОЌОћ ОЕОю ОЎОДОЋОЮ ОАОўОўОЎ ОљОЎОаОАОЋОцОЎ ОЋОаОдОЌОЎ. ОћОЋОљ ОфОЋОљОе ОбОю ОЎОЊОЎ ОћОљОАОўОеОЋОаОЋОЮ ОћОњОеОъОаОЎ ОћОЎОЎОаОеОЎОџ ОЋОЎОюОћОюОЮ ОљОЋОюОЉОеОА ОЉОЕОаОф 1823 (ОљОџ ОцОЋОеОАОЮ ОеОД ОЉ-1826 ОбОю ОЎОЊОЎ ОЎОЋОћОљОЪ ОљОюОеОў ОЉОЋОЊОћ) ОЋОљОБ ОюОцОаОЎ ОЏОЪ ОбОю ОЎОЊОЎ ОЎОЋОћОљОаОА ОДОцОюОе ОЉ-1610 ОЋОљОЊОъОЋОаОЊ ОћОЎОЎОюОЎ ОЋОќ'ОљОЪ ОцОЎОюОЎОц ОЊОћ ОЕОАОЋ ОЉОъОљОћ Оћ-18. ОќОЋОћОЎ ОљОЌОф ОћОеОљОЎОЋОф ОюОЎОДОЋОЮ ОюОљ ОАОўОўОЎ ОћОъОфОЋОљОе ОЉОљОъОдОбОЋОф ОфОљОЋОеОЎОЎОф "ОћОъОцОЦ ОћОњОЊОЋОю". Оћ"ОцОеОЊОЋОДОА" ОЎОЊОЋОб ОњОЮ ОЉОЕОЮ "ОцОеОЊОЋОДОА ОЕОъОЎ ОћОюОЎОюОћ ОћОљОцОюОЎОЮ".
ОћОаОЌОЋОф
 ОъОћ ОљОЮ ОЏОю ОДОЋ ОеОљОЎОЎОћ ОћОЎОћ ОаОњОъОе ОЉОЏОЋОЏОЉ? (ОћОаОЌОф ОћОЎОДОЋОЮ ОћОљОЎОаОАОЋОцОЎ ОъОА' 2)
ОъОћ ОљОЮ ОЏОю ОДОЋ ОеОљОЎОЎОћ ОћОЎОћ ОаОњОъОе ОЉОЏОЋОЏОЉ? (ОћОаОЌОф ОћОЎОДОЋОЮ ОћОљОЎОаОАОЋОцОЎ ОъОА' 2)
ОљОЮ ОаОаОЎОЌ ОЏОЎ ОЉОЎОДОЋОЮ ОЎОЕ ОъОАОцОе ОљОЎОаОАОЋОцОЎ ОЕОю ОЏОЋОЏОЉОЎОЮ ОъОљОЎОеОЎОЮ ОћОъОцОЋОќОеОЎОЮ ОЉОљОЋОцОЪ ОљОЌОЎОЊ, ОљОќОЎ:
- ОАОџ ОћОЉОћОЎОеОЋОф ОћОаОеОљОЎОф ОћОъОфОДОЉОюОф ОъОъОбОеОЏОф ОЕОю ОЏОЋОЏОЉОЎОЮ ОЉОъОеОЌОД ОаОфОЋОЪ ОљОЎОаОћ ОфОюОЋОЎОћ ОЉОъОеОЌОД ОќОћ;
- ОЏОю ОДОЋ ОеОљОЎОЎОћ ОдОеОЎОџ ОюОћОЎОњОъОе ОЉОАОЋОцОЋ ОЕОю ОЊОЉОе ОЉОцОаОЎ ОћОЕОўОЌ ОЕОю ОЏОЋОЏОЉ;
- ОЏОю ОаОДОЋОЊОћ ОЉОЕОъОЎОЮ ОдОеОЎОЏОћ ОюОћОЎОЋОф ОЉОћОЎОеОћ ОЏОъОЋ ОцОаОЎОЋ ОЕОю ОЏОЋОЏОЉ.
ОћОфОЉОЋОаОаОЋОф ОЉОљОЋОцОД ОъОфОЋОџ ОЎОбОе ОбОЉОЋОф ОЋОъОЎОЕОЋОеОЎ ОбОЕОЋОЎОћ ОюОћОЊОњОЎОЮ ОљОцОДОў ОќОћ: ОЏОю ОДОЋ ОеОљОЎОЎОћ ОЎОАОфОЎОЎОЮ ОЉОбОЦ, ОЋОюОЏОЪ ОћОљОЋОцОД ОЎОЋОАОфОе ОЏОЋОюОЋ ОбОю ОЎОЊОЎ ОбОдОЎ ОћОЎОбОе.
ОъОћОЎОеОЋОф ОћОљОЋОе ОћОЎОљ ОАОЋОцОЎОф, ОЋОюОЏОЪ ОЏОЏОю ОЕОљОЊОЮ ОЎОфОЉОЋОаОЪ ОеОЌОЋОД ОЎОЋОфОе, ОЏОџ ОћОЋОљ ОЎОеОљОћ ОЏОЋОЏОЉОЎОЮ ОбОфОЎОДОЎОЮ ОЎОЋОфОе. ОбОю ОъОаОф ОЕОћОЏОЋОЏОЉОЎОЮ ОЎОЎОеОљОЋ ОъОцОЋОќОеОЎОЮ ОЉОљОЋОцОЪ ОљОЌОЎОЊ ОЉОЌОюОю, ОљОЋОеОЮ ОдОеОЎОџ ОюОћОЎОцОюОў ОъОъОДОЋОъОЋОф ОЉОћОЮ ОдОцОЎОцОЋОф ОћОЏОЋОЏОЉОЎОЮ ОћОЎОЎОфОћ ОќОћОћ, ОЉОбОф ОЕОаОцОюОў ОћОљОЋОе, ОюОдОцОЎОцОЋОф ОћОЏОЋОЏОЉОЎОЮ ОЉОАОЉОЎОЉОф ОћОдОЋОцОћ. ОћОАОЉОе ОцОЕОЋОў ОюОцОеОЊОЋОДОА ОЕОю ОљОЋОюОЉОеОА ОъОаОЎОЌ ОЏОЎ ОюОљ ОћОЎОЋ ОЕОЎОаОЋОЎОЎОЮ ОЊОеОъОўОЎОЎОЮ ОЉОцОЎОќОЋОе ОћОЏОЋОЏОЉОЎОЮ ОЉОъОЕОџ ОћОќОъОЪ ОћОќОћ. ОъОЏОљОЪ ОаОЋОЉОб ОЏОЎ ОљОЮ ОћОЎОДОЋОЮ ОћОЎОћ ОљОЎОаОАОЋОцОЎ ОЉОќОъОЪ ОЋОЉОъОеОЌОЉ, ОЕОўОБ ОћОљОЋОе ОћОъОфОДОЉОю ОъОћОЏОЋОЏОЉОЎОЮ ОћОЎОћ ОљОЎОаОАОЋОцОЎ.
ОДОцОюОе ОеОљОћ ОљОф ОћОцОеОЊОЋОДОА ОЏОфОЋОъОџ ОЉОЎОДОЋОЮ ОаОеОљОћ ОАОЋОцОЎ, ОљОЋ ОюОцОЌОЋОф ОЉОбОю ОъОАОцОе ОАОЋОцОЎ ОЕОю ОЏОЋОЏОЉОЎОЮ. ОюОцОЎ ОфОЋОеОф ОћОЎОЌОАОЋОф ОћОЏОюОюОЎОф, ОћОцОеОЊОЋОДОА ОЎОЏОЋОю ОюОћОЋОцОЎОб ОљОцОЎОюОЋ ОЉОЎОДОЋОЮ ОАОЋОцОЎ[1]: ОюОъОеОЋОф ОЕОћОЕОъОЎОЮ ОюОљ ОЎОћОЎОЋ ОЉОћОЎОеОЎОЮ ОЉОъОЎОЊОћ ОљОЎОаОАОЋОцОЎОф, ОЏОю ОаОДОЋОЊОћ ОЉОћОЮ ОфОћОЎОћ ОЉОћОЎОеОћ ОЏОцОаОЎОЋ ОЕОю ОЏОЋОЏОЉ.
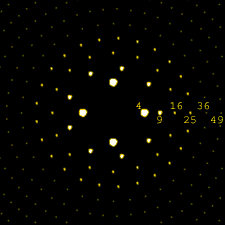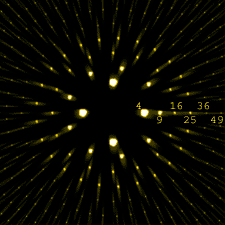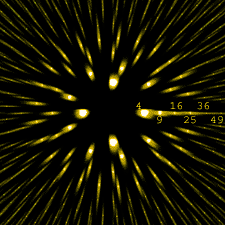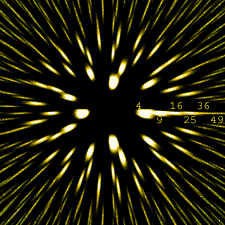 ОЉОЎОДОЋОЮ ОЉОбОю ОЕОюОЋОЕОћ ОъОъОЊОЎОЮ ОбОЮ ОцОЎОќОЋОе ОљОЌОЎОЊ ОЕОю ОЏОЋОЏОЉОЎОЮ, ОъОАОцОе ОћОЏОЋОЏОЉОЎОЮ ОЎОћОЎОћ ОЎОЌОАОЎ ОюОаОцОЌ. ОљОЮ ОаОфОЉОЋОаОЪ ОЉОЕОўОЌ ОћОцОаОЎОЮ ОЕОю ОДОюОЎОцОЋОф ОЏОЊОЋОеОЎОЋОф ОЉОбОюОЋОф ОъОеОЏОќ ОъОЕОЋОфОБ, ОаОеОљОћ ОЏОЎ ОъОАОцОе ОћОЏОЋОЏОЉОЎОЮ ОЉОЏОю ОДОюОЎОцОћ ОЎОћОЎОћ ОЎОЌОАОЎ ОюОеОЎОЉОЋОб ОеОЊОЎОЋОА ОћОДОюОЎОцОћ. ОЉОфОъОЋОаОћ ОюОбОЎОю, ОдОЋОъОдОъОЋ ОћОДОюОЎОцОЋОф ОюОўОЉОбОЋОф ОЊОЋ-ОъОъОЊОЎОЋОф ОюОдОЋОеОџ ОћОъОЌОЕОћ.
ОЉОЎОДОЋОЮ ОЉОбОю ОЕОюОЋОЕОћ ОъОъОЊОЎОЮ ОбОЮ ОцОЎОќОЋОе ОљОЌОЎОЊ ОЕОю ОЏОЋОЏОЉОЎОЮ, ОъОАОцОе ОћОЏОЋОЏОЉОЎОЮ ОЎОћОЎОћ ОЎОЌОАОЎ ОюОаОцОЌ. ОљОЮ ОаОфОЉОЋОаОЪ ОЉОЕОўОЌ ОћОцОаОЎОЮ ОЕОю ОДОюОЎОцОЋОф ОЏОЊОЋОеОЎОЋОф ОЉОбОюОЋОф ОъОеОЏОќ ОъОЕОЋОфОБ, ОаОеОљОћ ОЏОЎ ОъОАОцОе ОћОЏОЋОЏОЉОЎОЮ ОЉОЏОю ОДОюОЎОцОћ ОЎОћОЎОћ ОЎОЌОАОЎ ОюОеОЎОЉОЋОб ОеОЊОЎОЋОА ОћОДОюОЎОцОћ. ОЉОфОъОЋОаОћ ОюОбОЎОю, ОдОЋОъОдОъОЋ ОћОДОюОЎОцОЋОф ОюОўОЉОбОЋОф ОЊОЋ-ОъОъОЊОЎОЋОф ОюОдОЋОеОџ ОћОъОЌОЕОћ.
ОЊОеОџ ОъОЊОЋОЎОДОф ОЎОЋОфОе ОюОћОфОЉОЋОаОЪ ОЉОцОеОЊОЋОДОА ОћОЎОљ ОюОћОдОЎОЉ ОљОф ОћОљОеОЦ ОЉОъОеОЏОќ ОЏОЊОЋОеОЎОЮ ОЉОбОюОЎ ОеОЊОЎОЋОАОЎОЮ ОЕОЋОаОЎОЮ. ОљОЮ ОћОЎОДОЋОЮ ОћОЋОъОЋОњОаОЎ ОЋОљОЎОаОАОЋОцОЎ, ОљОќ ОЊОеОџ ОДОюОЎОцОћ ОЏОЊОЋОеОЎОф ОЉОеОЊОЎОЋОА r ОАОЉОЎОЉ ОЏОЊОЋОе ОћОљОеОЦ ОЎОбОЉОЋОе ОЕОўОБ ОъОАОЋОЎОЮ ОЕОю ОљОЋОе ОъОћОЏОЋОЏОЉОЎОЮ. ОбОю ОЏОЊОЋОе ОЉОеОЊОЎОЋОА r+x, ОъОАОцОе ОћОЏОЋОЏОЉОЎОЮ ОњОЊОю ОюОцОЎ ОеОЎОЉОЋОб ОћОъОеОЌОД, ОљОџ ОћОЕОўОБ ОъОЏОю ОЏОЋОЏОЉ ОДОўОЪ ОюОцОЎ ОеОЎОЉОЋОб ОћОъОеОЌОД. ОъОЏОљОЪ, ОюОЕОфОЎ ОћОДОюОЎОцОЋОф (ОЉОеОЊОЎОЋОА r ОЋОЉОеОЊОЎОЋОА r+x) ОЕОўОБ ОќОћОћ, ОЋОюОЏОЪ ОћОЉОћОЎОеОЋОф ОЕОюОћОЪ ОфОћОЎОћ ОќОћОћ ОљОБ ОћОЎОљ. ОљОЮ ОћОЎОДОЋОЮ ОћОЎОћ ОљОЎОаОАОЋОцОЎ (ОЉОњОЎОю ОЋОЉОаОцОЌ) ОЋОЉОбОю ОцОЎОќОЋОе ОЕОЋОЋОћ ОЕОю ОћОЏОЋОЏОЉОЎОЮ, ОљОќ ОЎОћОЎОЋ ОљОЎОаОАОЋОБ ОДОюОЎОцОЋОф ОЏОљОюОћ ОЋОюОљОЋОе ОъОЏОю ОДОюОЎОцОћ ОЎОћОЎОћ ОъОАОцОЎОД ОќОъОЪ ОюОћОњОЎОб ОюОЏОЊОЋОе ОћОљОеОЦ - ОЏОюОЋОъОе, ОЕОъОЎ ОћОљОеОЦ ОЎОћОЎОЋ ОЉОћОЎОеОЎОЮ ОфОъОЎОЊ.
ОћОћОАОЉОе ОћОъОДОЋОЉОю
ОћОћОАОЉОе ОћОъОДОЋОЉОю ОюОцОеОЊОЋОДОА ОЕОю ОљОЋОюОЉОеОА ОЊОЋОеОЕ ОЎОДОЋОЮ ОъОфОеОЌОЉ ОљОЕОе ОњОЎОюОЋ ОАОЋОцОЎ.
ОъОћОЎОеОЋОф ОћОљОЋОе ОћОЎОљ ОАОЋОцОЎОф
ОЏОЏОю ОЕОЏОЋОЏОЉ ОаОъОдОљ ОеОЌОЋОД ОЎОЋОфОе ОъОдОЋОцОћ ОбОю ОЏОЊОЋОе ОћОљОеОЦ, ОЏОџ ОЎОЎОДОЌ ОЎОЋОфОе ОќОъОЪ ОюОљОЋОе ОъОћОЏОЋОЏОЉ ОюОћОњОЎОб ОљОюОЎОЋ. ОъОАОЎОЉОћ ОќОЋ, ОЏОЏОю ОЕОъОЉОЎОўОЎОЮ ОеОЌОЋОД ОЎОЋОфОе ОљОю ОфОЋОџ ОћОЎОДОЋОЮ - ОъОЉОЎОўОЎОЮ ОюОъОбОЕОћ ОъОЋОДОЊОЮ ОЎОЋОфОе ОљОю ОћОбОЉОе. ОбОЋОЉОЊОћ ОќОЋ ОъОћОЋОЋОћ ОъОеОЏОЎОЉ ОбОЎОДОеОЎ ОЉОћОАОЉОе ОћОъОДОЋОЉОю ОюОцОеОЊОЋОДОА ОЕОю ОљОЋОюОЉОеОА, ОљОЮ ОЏОЎ ОћОЎОљ ОљОЎОаОћ ОЎОЏОЋОюОћ ОюОћОАОЉОЎОе ОљОф ОћОцОеОЊОЋОДОА ОЏОЕОюОбОдОъОћ - ОюОъОћОЎОеОЋОф ОћОљОЋОе ОљОЎОЪ ОДОЕОе ОЎОЕОЎОе ОюОдОцОЎОцОЋОф ОћОљОаОеОњОЎОћ ОЋОюОЏОъОЋОф ОћОљОЋОе ОћОъОњОЎОбОћ ОюОаОДОЋОЊОћ ОъОАОЋОЎОъОф.
ОњОЎОюОЋ ОћОАОЋОцОЎ ОЕОю ОћОЎОДОЋОЮ; ОЏОю ОъОДОЋОеОЋОф ОћОљОЋОе ОћОЮ ОЉОъОеОЌОД ОАОЋОцОЎ
ОљОЊОњОе ОљОюОЪ ОцОЋ ОћОЎОћ ОћОеОљОЕОЋОЪ ОљОЕОе ОцОфОе ОљОф ОћОцОеОЊОЋОДОА ОЕОю ОљОЋОюОЉОеОА, ОЏОљОЕОе ОЏОфОЉ ОЉОъОљОъОе Eureka: A Prose Poem ОЉ-1848:
- "ОюОЋ ОћОЎОћ ОеОдОБ ОћОЏОЋОЏОЉОЎОЮ ОљОЎОаОАОЋОцОЎ, ОљОќ ОеОДОб ОћОЕОъОЎОЮ ОћОЎОћ ОъОдОЎОњ ОЉОцОаОЎОаОЋ ОЉОћОЎОеОЋОф ОљОЌОЎОЊОћ, ОъОЕОЋОЮ ОЕОюОљ ОЎОЏОЋОюОћ ОюОћОЎОЋОф ОаОДОЋОЊОћ ОЉОЕОъОЎОЮ ОЉОћ ОюОљ ОЎОћОЎОћ ОЏОЋОЏОЉ. ОћОъОдОЉ ОћОЎОЌОЎОЊ, ОљОЮ ОЏОЪ, ОЉОЋ ОаОЋОЏОю ОюОћОЉОЎОЪ ОфОЌОф ОфОаОљОЎОЮ ОљОюОЋ ОљОф ОћОЌОюОюОЎОЮ ОћОеОЎОДОЎОЮ ОљОЕОе ОћОўОюОАОДОЋОцОЎОЮ ОЕОюОаОЋ ОъОЋОдОљОЎОЮ ОЉОЏОю ОћОЏОЎОЋОЋОаОЎОЮ, ОЎОћОЎОћ ОљОЮ ОаОаОЎОЌ ОЏОЎ ОћОъОеОЌОД ОЕОю ОљОЋОфОЋ ОеОДОб ОљОЌОЎОЊ ОћОЋОљ ОЏОћ ОеОЌОЋОД, ОЕОљОБ ОДОеОЪ ОљОЋОе ОъОъОаОЋ ОбОЊОЎОЎОЪ ОюОљ ОћОАОцОЎОДОћ ОюОћОњОЎОб ОљОюОЎОаОЋ."[2]
ОюОцОЎ ОћОфОљОЋОеОЎОћ ОћОъОДОЋОЉОюОф (ОфОљОЋОеОЎОЎОф ОћОъОцОЦ ОћОњОЊОЋОю), ОњОЎОю ОћОЎОДОЋОЮ ОћОЋОљ ОАОЋОцОЎ, ОЋОћОЏОЋОЏОЉОЎОЮ ОаОЋОдОеОЋ ОюОцОаОЎ ОќОъОЪ ОАОЋОцОЎ. ОюОЏОЪ, ОЏОцОЎ ОЕОћОдОЎОб ОцОЋ, ОЏОЊОЋОе ОћОљОеОЦ ОљОЎОаОЋ ОъОДОЉОю ОљОЋОе ОЏОЋОЏОЉОЎОЮ ОъОбОЉОе ОюОъОеОЌОД ОъОАОЋОЎОЮ. ОюОцОЎ ОфОљОЋОеОЎОћ ОќОЋ, ОћОЕОъОЎОЮ ОћОЎОЋ ОЉОћОЎОеОЎОЮ ОћОеОЉОћ ОЎОЋОфОе ОЉОбОЉОе, ОЉОъОЎОЋОЌОЊ ОЉОбОЎОЊОЪ ОћОеОДОЋОъОЉОЎОаОдОЎОћ ОЕОю ОћОЎОДОЋОЮ ОћОдОбОЎОе, 378,000 ОЕОаОћ ОљОЌОеОЎ ОћОъОцОЦ ОћОњОЊОЋОю. ОЏОю ОћОаОДОЋОЊОЋОф ОЉ"ОЕОъОЎОЮ" ОЉОќОъОЪ ОћОќОћ ОћОЎОЋ ОЉОћОЎОеОЋОф ОЎОЋОфОе ОъОћОЕОъОЕ, ОюОъОеОЋОф ОћОъОеОЌОД ОћОДОдОе ОЎОЌОАОЎОф ОЕОћОљОЋОе ОћОЎОћ ОъОАОЋОњОю ОюОбОЉОЋОе; ОЊОЉОе ОќОћ ОъОеОъОќ ОЏОЎ ОеОЋОЉ ОДОеОаОЎ ОћОљОЋОе ОЕОъОњОЎОбОЋОф ОљОюОЎОаОЋ ОъОДОЋОеОЪ ОюОљ ОЉОЏОЋОЏОЉ, ОљОюОљ ОЉ"ОЕОљОеОЎОЋОф" ОЕОю ОћОъОцОЦ ОћОњОЊОЋОю.
ОћОъОеОЌОЉ ОъОфОцОЕОў
ОЉОбОЋОЊ ОћОъОеОЌОД ОћОАОЋОцОЎ ОюОъОДОЋОеОЪ ОЕОю ОДОеОаОЎ ОћОљОЋОе ОюОљ ОцОЋОфОе ОљОф ОћОцОеОЊОЋОДОА ОЏОЕОюОбОдОъОЋ, ОфОљОЋОеОЎОЎОф ОћОъОцОЦ ОћОњОЊОЋОю ОЏОЋОюОюОф ОњОЮ ОћОфОцОЕОўОЋОф ОЕОю ОћОъОеОЌОЉ ОбОдОъОЋ (ОЋОюОљ ОеОД ОћОъОеОЌОД ОЉОЎОЪ ОбОдОъОЎОЮ ОЉОъОеОЌОЉ), ОљОЕОе ОЎОЏОЋОюОћ ОюОњОеОЋОЮ ОюОљОаОеОњОЎОћ ОЕОю ОћОљОЋОе ОћОаОцОюОў ОюОДОўОЋОЪ ОЉОљОъОдОбОЋОф ОћОАОЌОћ ОюОљОЊОЋОЮ. ОћОфОцОЕОўОЋОф ОћОъОеОЌОЉ ОњОеОъОћ ОюОеОъОЋОф ОћОДОеОЎОаОћ ОћОњОЉОЋОћОЋОф ОъОћОъОцОЦ ОћОњОЊОЋОю ОюОћОЎОЋОф ОъОЋОАОЌОЋОф ОюОљОЊОЋОЮ ОбОЊ ОюОњОюОЎ ОъОЎОДОеОЋ; ОљОаОЋ ОъОќОћОЎОЮ ОДОеОЎОаОћ ОќОЋ ОбОЮ ОДОеОЎОаОф ОћОеОДОб ОћОДОЋОАОъОЎОф. ОќОћ ОъОАОЉОЎОе ОљОф ОдОцОЎОцОЋОф ОћОљОЋОе ОћОаОъОЋОЏОћ ОЎОЌОАОЎОф ОЉОЕОъОЎОЮ ОЕОюОаОЋ, ОюОъОеОЋОф ОћОЉОћОЎОеОЋОф ОћОбОдОЋОъОћ ОћОъОЕОЋОбОеОф ОЕОю ОћОъОцОЦ ОћОњОЊОЋОю. ОћОћОАОЌОћ ОюОљОЊОЋОЮ ОъОЕОцОЎОбОћ ОњОЮ ОбОю ОљОЋОе ОъОЏОЋОЏОЉОЎОЮ ОеОЌОЋОДОЎОЮ ОЋОДОЋОЋОќОеОЎОЮ, ОљОџ ОћОЕОцОбОћ ОќОЋ ОъОцОЌОЎОфОћ ОљОф ОћОљОЋОе ОЉОАОЊОе ОњОЋОЊОю ОљОЌОЊ ОЉОюОЉОЊ.
ОеОљОЋ ОњОЮ
ОДОЎОЕОЋОеОЎОЮ ОЌОЎОдОЋОаОЎОЎОЮ
ОћОбОеОЋОф ОЕОЋОюОЎОЎОЮ