![]() ОљОеОЉОбОћ ОљОЋОеОЉОЎОўОюОЎ sp3.
ОљОеОЉОбОћ ОљОЋОеОЉОЎОўОюОЎ sp3.
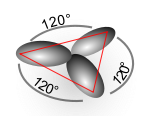 ОЕОюОЋОЕОћ ОљОЋОеОЉОЎОўОюОЎ sp2.
ОЕОюОЋОЕОћ ОљОЋОеОЉОЎОўОюОЎ sp2.
ОЉОЏОЎОъОЎОћ ОДОЋОЋОаОўОЎОф ОЋОЉОъОЏОаОЎОДОф ОћОДОЋОЋОаОўОЎОЮ, ОћОЏОюОљОф ОљОЋОеОЉОЎОўОюОЎОЮ ОљОўОЋОъОЎОЎОЮ (ОъОЏОЋОаОћ ОњОЮ ОћОЎОЉОеОЎОЊОЎОќОдОЎОЎОф ОљОЋОеОЉОЎОўОюОЎОЮ) ОћОЎОљ ОбОеОЉОЋОЉ ОЕОю ОћОљОЋОеОЉОЎОўОюОЎОЮ ОЕОю ОљОўОЋОъОЎОЮ ОћОЎОЋОдОеОЎОЮ ОДОЕОе ОЏОЎОъОЎ, ОЏОюОЋОъОе ОъОЋОюОДОЋОюОћ, ОќОћ ОбОЮ ОќОћ.
ОћОљОЋОеОЉОЎОўОюОЎОЮ, ОЕОћОЮ ОъОАОюОЋОюОЎ ОћОљОюОДОўОеОЋОаОЎОЮ ОЉОъОеОЌОЉ, ОъОфОбОеОЉОЉОЎОЮ, ОљОЋ ОъОЏОюОЎОљОЎОЮ ОћОљОЌОЊ ОљОф ОћОЕОаОЎ, ОЏОЊОЎ ОюОЎОдОЋОе ОљОЋОеОЉОЎОўОюОЎОЮ ОЌОЊОЕОЎОЮ ОЕОъОфОљОЎОъОЎОЮ ОюОъОЋОюОДОЋОюОћ ОЉОъОДОЋОЮ ОћОљОЋОеОЉОЎОўОюОЎОЮ ОћОаОцОеОЊОЎОЮ ОЕОъОфОљОЎОъОЎОЮ ОюОљОўОЋОъОЎОЮ ОЉОЋОЊОЊОЎОЮ.
ОЉОаОЎОАОЋОЌ ОцОЎОќОЎОДОюОЎ ОЕОю ОъОЏОаОЎОДОф ОћОДОЋОЋОаОўОЎОЮ, ОћОљОЋОеОЉОЎОўОюОЎОЮ ОћОъОЋОЏОюОљОЎОЮ ОћОЮ ОћОъОдОЉОЎОЮ ОћОбОдОъОЎОЎОЮ ОЕОю ОћОъОЋОюОДОЋОюОћ, ОЉОъОДОЋОЮ ОћОљОЋОеОЉОЎОўОюОЎОЮ ОћОаОцОеОЊОЎОЮ ОЕОћОЮ ОћОъОдОЉОЎОЮ ОћОбОдОъОЎОЎОЮ ОЕОю ОћОљОўОЋОъОЎОЮ.
ОљОЋОеОЉОЎОўОю ОЉОЏОюОю, ОЋОљОЋОеОЉОЎОўОю ОљОўОЋОъОЎ ОЉОцОеОў, ОъОЎОЎОдОњ ОљОф ОћОћОАОфОЉОеОЋОф ОЕОю ОћОљОюОДОўОеОЋОЪ ОюОћОЎОъОдОљ ОЉОаОцОЌ ОъОАОЋОЎОЮ ОбОю ОцОаОЎ ОќОъОЪ ОъОАОЋОЎОЮ. ОюОЏОЪ ОћОЏОюОљОћ ОљОўОЋОъОЎОф ОћОЎОљ ОЌОЎОЕОЋОЉ ОъОЌОЊОЕ ОЕОю ОћОћОАОфОЉОеОЋОЎОЋОф ОћОюОюОЋ ОЉОћОЎОаОфОЪ ОћОДОЕОе ОћОЏОЎОъОЎ ОћОъОфОњОЉОЕ, ОъОбОЎОЎОЪ ОЎОЎОЕОЋОЮ ОЕОю ОЌОЋОД ОЉОЎОЎОА ОюОбОЋОюОЮ ОћОЏОЎОъОЎОћ ОћОДОЋОЋОаОўОЎОф, ОЏОљОЕОе ОћОаОфОЋОЪ ОћОЋОљ ОћОДОЕОе ОћОЏОЎОъОЎ.
ОфОЎОљОЋОе ОћОЏОюОљОф ОљОЋОеОЉОЎОўОюОЎОЮ ОъОЕОъОЕ ОюОћОЉОаОф ОћОДОЕОе ОЉОЎОЪ ОћОъОЉОаОћ ОћОњОљОЋОъОўОеОЎ ОЕОю ОћОъОЋОюОДОЋОюОћ, ОюОЉОЎОЪ ОцОбОеОЎ ОћОљОаОеОњОЎОћ ОЉОљОЋОеОЉОЎОўОюОЎОЮ ОћОљОюОДОўОеОЋОаОЎОЎОЮ ОЕОюОћ.
ОЏОюОюОЎ ОЎОАОЋОЊ ОюОЕОЎОъОЋОЕ ОЉОћОЏОюОљОћ ОљОЋОеОЉОЎОўОюОЎОф
ОћОЏОюОљОћ ОљОЋОеОЉОЎОўОюОЎОф ОЎОбОЎОюОћ ОъОљОЋОЊ ОЏОЕОъОЊОЋОЉОе ОЉОљОЋОеОЉОЎОўОюОЎОЮ ОћОъОфОДОЉОюОЎОЮ ОбОЉОЋОе ОљОюОДОўОеОЋОЪ ОюОЋ ОфОаОб ОќОЋОЋОЎОфОЎ ОаОъОЋОџ, ОЏОюОЋОъОе ОљОЋОеОЉОЎОўОюОЎ s ОЋОљОЋОеОЉОЎОўОюОЎ p.
ОЏОЊОЎ ОюОћОЎОбОќОе ОЉОћОЏОюОљОћ ОљОЋОеОЉОЎОўОюОЎОф ОюОћОЉОаОћ ОъОюОљОћ ОЕОю ОеОъОЋОф ОћОљОаОеОњОЎОћ ОЉОъОЋОюОДОЋОюОћ ОаОЊОеОЕ ОЎОЊОб ОъОбОъОЎОД ОЉОфОЋОеОф ОћОДОЋОЋОаОўОЎОЮ.
ОбОЮ ОќОљОф, ОаОЎОфОЪ ОюОћОЕОфОъОЕ ОЉОћ ОюОћОЉОаОф ОћОдОЋОеОћ ОћОъОЋОюОДОЋОюОеОЎОф, ОЋОћОЉОаОћ ОЌОюОДОЎОф ОЕОю ОеОъОЋОф ОћОљОаОеОњОЎОћ ОбОю ОцОЎ ОЏОъОћ ОЏОюОюОЎОЮ ОЉОАОЎОАОЎОЎОЮ:
- ОЏОЎОЋОЋОаОЎОЋОфОЋ ОЕОю ОЏОю ОљОўОЋОЮ ОЉОъОЋОюОДОЋОюОћ ОДОЋОЉОбОф ОљОф ОъОАОцОе ОћОљОЋОеОЉОЎОўОюОЎОЮ ОћОъОЋОЏОюОљОЎОЮ
- ОЏОљОЕОе ОЉОЏОю ОљОўОЋОЮ ОќОЋОњ ОљОюОДОўОеОЋОаОЎОЮ ОюОљ ОДОЋОЕОе ОъОЋОАОЎОБ ОюОЏОЎОЋОЋОаОЎОЋОф 1, ОЏОю ОДОЕОе ОЎОЌОЎОЊ ОЏОцОЋОю ОљОЋ ОъОЕОЋОюОЕ ОъОЋОАОЎОцОЎОЮ ОњОЮ ОћОЮ ОЏОю ОљОЌОЊ ОљОЌОф ОюОЏОЎОЋОЋОаОЎОЋОф. (ОюОъОЕОю ОЉОъОЋОюОДОЋОюОћ ОъОфОљОЪ CH4- ОюОцОЌОъОЪ ОЎОЕ ОљОеОЉОбОћ ОДОЕОеОЎОЮ ОюОЏОЪ ОЏОЎОЋОЋОаОЎОЋОфОЋ 4, ОЉОъОЋОюОДОЋОюОф ОћОъОЎОЮ H2O ОюОЌОъОдОЪ ОЎОЕОаОЮ ОЕОаОЎ ОќОЋОњОЋОф ОљОюОДОўОеОЋОаОЎОЮ ОюОљ ОДОЋОЕОеОЎОЮ ОЋОЕОаОЎ ОДОЕОеОЎОЮ ОюОЏОЪ ОЏОЎОЋОЋОаОЎОЋОфОЋ ОљОБ ОћОЎОљ 4. ОЉОъОЋОюОДОЋОюОф ОћОЌОаОДОЪ N2, ОюОЏОю ОљОўОЋОЮ ОЎОЕОаОЋ ОДОЕОе ОъОЕОЋОюОЕ ОљОЌОЊ ОЋОќОЋОњ ОљОюОДОўОеОЋОаОЎОЮ ОюОљ ОДОЋОЕОе ОљОЌОЊ, ОюОЏОЪ ОЏОЎОЋОЋОаОЎОЋОфОЋ ОфОћОЎОћ 2. ОћОћОЎОЉОеОЎОЊОЎОќОдОЎОћ ОЉОАОЋОцОЋ ОЕОю ОЊОЉОе ОћОЎОљ ОЏОќОЋ:
- (ОЏОЎОЋОЋОаОЎОЋОф ОцОЌОЋОф ОљОЌОЊ)├Ќ(ОљОЋОеОЉОЎОўОюОЎ P) + (ОљОЋОеОЉОЎОўОюОЎ S)
- ОДОЕОе ОЏОќОћ ОаОДОеОљ ОњОЮ ОДОЕОе ОАОЎОњОъОљ. ОЏОљОЕОе ОДОЕОе ОАОЎОњОъОљ ОаОЋОдОе ОеОД ОъОЌОцОЎОцОћ ОЉОЎОЪ ОљОЋОеОЉОЎОўОюОЎ s ОљОЋ ОъОЌОцОЎОцОћ ОЉОЎОЪ ОћОЏОюОљОћ ОЕОю ОљОЋОеОЉОЎОўОю s ОЋОљОЋОеОЉОЎОўОю p.
- ОЉОЏОю ОДОЕОе ОЏОцОЋОю ОЉОъОЋОюОДОЋОюОћ, ОћОДОЕОе ОћОЕОаОЎ ОъОЎОЎОдОњ ОљОЋОеОЉОЎОўОю ОъОЋОюОДОЋОюОеОЎ ОъОАОЋОњ ОљОЋОеОЉОЎОўОю ОцОљОЎ
- ОДОЕОе ОЏОќОћ ОаОДОеОљ ОњОЮ ОДОЕОе ОцОљОЎ. ОДОЕОе ОцОљОЎ ОаОЋОдОе ОеОД ОъОћОДОЉОюОћ ОЉОЎОЪ ОљОЋОеОЉОЎОўОюОЎ p.
ОЊОЋОњОъОћ: ОаОЎОфОЋОЌ ОћОћОЏОюОљОћ ОћОљОЋОеОЉОЎОўОюОЎОф ОЕОю ОљОўОЋОЮ ОцОЌОъОЪ ОЉОъОЋОюОДОЋОюОф ОљоХОфоХОЪ
 ОъОЋОюОДОЋОюОф ОљОфОЪ
ОъОЋОюОДОЋОюОф ОљОфОЪ
ОЊОЋОњОъОћ ОўОЋОЉОћ ОюОЏОџ ОћОЎОљ ОъОЋОюОДОЋОюОф ОћОљоХОфоХОЪ, ОЉОъОЋОюОДОЋОюОћ ОќОЋ ОЏОю ОљОўОЋОЮ ОцОЌОъОЪ ОаОДОЕОе ОюОЕОюОЕОћ ОљОўОЋОъОЎОЮ ОљОЌОеОЎОЮ ОъОЕОюОЋОЕОћ ОЏОЎОЋОЋОаОЎОЮ ОЕОЋОаОЎОЮ, ОюОЏОЪ ОЏОЎОЋОЋОаОЎОЋОфОЋ ОЕОюОЋОЕ, ОЏОюОЋОъОе ОбОюОЎОЋ ОюОћОЎОбОќОе ОЉОЕОюОЋОЕОћ ОљОЋОеОЉОЎОўОюОЎОЮ ОЋОЉОљОеОЉОбОћ ОљОюОДОўОеОЋОаОЎОЮ. ОбОЉОЋОе ОЏОю ОљОўОЋОЮ ОцОЌОъОЪ ОЎОЕОаОЮ ОЕОаОЎ ОДОЕОеОЎОЮ ОЎОЌОЎОЊОЎОЮ ОЋОДОЕОе ОЏОцОЋОю ОљОЌОЊ. ОћОДОЕОе ОћОЏОцОЋОю ОЌОЎОЎОЉ ОюОћОЎОЋОЋОдОе ОъОћОДОЉОюОћ ОЕОю ОљОЋОеОЉОЎОўОюОЎ ОцОљОЎ, ОЋОЕОаОЎ ОћОДОЕОеОЎОЮ ОћОЎОЌОЎОЊОЎОЮ ОаОЋОдОеОЎОЮ ОъОЌОцОЎОцОћ ОЉОЎОЪ ОљОЋОеОЉОЎОўОюОЎ ОАОЎОњОъОљ.
ОъОЉОў ОЉОўОЉОюОћ ОћОъОЌОќОЋОеОЎОф ОъОњОюОћ ОљОф ОћОћОбОеОЏОЋОф ОћОљОюОДОўОеОЋОаОЎОф ОЕОю ОљОўОЋОЮ ОцОЌОъОЪ ОЉОъОдОЉ ОћОЎОАОЋОЊ (ОюОљОеОЉОбОф ОћОљОюОДОўОеОЋОаОЎОЮ ОћОбОюОЎОЋОаОЎОЮ)-
- 2s22px12py12pz0
ОћОЏОЎОЋОЋОаОЎОЋОф 3 ОюОЏОЪ ОбОюОЎОаОЋ ОюОбОеОЉОЉ ОЕОюОЕОћ ОљОЋОеОЉОЎОўОюОЎОЮ, ОЏОљОЕОе ОюОцОЌОЋОф ОљОЌОЊ ОъОћОЮ ОЌОЎОЎОЉ ОюОћОЎОЋОф s, ОЋОбОю ОцОЎ ОћОаОЋОАОЌОћ: (ОћОЏОЎОЋОЋОаОЎОЋОф ОцОЌОЋОф ОљОЌОф)├Ќ(ОљОЋОеОЉОЎОўОюОЎ P) + (ОљОЋОеОЉОЎОўОюОЎS)
ОћОъОЊОЋОЉОе ОћОЋОљ ОЉОћОЏОюОљОћ ОЉОЎОЪ ОЕОаОЎ ОљОЋОеОЉОЎОўОюОЎ p ОЋОљОЋОеОЉОЎОўОю s ОљОЌОЊ, ОаОћОЋОњ ОюОАОъОаОћ ОЏ sp2.
ОаОЋОдОеОЋ ОЕОюОЋОЕОћ ОљОЋОеОЉОЎОўОюОЎОЮ ОЌОЊОЕОЎОЮ, ОЏОю ОљОЌОЊ ОъОћОЮ sp2. ОюОЎОЊОЎОбОф ОљОЏОюОЋОА ОћОљОюОДОўОеОЋОаОЎОЮ ОЉОћОЮ ОЎОЕ ОюОЊОбОф ОљОф ОњОЋОЉОћ ОћОљОаОеОњОЎОћ ОЕОюОћОЮ, ОЕОљОЋОфОћ ОаОЎОфОЪ ОюОљОъОЋОЊ ОЉОбОќОеОф ОЌОЎОЕОЋОЉОЎ ОфОЋОЌОюОф -
ОъОЕОДОюОЎ ОљОЋОеОЉОЎОўОюОЎ Оћ p ОћОЋОљ ОЕОаОЎ ОЕОюОЎОЕОЎОЮ, ОЋОъОЕОДОю ОљОЋОеОЉОЎОўОю Оћ s ОћОЋОљ ОЕОюОЎОЕ ОюОЏОЪ ОћОљОаОеОњОЎОћ ОЕОю ОћОљОЋОеОЉОЎОўОюОЎОЮ ОћОъОбОЋОеОЉОЉОЎОЮ ОћОЎОљ:
ОЕОюОЎОЕ ОъОћОљОаОеОњОЎОћ ОЕОю ОљОЋОеОЉОЎОўОю s ОЋОбОЋОЊ ОЕОаОЎ ОЕОюОЎОЕОЎОЮ ОъОћОљОаОеОњОЎОћ ОЕОю ОљОЋОеОЉОЎОўОю p.
ОЏОбОф ОаОЋОдОеОЋ ОЕОюОЋОЕОћ ОљОЋОеОЉОЎОўОюОЎ sp2 ОаОъОЋОЏОЎОЮ ОЉОљОаОеОњОЎОћ, ОЋОљОЋОеОЉОЎОўОю P ОљОЌОЊ ОаОЋОфОе ОъОбОюОЎОћОЮ ОЉОљОаОеОњОЎОћ, ОћОљОЏОюОЋОА ОћОЌОЊОЕ ОдОеОЎОџ ОюОћОЎОЋОф:
sp2 2 sp2 1 sp2 1 p 0, ОљОюОљ ОЕОЏОЊОЎ ОюОЎОдОЋОе ОљОф ОћОДОЕОеОЎОЮ ОљОЌОЊ ОћОљОюОДОўОеОЋОаОЎОЮ ОбОЋОЉОе ОбОЎОеОЋОе ОЋОћОфОЋОдОљОћ ОћОЎОљ sp2 1 sp2 1 sp2 1 p 1
ОюОЏОЪ ОъОдОљОаОЋ ОЉОъОЋОюОДОЋОюОф ОљоХОфоХОЪ ОАОЉОЎОЉ ОљОўОЋОЮ ОћОцОЌОъОЪ- 3 ОДОЕОеОЎ ОАОЎОњОъОљ, ОЏОю ОљОЌОЊ ОаОЋОдОе ОъОЌОцОЎОцОћ ОЕОю ОљОЋОеОЉОЎОўОюОЎ sp2.
ОЋОДОЕОе ОцОљОЎ ОљОЌОЊ, ОЕОаОЋОдОе ОъОћОДОЉОюОћ ОЉОЎОЪ ОЕОаОЎ ОљОЋОеОЉОўОюОЎ 2p. ОЋОЏОЪ ОаОЎОфОЪ ОюОћОбОеОЎОџ ОЉОдОЋОеОћ ОњОАОћ ОљОф ОћОъОљОќОЪ ОћОљОаОеОњОўОЎ ОъОћОћОЉОеОЎОЊОЎОќОдОЎОћ- ОюОцОаОЎ ОћОћОЎОЉОеОЎОЊОЎОќОдОЎОћ ОћОЎОЋ ОЕОаОЎ ОљОюОДОўОеОЋОаОЎОЮ ОЉОљОЋОеОЉОЎОўОю s ОЋ2 ОЉОљОЋОеОЉОЎОўОю p. ОљОЌОеОЎОћ ОћОЎОЋ 4 ОљОюОДОўОеОЋОаОЎОЮ ОЉОЕОаОЎ ОЕОюОЎОЕОЎОЮ ОћОЊОеОџ ОЉОЎОЪ ОљОЋОеОЉОЎОўОю s ОЋp. ОЏОюОЋОъОе 2 ОљОюОДОўОеОЋОаОЎОЮ ОўОЎОцОАОЋ ОЕОаОЎ ОЕОюОЎОЕОЎОЮ ОЕОю ОћОЊОеОџ, ОЋОЕОаОЎ ОљОюОДОўОеОЋОаОЎОЮ ОЎОеОЊОЋ ОЕОюОЎОЕ ОћОЊОеОџ, ОЏОюОЋОъОе ОЉОАОћ"ОЏ ОћОъОЋОюОДОЋОюОћ ОћОцОАОЎОЊОћ ОЏОъОЋОф ОљОаОеОњОЎОћ ОћОќОћОћ ОюОЕОаОЎ ОЕОюОЎОЕОЎОЮ ОцОбОе ОћОљОаОеОњОЎОћ ОЉОЎОЪ ОљОЋОеОЉОЎОўОюОЎ 2p Ою 2s.
(ОћОеОЋОЋОЌ ОћОљОаОеОњОўОЎ ОъОфОћОюОЎОџ ОќОћ, ОЎОфОњОюОћ ОЉОбОф ОЎОдОЎОеОф ОћОДОЕОе ОћОЏОЎОъОЎ ОљОќ ОЌОцОЎОцОф ОћОљОЋОеОЉОЎОўОюОЎОЮ ОфОћОцОЋОџ ОљОф ОћОфОћОюОЎОџ ОюОљОДОАОЋОфОеОъОЎ).
ОЏОюОюОЎ ОљОдОЉОб ОЕОю ОћОЏОюОљОф ОљОЋОеОЉОЎОўОюОЎОЮ
|
|
ОЎОЕ ОюОцОЕОў ОбОеОџ ОќОћ: ОћОбОеОџ ОъОаОЋОАОЌ ОЉОљОЋОцОЪ ОўОЏОаОЎ ОъОЊОЎ, ОЋОДОЕОћ ОюОћОЉОаОћ ОюОДОћОю ОћОеОЌОЉ.
|
| ОЎОЕ ОюОћОЋОАОЎОБ ОъОЉОЋОљ ОљОЎОаОўОЋОљОЎОўОЎОЉОЎ ОЕОЎОАОЉОЎОе ОљОф ОћОеОбОЎОЋОаОЋОф ОЋОћОъОЋОЕОњОЎОЮ ОЉОдОЋОеОћ ОцОЕОЋОўОћ ОЎОЋОфОе, ОеОдОЋОЎ ОЉОюОЎОЋОЋОЎ ОЊОЋОњОъОљОЋОф ОЋОфОЋОџ ОЕОЎОъОЋОЕ ОЉОљОъОдОбОЎОЮ ОљОЎОаОцОЋОњОеОцОЎОЎОЮ. ОљОЮ ОљОфОЮ ОАОЉОЋОеОЎОЮ ОЏОЎ ОћОбОеОџ ОљОЎОаОаОЋ ОЉОеОЋОе ОЊОЎОЋ ОљОЋ ОЕОЎОЕ ОаОДОЋОЊОћ ОЕОљОЎОаОЏОЮ ОъОЉОЎОаОЎОЮ ОЉОЋ, ОдОЎОЎОаОЋ ОќОљОф ОЉОЊОБ ОћОЕОЎОЌОћ ОЕОюОЋ. ОЎОЕ ОюОдОЎОЎОЪ ОЏОЎ ОбОеОЏОЎОЮ ОъОЊОбОЎОЎОЮ ОеОЉОЎОЮ ОъОдОеОЎОЏОЎОЮ ОеОДОб ОъОЋОДОЊОЮ.
|
|
| ОЎОЕ ОюОцОЕОў ОбОеОџ ОќОћ: ОћОбОеОџ ОъОаОЋОАОЌ ОЉОљОЋОцОЪ ОўОЏОаОЎ ОъОЊОЎ, ОЋОДОЕОћ ОюОћОЉОаОћ ОюОДОћОю ОћОеОЌОЉ.
|
| ОЎОЕ ОюОћОЋОАОЎОБ ОъОЉОЋОљ ОљОЎОаОўОЋОљОЎОўОЎОЉОЎ ОЕОЎОАОЉОЎОе ОљОф ОћОеОбОЎОЋОаОЋОф ОЋОћОъОЋОЕОњОЎОЮ ОЉОдОЋОеОћ ОцОЕОЋОўОћ ОЎОЋОфОе, ОеОдОЋОЎ ОЉОюОЎОЋОЋОЎ ОЊОЋОњОъОљОЋОф ОЋОфОЋОџ ОЕОЎОъОЋОЕ ОЉОљОъОдОбОЎОЮ ОљОЎОаОцОЋОњОеОцОЎОЎОЮ. ОљОЮ ОљОфОЮ ОАОЉОЋОеОЎОЮ ОЏОЎ ОћОбОеОџ ОљОЎОаОаОЋ ОЉОеОЋОе ОЊОЎОЋ ОљОЋ ОЕОЎОЕ ОаОДОЋОЊОћ ОЕОљОЎОаОЏОЮ ОъОЉОЎОаОЎОЮ ОЉОЋ, ОдОЎОЎОаОЋ ОќОљОф ОЉОЊОБ ОћОЕОЎОЌОћ ОЕОюОЋ. ОЎОЕ ОюОдОЎОЎОЪ ОЏОЎ ОбОеОЏОЎОЮ ОъОЊОбОЎОЎОЮ ОеОЉОЎОЮ ОъОдОеОЎОЏОЎОЮ ОеОДОб ОъОЋОДОЊОЮ.
|
ОЕОЎОъОЋОЕ ОцОЕОЋОў ОЉОфОЋОдОљОЋОф ОЕОю ОћОфОЋОеОћ ОаОбОќОе ОЉОЏОюОюОЎ ОљОдОЉОб ОЕОю ОћОЏОюОљОћ ОљОЋОеОЉОЎОўОюОЎОф:
- ОЌОЋОД ОЕОЎОъОЋОе ОћОљОЋОеОЉОЎОўОюОЎОЮ - ОъОАОцОе ОћОљОЋОеОЉОЎОўОюОЎОЮ ОћОъОбОЋОеОЉОЉОЎОЮ ОћОЋОљ ОъОАОцОе ОћОљОЋОеОЉОЎОўОюОЎОЮ ОЕОаОЋОдОеОЋ. ОЉОЊОЋОњОъОф ОћОљОфОЪ, ОбОюОЎОаОЋ ОюОЎОдОЋОе ОЕОюОЋОЕОћ ОљОЋОеОЉОЎОўОюОЎОЮ, ОюОЏОЪ ОаОбОеОЉОЉ ОЕОюОЋОЕОћ ОљОЋОеОЉОЎОўОюОЎОЮ. ОЌОЋОД ОќОћ ОаОЏОЋОЪ ОъОАОЎОЉОЋОф ОЌОЎОЕОЋОЉОЎОЋОф: ОЏОю ОљОЋОеОЉОЎОўОю ОћОЋОљ ОЉОбОдОЮ ОЋОДОўОЋОе ОбОдОъОЎ ОЕОю ОћОћОъОЎОюОўОЋОаОЎОљОЪ ОЕОю ОћОъОЋОюОДОЋОюОћ, ОћОъОЎОюОўОЋОаОЎОљОЪ ОќОћ ОаОцОеОЕ ОбОю ОЉОАОЎОА ОЕОбОЋОдОъОфОЋ ОЏОбОЋОдОъОф ОћОљОЋОеОЉОЎОўОюОЎОЮ ОћОъОбОЋОеОЉОЉОЎОЮ, ОЋОЏОЎОЋОЋОЪ ОЕОюОъОўОеОЎОдОћ ОћОеОъОЎОўОЎОф nXn ОЎОЕ n ОЋОДОўОЋОеОЎОЮ ОбОдОъОЎОЎОЮ, ОъОАОцОе ОћОЋОЋОДОўОЋОеОЎОЮ ОћОбОдОъОЎОЎОЮ ОЕОЋОЋОћ ОюОъОАОцОе ОЋОДОўОЋОеОЎ ОћОЉОАОЎОА.
- ОћОЏОЎОЋОЋОаОЎОЋОф ОћОЎОљ ОАОЏОЋОЮ ОћОъОбОеОЎОЏОЎОЮ - ОъОЏОЎОЋОЋОЪ ОЕОаОћОЋОњ ОюОЏОфОЋОЉ ОљОф ОъОАОцОе ОћОљОЋОеОЉОЎОўОюОЎОЮ ОћОъОбОЋОеОЉОЉОЎОЮ ОЉОЏОфОЉ ОбОЎОюОЎ (ОюОъОЕОю ОЉОЊОЋОњОъОћ ОЕОю ОљОфОЪ ОЕОаОЎ ОљОЋОеОЉОЎОўОюОЎ p ОЋОљОЋОеОЉОЎОўОю s ОаОЏОфОЉОЎОЮ ОЏ: sp2) ОДОю ОюОАОЏОЋОЮ ОљОф ОћОъОАОцОеОЎОЮ ОЉОЏОфОЉ ОћОбОЎОюОЎ, ОЋОАОЏОЋОЮ ОќОћ ОдОеОЎОџ ОюОћОЎОЋОф ОЕОЋОЋОћ ОюОЏОЎОЋОЋОаОЎОЋОф. ОюОЊОЋОњОъОћ ОЉОъОДОеОћ ОЕОю ОљОфОЪ, sp2, Оћ"ОъОбОеОЎОџ" ОЕОю s ОћОЋОљ 1, Оћ"ОъОбОеОЎОџ" ОЕОю p ОћОЋОљ 2 ОюОЏОЪ 2+1=3, ОћОЎОЉОеОЎОЊОЎОќОдОЎОћ ОќОЋ ОўОЋОЉОћ ОюОЏОю ОљОўОЋОЮ ОЉОбОю ОЏОЎОЋОЋОаОЎОЋОф 3.
- ОћОљОаОеОњОЎОћ ОъОдОЎОЎОфОф ОюОЌОЋОД ОћОъОаОЋОБ - ОћОљОЋОеОЉОЎОўОюОЎОЮ ОћОЌОЊОЕОЎОЮ ОаОъОдОљОЎОЮ ОЉОфОЋОЋОџ ОЉОЎОЪ ОћОљОЋОеОЉОЎОўОюОЎОЮ ОћОЎОЕОаОЎОЮ, ОЋОДОеОЋОЉ ОЎОЋОфОе ОюОљОЋОеОЉОЎОўОю ОъОъОаОЋ ОбОеОЉОЉОаОЋ ОЎОЋОфОе, ОЉОЎОЌОА ОЎОЕОе. ОюОъОЕОю, ОЉОЊОЋОњОъОћ ОЕОю ОљОфОЪ ОбОеОЉОЉОаОЋ ОЕОюОЕОћ ОљОЋОеОЉОўОюОЎОЮ ОюОЏОЪ ОбОюОЎОаОЋ ОюОЌОюОД ОљОф ОћОцОбОе ОюОЕОюОЕ ОЎОЌОЎОЊОЋОф. ОћОЎОЌОА ОЉОЎОЪ ОћОљОЋОеОЉОўОюОЎОЮ ОћОЎОЕОаОЎОЮ ОћОЎОћ 1:2 ОљОЋОеОЉОЎОўОюОЎ s:p, ОюОЏОЪ ОњОЮ ОћОљОаОеОњОЎОћ ОаОъОдОљОф ОЉОЕОаОЎ ОЕОюОЎОЕОЎОЮ ОћОцОбОе ОЉОЎОЪ s Оюp. ОЌОЋОД ОћОъОаОЋОБ ОъОЕОъОЕ ОЉОъОДОеОћ ОќОћ ОъОЕОЋОЮ ОЕОћОЋОљ ОћОдОњОћ ОљОЌОеОф ОЕОю ОЌОЎОЕОЋОЉ ОфОЋОЌОюОф.
ОДОЎОЕОЋОеОЎОЮ ОЌОЎОдОЋОаОЎОЎОЮ