גאומטריה דיפרנציאלית
|
Read other articles:

Asosiasi Sepak Bola Saint Kitts dan NevisCONCACAFDidirikan1932Kantor pusatBasseterreBergabung dengan FIFA1992Bergabung dengan CONCACAF1990 (anggota rekan)1992PresidenAnthony JohnsonWebsitehttp://www.sknfa.com Asosiasi Sepak Bola Saint Kitts dan Nevis (Inggris: St. Kitts and Nevis Football Associationcode: en is deprecated ) adalah badan pengendali sepak bola di Saint Kitts dan Nevis. Kompetisi Badan ini menyelenggarakan beberapa kompetisi di Saint Kitts dan Nevis, termasuk Liga Utama SKNFA ya...

عبد الأمير الجمري الشيخ عبد الأمير الجمري معلومات شخصية الميلاد 1 مارس 1938(1938-03-01)بني جمرة - البحرين تاريخ الوفاة 18 ديسمبر 2006 (عن عمر ناهز 68 عاماً) سبب الوفاة نوبة قلبية، وقصور كلوي الجنسية بحريني اللقب أبا جميل الأولاد جميل و منصور و صادق و محمد حسين و لؤي و علي و مهدي...

Kereta api SiliwangiKereta api Siliwangi di Stasiun CianjurInformasi umumJenis layananKereta Api lokalStatusBeroperasiDaerah operasiDaerah Operasi I JakartaPendahuluKA Lokal Cianjuran atau KA Argo Peuyeum (Bisnis/Ekonomi)Mulai beroperasi 8 Februari 2014; 10 tahun lalu (2014-02-08) (sebagai kereta api aglomerasi) 19 Februari 2016; 8 tahun lalu (2016-02-19) (sebagai kereta api lokal) Operator saat iniKereta Api IndonesiaLintas pelayananStasiun awalSukabumiJumlah pemberhentianLihatlah ...

Štiavnické vrchy Protected Landscape AreaCHKO Štiavnické vrchyIUCN category V (protected landscape/seascape)Sitno CastleLocationSouthern central SlovakiaCoordinates48°32′N 18°58′E / 48.533°N 18.967°E / 48.533; 18.967Area776.30 km2 (299.7 mi2)Established22 September 1979Governing bodySpráva CHKO Štiavnické vrchy (Štiavnické vrchy PLA administration) in Banská Štiavnica Štiavnické vrchy Protected Landscape Area (Slovak: Chránená krajinná obla...

Variety of grassland ecosystems found in the Pannonian Basin The Pannonian steppe in Seewinkel, Austria A typical draw well in the Pannonian steppe in Hortobágy National Park Hortobágy National Park The Pannonian Steppe[1] is a variety of grassland ecosystems[2] found in the Pannonian Basin. It is an exclave of the Great Eurasian Steppe, found in modern-day Austria, Bulgaria, Hungary, Romania, Serbia, Slovakia and easternmost parts of Croatia.[3][4] Geography...
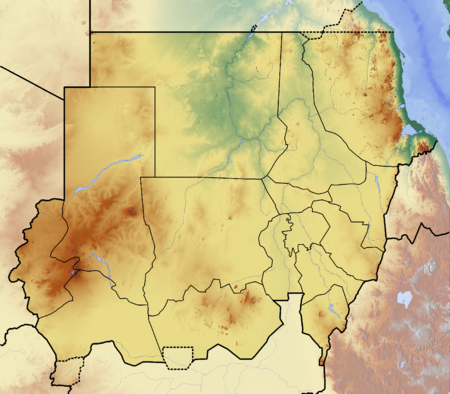
لمعانٍ أخرى، طالع السودان (توضيح). جمهورية السودان جمهورية السودان السودانعلم السودان السودانشعار السودان الشعار الوطنيالنصر لنا النشيد: نحن جند الله جند الوطن الأرض والسكان إحداثيات 15°N 32°E / 15°N 32°E / 15; 32 [1] أعلى قمة جبل مرة (3,042 متر...

Shopping mall in Visakhapatnam, IndiaCMR CentralLocationMaddilapalem, Visakhapatnam, IndiaCoordinates17°44′03″N 83°19′06″E / 17.734111°N 83.318264°E / 17.734111; 83.318264Opening dateJanuary 2010OwnerCMRNo. of floors6Parking2-level basement parkingWebsitecmrcentral.com CMR Central is a shopping mall located at Maddilapalem, Visakhapatnam. It was developed by CMR Shopping Mall Private Limited.[1][2] Description Renowned as one of the biggest...

1995 rocket attacks on Croatian cities during the Croatian War of Independence For the 1991 air strike on Zagreb, see Bombing of the Banski Dvori. Zagreb rocket attacksThe body of Ana Mutevelić lying on the intersection of Vlaška and Draškovićeva streetsLocationZagreb, CroatiaDate2–3 May 1995TargetDowntown ZagrebZagreb AirportAttack typeArtillery rocket attackWeapons262 mm M-87 Orkan multiple rocket launcher armed with cluster bombsDeaths7Injured214[1]PerpetratorsArmy of the Rep...

Brazilian footballer and manager Moisés Personal informationFull name Moisés Matias de AndradeDate of birth (1948-01-10)January 10, 1948Place of birth Resende, BrazilDate of death August 26, 2008(2008-08-26) (aged 60)Place of death Rio de Janeiro, BrazilPosition(s) DefenderSenior career*Years Team Apps (Gls)1966–1968 Bonsucesso 1968 Flamengo 1968 Bonsucesso 1969–1971 Botafogo 1971–1976 Vasco da Gama 220[1] (3)1976–1978 Corinthians 122 (0)1978 Paris Saint-Germain 1978 Fl...

Indian politician Riti PathakMember of the Madhya Pradesh Legislative AssemblyIncumbentAssumed office 3 December 2023Preceded byKedarnath ShuklaConstituencySidhiMember of Parliament, Lok SabhaIn office16 May 2014 – 6 December 2023[1][2]Preceded byGovind Prasad MishraSucceeded byVacantConstituencySidhi Personal detailsBorn (1977-07-01) 1 July 1977 (age 46)Khatkhari, Madhya Pradesh, IndiaPolitical partyBharatiya Janata PartySpouseShri Rajnish PathakChildren2P...

Species of dragonfly Orthetrum julia Male, uMkhuze Game Reserve, KwaZulu Natal, South Africa Female, Ithala Game Reserve, KwaZulu Natal, South Africa Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Odonata Infraorder: Anisoptera Family: Libellulidae Genus: Orthetrum Species: O. julia Binomial name Orthetrum juliaKirby, 1900 Orthetrum julia, the Julia skimmer is a species o...

Ministry of Transport (運輸省, Un'yu-shō) was a ministry of the Japanese government. It managed 849 public corporations before its 2001 merger. It merged into the Ministry of Land, Infrastructure, Transport and Tourism (MLIT) in January 2001.[1] References ^ Carpenter, Susan. Why Japan Can't Reform: Inside the System. Palgrave Macmillan/Springer Publishers, 2008. ISBN 0230595065, 9780230595064. p. 12. Same content appears in: Carpenter, Susan. Japan's Nuclear Crisis: The Rout...

Shotgun with two parallel barrels This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2023) (Learn how and when to remove this message) A view of the break-action of a typical side-by-side (SxS) double-barreled shotgun, with the Anson & Deeley boxlock action open and the extractor visible. The lever and the safety catch can also be clearly seen. A view ...

Elezione dei delegati della XIII Assemblea nazionale del popoloStato Cina LegislaturaXIII Leader Xi Jinping Wu Weihua Ding Zhongli Partiti Partito Comunista Cinese Società 3 Settembre Lega Democratica Cinese Voti -71,11% -2,15% Seggi 2 119 / 2 980 64 / 2 980 58 / 2 980 Differenza % 1,10% 2,15% 1,95% presidente elettoLi Zhanshu XII XIV Elezioni presidenziali in Cina del 2018 (presidente)Stato Cina Data17 marzo Eletto Xi JinpingPartito Partito Comunista Cine...
51st season in franchise history 2010 Buffalo Bills seasonOwnerRalph WilsonGeneral managerBuddy NixHead coachChan GaileyHome fieldRalph Wilson StadiumRogers Centre (Week 9)ResultsRecord4–12Division place4th AFC EastPlayoff finishDid not qualify Pro BowlersDT Kyle Williams ← 2009 Bills seasons 2011 → The 2010 season was the Buffalo Bills' 51st season in the National Football League (NFL), It was Buffalo's first season with Buddy Nix in the role of general manager a...

Raymond GlendenningBornRaymond Carl Glendenning(1907-09-25)25 September 1907Newport, Monmouthshire, WalesDied23 February 1974(1974-02-23) (aged 66)Buckinghamshire, EnglandOccupationSports commentator Raymond Carl Glendenning (25 September 1907 – 23 February 1974) was a BBC radio sports commentator and occasional character actor. Early years Glendenning was born in Newport, Monmouthshire, Wales, son of Robert James Samuel Glendenning, a commercial clerk and later a company director, an...

Baby daughter of Nero and Poppaea Sabina Claudia AugustaAugustaCLAVDIAStatue believed to possibly depict an older idealized Claudia.BornClaudiaCitizenshipRomanEraNeronianKnown forDaughter of Roman emperor NeroParentsNero (father)Poppaea Sabina (mother)FamilyJulio-ClaudianHonoursAugusta Claudia Augusta (Classical Latin: [ˈklau̯dɪ.a]; January 63 – May 63) was the only daughter[1] of the Roman Emperor Nero and his second wife, the Roman Empress Poppaea Sabina. Claudia a...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Asosiasi DPRD Kabupaten Seluruh Indonesia – berita · surat kabar · buku · cendekiawan · JSTOR Asosiasi DPRD Kabupaten Seluruh Indonesia ( “ADKASI” ) merupakan organisasi yang anggotanya adalah DPRD K...

Paul Antoine FleuriotVicomte de LangleMiniature portrait of Fleuriot de LangleNickname(s)Fleuriot de LangleBorn(1744-08-01)1 August 1744Kerlouët Castle, FranceDied11 December 1787(1787-12-11) (aged 43)Tutuila, SamoaBuriedChoir of Saint-Louis Church, BrestAllegianceKingdom of FranceService/branchFrench Royal NavyYears of service1758 – 1787RankRear-AdmiralCommands heldExperimentAstréeAstrolabeBattles/warsHudson Bay expeditionAwardsKnight of the Order of Saint LouisSociety of the C...

Electronic document used to prove the ownership of a public key In cryptography, a public key certificate, also known as a digital certificate or identity certificate, is an electronic document used to prove the validity of a public key.[1][2] The certificate includes the public key and information about it, information about the identity of its owner (called the subject), and the digital signature of an entity that has verified the certificate's contents (called the issuer). ...











