בדיקת יתירות מחזורית

בדיקת יתירות מחזורית (באנגלית: Cyclic redundancy check, או בקיצור CRC) היא סוג של קוד לאיתור שגיאות המשמש לאיתור שגיאות בהעברת נתונים.

לפני העברת המידע מחושב ה־CRC ומתווסף למידע המועבר. לאחר העברת המידע, הצד המקבל מאשר באמצעות ה־CRC שהמידע הועבר ללא שינויים.

השימוש ב־CRC נפוץ בעיקר בשל קלות המימוש שלו בחומרה בינארית, קלות החישוב המתמטית שלו, ובמיוחד היעילות שלו בגילוי שגיאות נפוצות הנובעות כתוצאה מערוצי תקשורת רועשים.

מבוא

CRC מבוסס על תאוריה של קוד מחזורי (מעגלי) לתיקון שגיאות. השימוש בקוד מחזורי שיטתי, אשר מקודד הודעות על ידי הוספה של ערך בדיקה עם גודל קבוע, בשביל איתור שגיאות ברשתות תקשורת. CRC הוצג לראשונה על ידי וו. ווסלי פטרסון ב-1961. קודים מחזוריים הם לא רק פשוטים למימוש, אלא הם גם טובים במיוחד לאיתור פרצי שגיאות בהודעות עם נתונים אשר נשלחות ברצף. זה חשוב בגלל שפרצי שגיאות הם בעיות העברה נפוצות בערוצי תקשורת, אשר כוללים התקני אחסון מגנטיים ואופטיים.

סיביות טיפוסי אשר מוצמד לבלוק מידע באורך שרירותי יאתר כל שגיאת פתע שאינה גדולה מ- סיביות ויאתר כמות של מפרצי שגיאות הגדולות מ- סיביות.

אפיון של קוד CRC דורש הגדרה של מה שנקרא פולינום יוצר. הפולינום הזה נעשה מחלק של ה-polynomial long division, אשר לוקח את ההודעה כמחולקת ומחסיר את המנה והיתרה היא התוצאה. האזהרה החשובה היא כאשר המקדם הפולינומי שחושב בהתאם לשדה הסופי האריתמטי, כך שפעולה נוספת יכולה לממש רוחב בתים מקבלים (אין משיכה בין ספרות). הגודל של השארית הוא תמיד נמוך מהגודל של המחולל הפולינומי, אשר ממחיש כמה גדולה התוצאה יכולה להיות.[1]

למעשה, כל השימושים הנפוצים ב-CRC משתמשים בשדה סופי של שני אלמנטים. שני האלמנטים בדרך כלל נקראים 1 ו-0, שבאופן נוח ביותר תואם לארכיטקטורה של המחשב.

CRC נקרא n-bit כאשר ערך הבדיקה בגודל n-bit. ל-n נתון, יש מספר CRC אפשריים, כל אחד כזה בפולינום שונה לפולינום כזה יכול להיות n כמעלה הגבוהה ביותר, כלומר n+1 ביטויים. במילים אחרות, לפולינום בגודל של n+1, הקידוד שלו דורש n+1  בתים. רוב הפולינומים מאפיינים ירידה בביט של ה-MSB או LSB, מכיוון שהם תמיד 1. ל-CRC והפולינום המקושר יש שם במבנה הזה  CRC-n-XXX.

מערכת איתור הבעיות הפשוטה ביותר, סיבית זוגיות, הוא למעשה CRC של 1-bit. הפולינום המתאים הוא x+1 (שני ביטויים) ושמו הוא CRC-1.

אופן הפעולה

CRC מבוסס על האיזומורפיזם שבין וקטורים לפולינומים, כך שמסתכלים על כל וקטור באורך n כפולינום שמקדמיו הם קואורדינטות הווקטור. CRC משתמש בפולינום המוגדר בפולינום יוצר מדרגה r. סוגים שונים של קוד CRC משתמשים בפולינומים יוצרים שונים.

בהינתן פולינום יוצר מדרגה r ובהינתן הודעה M שברצוננו לקדד, עלינו לבצע את הפעולות הבאות:

  1. נוסיף r אפסים מימין להודעה.
  2. נחלק בפולינום (תוך שימוש בחילוק של השדה מודולו 2)
  3. נחסר את השארית תוך שימוש ב-xor במקום בחיסור רגיל.

נצרף את התוצאה שקיבלנו מימין להודעה המקורית ונשלח.

כמו בכל קידוד Checksum, הצד המקבל יבצע את שלבים 1 ו-2 ויוודא ש-r הביטים האחרונים שנשלחו זהים לתוצאה שהתקבלה.

ראו גם

קישורים חיצוניים

הערות שוליים

  1. ^ Peterson, W. W. and Brown, D. T, Cyclic Codes for Error Detection, Proceedings of the IRE 49 49(1), עמ' 228-235

Read other articles:

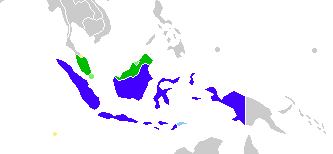
List of countries and territories where Malay is an official language

The following is a list of sovereign states that have Malay as an official language. Malay Linguasphere.   Indonesia   Malaysia   Singapore and Brunei, where Standard Malay is an official language   East Timor, where Indonesian is a working language   Southern Thailand and the Cocos Isl., where other varieties of Malay are spoken Sovereign states Countries where Malay is a de jure official language Country Region Population1 Primary Language?...

 

 

Akhir Perang Dunia II di Eropa

Halaman depan The Montreal Daily Star mengumumkan penyerahan Jerman. Akhir Perang Dunia II di Eropa merupakan pertempuran terakhir dari Teater Eropa pada saat Perang Dunia II serta menyerahnya Jerman pada akhir April dan awal Mei 1945. Garis Waktu Pada tanggal 8 Mei 1945 di Berlin-Karlshort, komandan tempur Wilhelm Keitel menandatangani surat kapitulasi tanpa syarat. Ketika Hitler ditemukan telah tewas, Perang Dunia II di Eropa telah usai, Nazi yang mendominasi Jerman dan Eropa telah diguling...

 

 

Oshi ga Budōkan Ittekuretara Shinu

Oshi ga Budōkan Ittekuretara Shinu推しが武道館いってくれたら死ぬ MangaPengarangAuri HiraoPenerbitTokuma ShotenMajalahMonthly Comic RyūDemografiSeinenTerbit19 Juni 2015 – sekarangVolume10 Seri animeSutradaraYusuke YamamotoSkenarioDeko AkaoMusikMoe HyūgaStudioEight BitSaluranasliTBS, BS-TBSTayang 9 Januari 2020 – 26 Maret 2020Episode12  Portal anime dan manga Oshi ga Budōkan Ittekuretara Shinu (推しが武道館いってくれたら死ぬcode: ja is deprecated ,...

تطورية

التطورية (قابلية التطور-evolvability) هي مفهوم في علم الأحياء التطوري الذي يحاول قياس قدرة الكائنات الحية على التطور.[1][2][3] على الرغم من عدة تعاريف ممكنة، التطورية على نطاق واسع هي قدرة الكائنات الحية على توليد التنوع الجيني من خلال تطور الانتقاء الطبيعي، ليكون أفضل...

 

 

Gita Gutawa

Gita GutawaGita pada konser Kotak musik Gita Gutawa tahun 2010LahirAluna Sagita Gutawa11 Agustus 1993 (umur 30)Jakarta, IndonesiaNama lainGita GutawaAlmamater University of Birmingham London School of Economics and Political Science PekerjaanAktrisModelPenulis laguPenyanyiTahun aktif2005 - sekarangTinggi155 cm (5 ft 1 in)Orang tuaErwin Gutawa (ayah) Lutfi Andriani (ibu)KerabatAura Aira Gutawa (adik)Karier musikGenrePopTeater musikalKlasikPop remajaPop rockSerios...

 

 

Franz Liszt

Vous lisez un « bon article » labellisé en 2007. « Liszt » redirige ici. Pour les autres significations, voir Liszt (homonymie). Franz Liszt Franz Liszt en 1858. Données clés Nom de naissance Liszt Ferenc Naissance 22 octobre 1811 Doborján, Hongrie( Empire d'Autriche) Décès 31 juillet 1886 (à 74 ans) Bayreuth, Bavière( Empire allemand) Activité principale Compositeur, pianiste et chef d'orchestre Style Musique romantique Activités annexes Écrivain...

Satuan Karya Pramuka

Satuan Karya Pramuka (Saka) adalah wadah pendidikan guna menyalurkan minat, mengembangkan bakat, meningkatkan pengetahuan, kemampuan, keterampilan dan pengalaman para Pramuka dalam berbagai bidang kejuruan serta memotivasi mereka untuk melaksanakan kegiatan nyata dan produktif sehingga dapat memberi bekal bagi kehidupannya dan pengabdiannya pada masyarakat, bangsa, dan negara sesuai aspirasi pemuda Indonesia dan tuntutan perkembangan pembangunan dalam rangka peningkatan pertahanan Nasional. S...

 

 

Meet the Parents

Meet the ParentsSutradaraJay RoachProduserRobert De NiroJay RoachJane RosenthalNancy TenenbaumSkenarioJohn Hamburg, James HerzfeldBerdasarkanCerita asli:Greg Glienna & Mary Ruth ClarkePemeranBen StillerRobert De NiroTeri PoloBlythe Dannerdan Owen WilsonPenata musikRandy NewmanSinematograferPeter JamesPenyuntingJon PollPerusahaanproduksiTriBeCa ProductionsDistributor- AS -Universal Studios- Internasional -DreamWorks PicturesTanggal rilis 6 Oktober 2000 (2000-10-06) Durasi108 men...

 

 

Mia Wasikowska

Mia WasikowskaPada the Independent Spirit Awards di Los Angeles pada tanggal 5 Maret 2010PekerjaanAktrisTahun aktif2004–sekarang Mia Wasikowska (pengucapan bahasa Inggris: [ˌvɑːʃiːˈkɒfskə] VAH-shee-KOF-skə;[1][2] lahir 25 Oktober 1989) adalah seorang pemeran perempuan asal Australia. Ia berperan sebagai Alice dalam film Alice in Wonderland.(Alice Throught The Looking Glass Film 2016) Filmografi Televisi Tahun Produksi Peran Catatan 2004 All Saints Lily Wa...

大字 (数字)

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています（詳細）。 数字の大字（だいじ）は、漢数字の一種。通常用いる単純な字形の漢数字（小字）の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券（「壱」が大字） 弐千円日本銀行券（「弐」が大字） 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

 

 

中華民國—瑞士關係

  提示：此条目页的主题不是中國—瑞士關係。   關於中華民國與「瑞」字國家的外交關係，詳見中瑞關係 (消歧義)。 中華民國—瑞士關係 中華民國 瑞士 代表機構駐瑞士台北文化經濟代表團瑞士商務辦事處代表代表 黃偉峰 大使[註 1][4]處長 陶方婭[5]Mrs. Claudia Fontana Tobiassen 中華民國—瑞士關係（德語：Schweizerische–republik china Beziehungen、法�...

 

 

1993 Detroit Lions season

NFL team season 1993 Detroit Lions seasonOwnerWilliam Clay Ford Sr.General managerChuck SchmidtHead coachWayne FontesHome fieldPontiac SilverdomeResultsRecord10–6Division place1st NFC CentralPlayoff finishLost Wild Card Playoffs(vs. Packers) 24–28 ← 1992 Lions seasons 1994 → The 1993 season was the Detroit Lions' 64th season in the National Football League (NFL), their 60th In Detroit, and their fifth under the head coach Wayne Fontes.The Lions improved upon the...

Loris Capirossi

Loris Capirossi Biographie Surnom Capirex Date de naissance 4 avril 1973 (51 ans) Lieu de naissance Castel San Pietro Terme (province de Bologne) Nationalité Italie Carrière professionnelle Années d'activité 1990 - 2011 Statistiques Course Pole Vic. Pod. MotoGP 158 8 7 26 500 cm3 59 5 2 16 250 cm3 84 23 12 37 125 cm3 27 5 8 20 Palmarès 1er 2e 3e MotoGP ' - 1 500 cm3 ' - 1 250 cm3 1 1 2 125 cm3 2 - - modifier  Loris Capirossi, surnommé Capirex, es...

 

 

哥伦布 (密西西比州)

密西西比州 哥伦布城市綽號：Possum Town哥伦布位于密西西比州的位置坐标：33°30′06″N 88°24′54″W / 33.501666666667°N 88.415°W / 33.501666666667; -88.415国家 美國州密西西比州县朗兹县始建于1821年政府 • 市长罗伯特·史密斯 (民主党)面积 • 总计22.3 平方英里（57.8 平方公里） • 陸地21.4 平方英里（55.5 平方公里） • ...

 

 

Monument Park (Yankee Stadium)

Open-air museum in Yankee Stadium Monument ParkMonument Park at Yankee StadiumLocation1 East 161st StreetYankee StadiumThe Bronx, New YorkCoordinates40°49′47.22″N 73°55′31.7″W / 40.8297833°N 73.925472°W / 40.8297833; -73.925472FounderNew York Yankees Monument Park is an open-air museum located in Yankee Stadium in the Bronx, New York City. It contains a collection of monuments, plaques, and retired numbers honoring distinguished members of the New York Yank...

خواكين إيبارا

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2019) خواكين إيبارا معلومات شخصية الميلاد 20 يوليو 1726   سرقسطة  الوفاة 13 سبتمبر 1785 (59 سنة)   مدريد  مواطنة إسبانيا  الحياة العملية المهنة طابع حروف  ...

 

 

Jeh Johnson

4th US Secretary of Homeland Security and lawyer Jeh JohnsonOfficial portrait, 20144th United States Secretary of Homeland SecurityIn officeDecember 23, 2013 – January 20, 2017PresidentBarack ObamaDeputyAlejandro MayorkasPreceded byJanet NapolitanoSucceeded byJohn F. KellyGeneral Counsel of the Department of DefenseIn officeFebruary 10, 2009 – December 31, 2012PresidentBarack ObamaPreceded byWilliam J. Haynes IISucceeded byStephen W. PrestonGeneral Counsel of the Air For...

 

 

Astéroïdes troyens de Mars

Les groupes de troyens L5 (vert) et L4 (bleu clair) des troyens de Mars et de Jupiter avec les orbites des deux planètes. Mars est représentée en rouge et Jupiter en gris sur l'orbite externe. Les astéroïdes troyens de Mars sont un groupe d'astéroïdes qui partagent l'orbite de la planète Mars, aux alentours des points de Lagrange L4 et L5 du système Soleil-Mars situés respectivement 60° en avance ou 60° en retard sur Mars. Au 2 avril 2024, le Centre des planètes mineures rec...

INORAN

INORAN 2013年のシンガポール公演にて基本情報出生名 井上清信別名 イノラン生誕 (1970-09-29) 1970年9月29日（54歳）出身地 日本・神奈川県秦野市ジャンル ロックオルタナティヴ・ロックガレージ・ロックシューゲイザードリーム・ポップアンビエント職業 ミュージシャンシンガーソングライター音楽プロデューサーモデル担当楽器 ボーカルギターレーベル KING RECORDS共同作業...

 

 

Coppa Latina 1952

Questa voce o sezione sull'argomento edizioni di competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Coppa Latina 1952 Competizione Coppa Latina Sport Calcio Edizione 4ª Date dal 25 giugno 1952al 29 giugno 1952 Luogo  Francia Parigi Partecipanti 4 Formula Eliminazione di...