ОљОеОЎОЌОЎ ОЋОљОаОњ
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2017. Kota Hattori Informasi pribadiNama lengkap Kota HattoriTanggal lahir 22 November 1977 (umur 46)Tempat lahir Prefektur Chiba, JepangPosisi bermain GelandangKarier senior*Tahun Tim Tampil (Gol)1996-2011 Sanfrecce Hiroshima 2012 Fagiano Okayama * Penam...

Bagian dari seriIslam Rukun Iman Keesaan Allah Malaikat Kitab-kitab Allah Nabi dan Rasul Allah Hari Kiamat Qada dan Qadar Rukun Islam Syahadat Salat Zakat Puasa Haji Sumber hukum Islam al-Qur'an Sunnah (Hadis, Sirah) Tafsir Akidah Fikih Syariat Sejarah Garis waktu Muhammad Ahlulbait Sahabat Nabi Khulafaur Rasyidin Khalifah Imamah Ilmu pengetahuan Islam abad pertengahan Penyebaran Islam Penerus Muhammad Budaya dan masyarakat Akademik Akhlak Anak-anak Dakwah Demografi Ekonomi Feminisme Filsafat...

Victoria SilvstedtLahirKaren Victoria Silvstedt19 September 1974 (umur 49)Skellefte├Ц, SwediaTahun aktif1993-sekarangInformasi modelingTinggi179 cm (5 ft 10 in)Warna rambutpirangWarna matabiru Situs webhttp://victoriasilvstedt.com Karen Victoria Silvstedt (lahir 19 September 1974) adalah peragawati, aktris, penyanyi dan kepribadian televisi Swedia. Awal kehidupan Lahir di Skellefte├Ц, Victoria Silvstedt dibesarkan dalam keluarga lima di Bolln├цs, memiliki satu kakak ...

German single-seat glider, 1994 This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (December 2012) (Learn how and when to remove this template message) Ventus-2 Ventus 2b being winch-launched at Lasham airfield Role 15 metre-class and 18 metre-class sailplaneType of aircraft National origin Germany Manufacturer Schempp-Hirth First flight 1994 Number built 627 The...
SлЙfia metro station LyulinлЏЛјл╗лИлйGeneral informationLocation1324 Lyulin 7, SofiaCoordinates42┬░43Рђ▓05Рђ│N 23┬░15Рђ▓28Рђ│E / 42.71806┬░N 23.25778┬░E / 42.71806; 23.25778Owned bySofia MunicipalityOperated byMetropoliten JSCPlatformsislandTracks2Bus routes4Connections Bus lines: 42, 108, 111, N1 Tram lines: 8 ConstructionStructure typesub-surfacePlatform levels2ParkingnoBicycle facilitiesnoAccessiblean elevator to platformsArchitectK. Bochkov and B. SedmakovOther inf...

Asinan Betawi Hidangan Betawi adalah hidangan khas yang berasal dari Suku Betawi. Hidangan Betawi mudah ditemukan di acara-acara tertentu yang diselenggarakan di wilayah DKI Jakarta, Kota Depok, Kabupaten Bekasi dan Kota Bekasi (Jawa Barat) dan Kabupaten Tangerang, Kota Tangerang dan Kota Tangerang Selatan (Banten) seperti pada acara Lebaran Betawi,[1] pernikahan, hari raya Idulfitri, atau di warung-warung tertentu[2] yang menyajikan hidangan khas Betawi. Hidangan ini dipengar...
Impact of COVID-19 outbreak on environmental issues┘ѓпД┘ёпе:SHORTDESC:Impact of COVID-19 outbreak on environmental issues пфпИ┘Єп▒ пД┘ёпх┘ѕп▒ ┘Ё┘є ┘Ёп▒пхп» ┘єпДп│пД ┘ё┘ёпБп▒пХ пД┘єп«┘ЂпДпХ┘ІпД пГпДп»┘ІпД ┘Ђ┘і пД┘ёпф┘ё┘ѕпФ ┘Ђ┘і ┘ѕ┘ѕ┘ЄпД┘єпї пД┘ёпх┘і┘єпї п╣┘єп» ┘Ё┘ѓпДп▒┘єпЕ ┘Ёп│пф┘ѕ┘іпДпф пФпД┘є┘і пБ┘Ѓп│┘іп» пД┘ё┘є┘іпфп▒┘ѕпг┘і┘є ┘Ђ┘і пБ┘ѕпДпд┘ё п╣пД┘Ё 2019 (пБп╣┘ё┘Ѕ) ┘ѕпБ┘ѕпДпд┘ё 2020 (пБп│┘Ђ┘ё). [1] .[1] пгп▓пА ┘Ё┘є п│┘ёп│┘ёпЕ ┘Ё┘ѓпД┘ёпДпф пГ┘ѕ┘ёпгпДпдпГпЕ ┘Ђ┘іп▒┘ѕп│ ┘Ѓ┘ѕп▒┘ѕ┘єпД SARS-...

American brothel owner and philanthropist Eliza Haycraft (1820-1871), was a wealthy brothel madam and philanthropist, who donated money to the widows and orphans of the American Civil War. Eliza HaycraftBorn(1820-02-14)February 14, 1820DiedDecember 5, 1871(1871-12-05) (aged 51)St Louis, MissouriNationalityAmericanOccupation(s)Brothel madam and philanthropist Biography Haycraft was born on 14 February 1820. She moved to St. Louis, Missouri, from Callaway County, Missouri, in 1840, reporte...

сЂЊсЂ«УеўС║ІсЂ»ТцюУе╝тЈ»УЃйсЂфтЈѓУђЃТќЄуї«сѓётЄ║тЁИсЂїтЁесЂЈуц║сЂЋсѓїсЂдсЂёсЂфсЂёсЂІсђЂСИЇтЇЂтѕєсЂДсЂЎсђѓтЄ║тЁИсѓњУ┐йтіасЂЌсЂдУеўС║ІсЂ«С┐Ажа╝ТђДтљЉСИісЂФсЂћтЇћтіЏсЂЈсЂасЂЋсЂёсђѓ№╝ѕсЂЊсЂ«сЃєсЃ│сЃЌсЃгсЃ╝сЃѕсЂ«Сй┐сЂёТќ╣№╝ЅтЄ║тЁИТцюу┤б?: сѓ│сЃФсѓ» РђЊ сЃІсЃЦсЃ╝сѓ╣ ┬и ТЏИу▒Ї ┬и сѓ╣сѓФсЃЕсЃ╝ ┬и CiNii ┬и J-STAGE ┬и NDL ┬и dlib.jp ┬и сѓИсЃБсЃЉсЃ│сѓхсЃ╝сЃЂ ┬и TWL№╝ѕ2017т╣┤4Тюѕ№╝Ѕ сѓ│сЃФсѓ»сѓњТЅЊсЂАТіюсЂёсЂдСйюсЂБсЂЪуЊХсЂ«ТаЊ сѓ│сЃФсѓ»№╝ѕТюеТаЊсђЂ№┐й...

Ciclo empirico secondo Adriaan de Groot Con il termine ricerca empirica (dal greco ╬х╬╝¤ђ╬х╬╣¤Ђ╬╣╬▒, ovvero esperienza), in filosofia Рђћ e non solo Рђћ, s'intende un tipo di ricerca che basa le conclusioni sull'osservazione diretta o indiretta dei fatti. Lo studio di questo metodo di ricerca parte sempre da un fenomeno e si sviluppa con una analisi successiva ai fatti. L'osservazione ├е dunque la prova della realt├а: da essa il ricercatore ricava le proprie deduzioni e su di essa basa i test...

Series of microprocessors from IBM For the instruction set named Power, see Power ISA. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: IBM Power microprocessors РђЊ news ┬и newspapers ┬и books ┬и scholar ┬и JSTOR (September 2022) (Learn how and when to remove this message) POWER, PowerPC, and Power ISA architectu...

American financial services company Morgan StanleyHeadquarters at 1585 BroadwayCompany typePublicTraded asNYSE: MSS&P 100 componentS&P 500 componentIndustryFinancial servicesFounded1935; 89 years ago (1935) (the original Morgan Stanley)1924; 100 years ago (1924) (Dean Witter & Co.)1931; 93 years ago (1931) (Reynolds Securities)FounderHenry Sturgis MorganHarold StanleyDean G. WitterRichard S. Reynolds, Jr.HeadquartersMorgan...
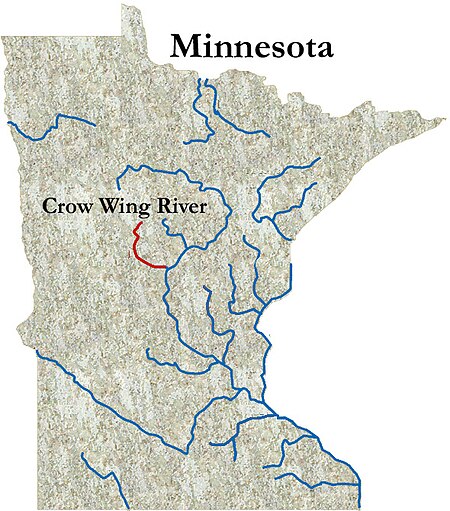
River in Minnesota, United StatesCrow Wing RiverThe Crow Wing River in Old Wadena County ParkThe Crow Wing RiverLocationCountryUnited StatesStateMinnesotaPhysical characteristicsSource • coordinates47┬░00Рђ▓07Рђ│N 94┬░44Рђ▓29Рђ│W / 47.00194┬░N 94.74139┬░W / 47.00194; -94.74139[1] • elevation1,391 ft (424 m)[1] Mouth • coordinates46┬░16Рђ▓16Рђ│N 94┬░20Рђ▓23Рђ│W / 4...

Atti dei SantiTitolo originaleActa Sanctorum Frontespizio del primo volume degli Acta Sanctorum (mese di gennaio) pubblicato nel 1643 AutoreJean Bolland 1┬ф ed. originale1643 Genereraccolta Sottogenerereligioso Lingua originalelatino Modifica dati su Wikidata ┬и Manuale Gli Acta Sanctorum (in italiano Atti dei santi) costituiscono una raccolta di documenti relativi ai santi della Chiesa avviata, nel suo nucleo primigenio, dall'erudito belga Jean Bolland (1596-1665) S.J. e poi proseguita ...

п│пф┘і┘ЂпД┘є┘і ┘Ђ┘ѕп▒┘іп│пф ┘Ёп╣┘ё┘ѕ┘ЁпДпф п┤п«пх┘іпЕ пД┘ё┘Ё┘і┘ёпДп» п│┘єпЕ 1958 (пД┘ёп╣┘Ёп▒ 65–66 п│┘єпЕ) ┘Ё┘ѕпДпи┘єпЕ пД┘ё┘ѕ┘ёпД┘іпДпф пД┘ё┘ЁпфпГп»пЕ пД┘ёпГ┘іпДпЕ пД┘ёп╣┘Ё┘ё┘іпЕ пД┘ё┘Ёп»п▒п│пЕ пД┘ёпБ┘Ё пгпД┘Ёп╣пЕ ┘Ё┘іп┤┘іп║пД┘є ┘Ёп┤п▒┘Ђ пД┘ёп»┘Ѓпф┘ѕп▒пД┘Є пг┘ѕ┘є ┘Є┘єп▒┘і ┘Є┘ѕ┘ёпД┘єп» пД┘ё┘Ё┘Є┘єпЕ п╣┘јпД┘ё┘љ┘Ё┘јпЕ пГпДп│┘ѕпе ┘ЁпгпД┘ё пД┘ёп╣┘Ё┘ё п«┘ѕпДп▒п▓┘Ё┘іпДпф ┘ѕп▒пДпФ┘іпЕ ┘Ё┘ѕпИ┘ЂпЕ ┘Ђ┘і пгпД┘Ёп╣пЕ ┘є┘і┘ѕ┘Ё┘Ѓп│┘і┘Ѓ┘ѕпї ┘ѕ┘Ёпцп│п│пЕ п│пД┘є№┐й...

Buddhist mummification It has been suggested that this article be merged into Buddhist mummy. (Discuss) Proposed since July 2024. The body of the Thai Buddhist monk Luang Pho Daeng at Wat Khunaram, Ko Samui, Thailand Sokushinbutsu (тЇ│У║ФС╗Ј) are a type of Buddhist mummy. In Japan the term refers to the practice of Buddhist monks observing asceticism to the point of death and entering mummification while alive.[1][2] Although mummified monks are seen in a number of Buddhist co...

MokpoвфЕьЈгВІю Ciudad Bandera MokpoLocalizaci├│n de Mokpo en Corea del Sur Coordenadas 34┬░47Рђ▓37Рђ│N 126┬░23Рђ▓19Рђ│E / 34.793611111111, 126.38861111111Idioma oficial CoreanoEntidad Ciudad Рђб Pa├Гs Corea del SurSuperficie Рђб Total 50 km┬▓Altitud Рђб Media 2 m s. n. m.Poblaci├│n (2011) Рђб Total 245 446 hab. Рђб Densidad 5200 hab./km┬▓Huso horario UTC + 9Hermanada con Xiamen Beppu Sitio web oficial [edi...

Let's TalkAlbum mini karya HomogenicDirilis6 Juni 2012Direkam2012GenreSynth-popDurasi25:48LabelUNKL347Kronologi Homogenic Let a Thousand Flowers Bloom(2010)Let a Thousand Flowers Bloom2010 Let's Talk(2012) HMGNC(2017)HMGNC2017 Singel dalam album Let's Talk Get Up and GoDirilis: 2012 Takkan Berhenti di SiniDirilis: 2012 Let's Talk adalah album mini oleh grup musik electropop Indonesia Homogenic, dirilis pada tanggal 6 Juni 2012. Ini adalah album terakhir band untuk menggunakan nama Hom...

Pour les articles homonymes, voir San Remo. Cet article est une ├Еbauche concernant lРђЎhistoire, la diplomatie et la Ligurie. Vous pouvez partager vos connaissances en lРђЎam├Еliorant (comment ?) selon les recommandations des projets correspondants. Les d├Еl├Еgu├Еs ├а la conf├Еrence. Proc├еs-verbal de la conf├Еrence de San Remo. La conf├Еrence de San Remo est une conf├Еrence internationale qui a eu lieu du 19 au 26 avril 1920 dans le ch├бteau Devachan ├а Sanremo (selon la graphie actue...

For the metropolitan area, see Springfield metropolitan area, Massachusetts. City in Massachusetts, United StatesSpringfield, MassachusettsCitySpringfield skylineSymphony HallThe Puritan statue of pioneer Samuel ChapinCourt Square Historic DistrictBasketball Hall of FameHampden County Memorial Bridge overlooking the Connecticut RiverSpringfield Armory National Historic Site FlagSealCoat of armsNickname(s): The City of Firsts; The City of Progress;[1][2][3] The Cit...


