תנועת בוגרים
| ||||||||||
Read other articles:
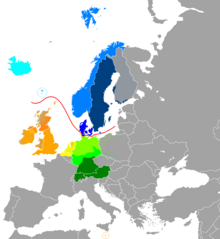
West Germanic language EnglishPronunciation/ˈɪŋɡlɪʃ/[1]Native toUnited Kingdom, Anglo-America, Australia, Ireland, New Zealand and other locations in the English-speaking worldSpeakersL1: 380 million (2021)[2]L2: 1.077 billion (2021)[3]Total: 1.457 billionLanguage familyIndo-European GermanicWest GermanicNorth Sea GermanicAnglo-FrisianAnglicEnglishEarly formsProto-Indo-European Proto-Germanic Old English Middle English Early Modern English Writing syste...

Gedung Sūmitsu-in pada tahun 1922. Dewan Penasihat Jepang (枢密院code: ja is deprecated , Sūmitsu-in) adalah sebuah dewan penasehat untuk Kaisar Jepang yang berfungsi antara 1888-1947. Bentuk dewan ini sebagian menirukan Dewan Penasihat Britania Raya, yang memberikan saran kepada Tahta Kekaisaran mengenai permasalahan yang sangat penting, antara lain termasuk: (1) mengusulkan amendemen terhadap Undang-Undang Rumah Tangga Kekaisaran 1889 dan Konstitusi Kekaisaran Jepang; (2) masalah-masal...

Hikaru Naomoto Hikaru Naomoto saat FC Bayern (wanita) vs SC Freiburg (wanita), Mei 2019Informasi pribadiNama lengkap Hikaru NaomotoTanggal lahir 3 Maret 1994 (umur 30)Tempat lahir Prefektur Fukuoka, JepangPosisi bermain GelandangKarier senior*Tahun Tim Tampil (Gol)2007–2011 Fukuoka J. Anclas 26 (0)2012– Urawa Reds 102 (9)Tim nasional2014– Jepang 15 (0) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Hikaru Naomoto (猶本 光, lahir 3 Maret 1994) adalah seora...

Museum PedirPendiri Pedir Museum, Masykur Syarifuddin ketika menerima kunjungan tim dari Kementerian Pendidikan dan Kebudayaan Pedir Museum adalah sebuah museum yang terletak di Blang Glong, Pidie Jaya dan memiliki cabang di Punge Blang Cut, Banda Aceh . Museum ini didirikan oleh Masykur Syarifuddin pada tanggal 6 Juni 2015. Museum ini mengkoleksi berbagai benda-benda kuno peninggalan peradaban di Aceh seperti manuskrip, mata uang, senjata, keramik dan berbagai artefak lainnya. Saat ini Pedir...

le Fium'AltoFiumaltu Le Fium'Alto vu depuis le pont d'Acitaja à Folelli. Cours du Fium'Alto. Caractéristiques Longueur 30,9 km [1] Bassin 127 km2 [1] Bassin collecteur Fium'Alto Débit moyen 1,36 m3/s (Taglio-Isolaccio) [2] Nombre de Strahler 5 Organisme gestionnaire Comité de bassin de Corse[3] Régime pluvial méridional Cours Source 1 km au sud du Monte San Petrone (1767 m) · Localisation Pie-d'Orezza · Altitude 1 469 m · Coordonnées 42° 23′ 06...

L'imperatore Teodosio I offre una corona d'alloro al vincitore di una gara circense (obelisco di Teodosio nell'Ippodromo di Costantinopoli). La corona d'alloro (in latino laurea insignis), che nella mitologia greco-romana simboleggiava la sapienza e la gloria, cingeva la fronte dei vincitori di celebrazione atletiche (come i Giochi pitici o Delfici) ed era simbolo distintivo dei massimo dotti e poeti, detti laureati al cingere della stessa. L’Alloro era considerato una pianta sacra nella cu...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

1954 SF novel by Robert A. Heinlein This article is about the 1954 science fiction novel. For other uses, see Star Beast (disambiguation). The Star Beast First edition cover for The Star BeastAuthorRobert A. HeinleinCover artistClifford GearyCountryUnited StatesLanguageEnglishSeriesHeinlein juvenilesGenreScience fictionPublisherScribner'sPublication date1954Media typePrint (hardback and paperback)Preceded byStarman Jones Followed byTunnel in the Sky The Star Bea...
Королівські військово-повітряні сили Нової Зеландії Прапор Дата створення / заснування 1923 Участь у військовому конфлікті Друга світова війна і Східний Тимор Текст девізу Te Tauaarangi o Aotearoa Країна Нова Зеландія Місце розташування Веллінгтон Роботи в колекції Авст�...

Pattern that has no predecessors A Garden of Eden in Conway's Game of Life, discovered by R. Banks in 1971.[1] The cells outside the image are all dead (white). An orphan in Life found by Achim Flammenkamp. Black squares are required live cells; blue x's are required dead cells. In a cellular automaton, a Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configuratio...

Political system of South Korea This article is about the politics of the Republic of Korea. For other uses, see Politics of Korea (disambiguation). For the article about the politics of the Democratic People's Republic of Korea, see Politics of North Korea. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Politics of South Korea – ...

2010 British TV series or programme Miliband of BrothersWritten byDavid QuantickStarringHenry Lloyd-HughesBen Lloyd-HughesCountry of originUnited KingdomOriginal languageEnglishOriginal releaseRelease2010 (2010) Miliband of Brothers is a 2010 satirical docu-drama following the lives and careers of British politicians David Miliband and younger brother Ed, who at the time were both contesting the 2010 Labour leadership contest. Written by David Quantick, the programme was first shown on ...

Overview of racism in Portugal Racism in Portugal has a long history, including the early modern persecution of Muslims and Jews and Portugal's involvement in the trade in enslaved people from West Africa. Today in Portugal, the number of attacks against Afro-Portuguese people and Romani people from one year to the next is uneven and those attacks are always promptly reported on the media and investigated by the police.[1] Those two groups of people have also had a disproportionate re...

Yui KoikeLahir4 April 1991 (umur 33)[1] Prefektur Saitama, JepangSukuOrang JepangTinggi156 m (511 ft 9+1⁄2 in)Warna rambutHitamWarna mataHitamPengukuran78-61-83 cm31-24-33 in Yui Koike (小池 唯code: ja is deprecated , Koike Yui, lahir 4 April 1991) adalah aktris dan gravure idol asal Jepang. Ia mulai berkarier di dunia artis sejak tahun 2006, & ia dikenal dengan peran-perannya dalam serial tokusatsu & drama: sebagai Ahim de Famille / Gokai Pink dal...

Эта статья — об археологическом памятнике. О современном городе см. Аннау; о мечети см. Дом красоты. Анаутуркм. Änew Закаспийская область. Развалины персидской крепости в Анау. С фотографии, гравёр М. Рашевский. «Нива», №10, 1888 37°53′52″ с. ш. 58°31′43″ в...

Legislative branch of the state government of North Carolina For the building, see North Carolina State Legislative Building. North Carolina General AssemblySeal of the North Carolina General AssemblyTypeTypeBicameral HousesSenateHouse of RepresentativesHistoryFoundedMay 20, 1775(249 years ago) (1775-05-20)LeadershipPresident of the Senate &Lieutenant GovernorMark Robinson (R) since January 9, 2021 President pro tempore of the SenatePhil Berger (R) since January 26, 2011...

Pour les articles homonymes, voir Cullberg. Johan CullbergBiographieNaissance 6 janvier 1934Paroisse de la cathédrale d’Uppsala (d) (Suède)Décès 14 juin 2022 (à 88 ans)Högalids distrikt (d) (Stockholm, Suède)Nationalité suédoiseActivités Psychiatre, psychologuePère John Cullberg (en)Fratrie Erland Cullberg (en)Staffan Cullberg (d)Conjoints Asta Bolin (d) (de 1961 à 1968)Marta Cullberg Weston (d) (à partir de 1971)Inger Alfvén (en) (de 1993 à 2022)Autres informationsDist...

Masjid Raya Baiturrahman SemarangMenara Masjid Baiturrahman SemarangAgamaAfiliasiIslamLokasiLokasiSemarang, IndonesiaArsitekturTipeMasjidPeletakan batu pertama1968Rampung1974Kapasitas-+10000 jamaah Masjid Raya Baiturrahman Semarang (Hanacaraka: ꦩꦱ꧀ꦗꦶꦢ꧀ꦫꦪꦧꦻꦠꦸꦂꦫꦃꦩꦤ꧀ꦱꦼꦩꦫꦁ) merupakan sebuah masjid yang terletak di Semarang, Indonesia. Masjid ini dibangun pada tahun 1968 dan selesai pada tahun 1974. Pembangunan Masjid Raya Baiturahman dimulai pada 10...
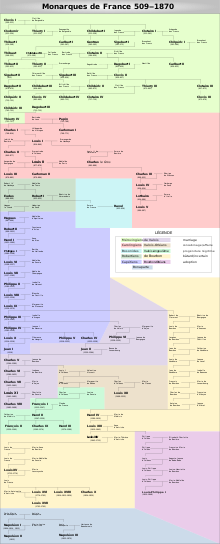
This article is about French kings beginning with the 843 Treaty of Verdun. For kings before 843, see List of Frankish kings. From top; left to right: Robert I, Hugh Capet, Louis IX, Francis I, Henry IV, Louis XIV, Louis XVI, Napoleon I, Napoleon III The family tree of Frankish and French monarchs (509–1870)France was ruled by monarchs from the establishment of the Kingdom of West Francia in 843 until the end of the Second French Empire in 1870, with several interruptions. Classical French...

الحل الهندسي للمتطابقة الهامة ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 {\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\,} في الرياضيات، يطلق اسم المتطابقات الهامة[1] أو المتطابقات الشهيرة أو المتساويات الهامة على بعض المتساويات التي تطبق على أعداد أو حدوديات. و هي تساعد على تسريع عمليات الحساب، تبسيط بعض...
