ЧӘЧҗЧ•ЧЁЧҷЧҷЧӘ Ч”Ч”ЧӘЧ Ч’Ч©Ч•ЧҷЧ•ЧӘ Ч”ЧһЧ•ЧңЧ§Ч•ЧңЧЁЧҷЧ•ЧӘ
|
Read other articles:

Щ…ЩҸШӯЩ…ЩҺЩ‘ШҜ Ш§Щ„ШЈЩҲЩҺЩ‘Щ„ (ШЁШ§Щ„ШӘШұЩғЩҠШ© Ш§Щ„Ш№Ш«Щ…Ш§ЩҶЩҠШ©: Щ…ЩҸШӯЩ…ЩҺЩ‘ШҜ Ш§ЩҲЩҺЩ‘Щ„)вҖҸ Ш§Щ„ШӯЩғЩ… Щ…ШҜШ© Ш§Щ„ШӯЩғЩ… 816 - 824ЩҮЩҖ\1413 - 1421Щ… Ш№ЩҮШҜ ЩӮЩҠШ§Щ… Ш§Щ„ШҜЩҲЩ„Ш© Ш§Щ„Ш№Ш«Щ…Ш§ЩҶЩҠШ© Ш§Щ„Щ„ЩӮШЁ ЪҶЩ„ШЁЩҠШҢ ЩғШұШҙШ¬ЩҠШҢ Щ…ЩҸЩ…ЩҮЩҗЩ‘ШҜ Ш§Щ„ШҜЩҲЩ„Ш© ЩҲШ§Щ„ШҜЩҠЩҶШҢ ШәЩҠЩҺЩ‘Ш§Ш« Ш§Щ„ШҜЩҠЩҶШҢ Ш§Щ„Щ…Щ„Щғ Ш§Щ„Ш№Ш§ШҜЩ„ Ш§Щ„ШӘШӘЩҲЩҠШ¬ 816ЩҮЩҖ\1413Щ… Ш§Щ„Ш№Ш§ШҰЩ„Ш© Ш§Щ„ШӯШ§ЩғЩ…Ш© ШўЩ„ Ш№Ш«Щ…Ш§ЩҶ Ш§Щ„ШіЩ„Ш§Щ„Ш© Ш§Щ„Щ…Щ„ЩғЩҠШ© Ш§Щ„Ш№Ш«Щ…Ш§ЩҶЩҠШ© ЩҶЩҲШ№ Ш§Щ„Ш®Щ„Ш§ЩҒШ© ЩҲШұШ§Ш«ЩҠШ©...

Gambling in the U.S. state of Texas Legal forms of gambling in the U.S. state of Texas include the Texas Lottery; parimutuel wagering on horse and greyhound racing; limited charitable bingo, limited charitable raffles, and three Native American casinos. Other forms of gambling are illegal in Texas.[1] Texas Sports Betting Legislation Status Bills to legalize sports betting legislation in Texas have not received favorable attention. Sports bettingвҖ”whether via bricks and mortar or onl...
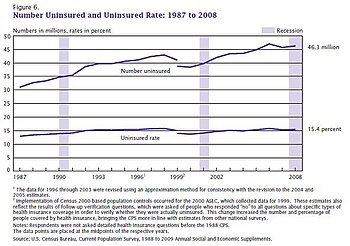
Healthcare in the United States Government health programs Federal Employees Health Benefits Program (FEHBP) Indian Health Service (IHS) Medicaid / State Health Insurance Assistance Program (SHIP) Medicare Prescription Assistance (SPAP) Military Health System (MHS) / Tricare Children's Health Insurance Program (CHIP) Program of All-Inclusive Care for the Elderly (PACE) Veterans Health Administration (VHA) Private health coverage Consumer-driven healthcare Flexible spending account (FSA) Heal...

Charity Shield FA 1908TurnamenCharity Shield FA Manchester United Queens Park Rangers Final Manchester United Queens Park Rangers 1 1 Tanggal27 April 1908StadionStamford Bridge, LondonPenonton6.000Ulangan Queens Park Rangers Manchester United 4 0 Tanggal29 Agustus 1908StadionStamford Bridge, LondonPenonton50.0001909 → Charity Shield FA 1908 adalah pertandingan sepak bola antara Manchester United dan Queens Park Rangers yang diselenggarakan pada 27 April 1908 di Stamford Bridge, London. ...

Voce principale: Vicenza Calcio. A.C. Lanerossi VicenzaStagione 1965-1966Sport calcio SquadraVicenza Calcio Allenatore Aldo Campatelli Presidente Delio Giacometti Serie A6Вә posto Coppa ItaliaQuarti di finale Maggiori presenzeCampionato: LuГӯs VinГӯcio (34) Miglior marcatoreCampionato: LuГӯs VinГӯcio (25)Totale: LuГӯs VinГӯcio (28) StadioRomeo Menti 1964-1965 1966-1967 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Associazione Calcio Lanerossi Vic...

Halaman ini berisi artikel tentang film. Untuk buku, lihat The Silent World: A Story of Undersea Discovery and Adventure. The Silent WorldPoster film pertamaSutradaraJacques-Yves CousteauLouis MalleDitulis olehJacques-Yves Cousteau, James DuganPerusahaanproduksiFSJYC ProductionRequins AssociГ©sSociГ©tГ© FilmadTitanusDistributorRank Organisation (Prancis)Columbia Pictures (Amerika Serikat)Tanggal rilis26 Mei 1956 (1956-05-26) (Cannes)15 Agustus 1956 (1956-08-15) (Jepang)24 September ...

жӯӨжўқзӣ®еҸҜеҸӮз…§иӢұиӘһз¶ӯеҹәзҷҫ科зӣёжҮүжўқзӣ®жқҘжү©е……гҖӮ (2021е№ҙ5жңҲ6ж—Ҙ)иӢҘжӮЁзҶҹжӮүжқҘжәҗиҜӯиЁҖе’Ңдё»йўҳпјҢиҜ·еҚҸеҠ©еҸӮиҖғеӨ–иҜӯз»ҙеҹәзҷҫ科жү©е……жқЎзӣ®гҖӮиҜ·еӢҝзӣҙжҺҘжҸҗдәӨжңәжў°зҝ»иҜ‘пјҢд№ҹдёҚиҰҒзҝ»иҜ‘дёҚеҸҜйқ гҖҒдҪҺе“ҒиҙЁеҶ…е®№гҖӮдҫқзүҲжқғеҚҸи®®пјҢиҜ‘ж–ҮйңҖеңЁзј–иҫ‘ж‘ҳиҰҒжіЁжҳҺжқҘжәҗпјҢжҲ–дәҺи®Ёи®әйЎөйЎ¶йғЁж Үи®°{{Translated page}}ж ҮзӯҫгҖӮ зәҰзҝ°ж–ҜйЎҝзҺҜзӨҒKalama Atoll зҫҺеңӢжң¬еңҹеӨ–е°Ҹеі¶е¶ј Johnston Atoll ж——е№ҹйўӮжӯҢпјҡгҖҠжҳҹжўқж——гҖӢThe Star-Spangled Bannerзҙ„зҝ°ж–Ҝй “з’°зӨҒпҝҪ...

Р”РөСҖжавРҪРёР№ РәРҫРјС–СӮРөСӮ СӮРөР»РөРұР°СҮРөРҪРҪСҸ С– СҖР°РҙС–РҫРјРҫРІР»РөРҪРҪСҸ РЈРәСҖаїРҪРё (Р”РөСҖР¶РәРҫРјСӮРөР»РөСҖР°РҙС–Рҫ) РҹСҖРёРјС–СүРөРҪРҪСҸ РәРҫРјС–СӮРөСӮСғЗагалСҢРҪР° С–РҪС„РҫСҖРјР°СҶС–СҸРҡСҖаїРҪР° РЈРәСҖаїРҪаДаСӮР° СҒСӮРІРҫСҖРөРҪРҪСҸ 2003РҡРөСҖС–РІРҪРө РІС–РҙРҫРјСҒСӮРІРҫ РҡР°РұС–РҪРөСӮ РңС–РҪС–СҒСӮСҖС–РІ РЈРәСҖаїРҪРёР С–СҮРҪРёР№ РұСҺРҙР¶РөСӮ 1 964 898 500 вӮҙ[1]Р“РҫР»РҫРІР° РһР»РөРі РқаливайРәРҫРҹС–РҙРІС–РҙРҫРјСҮС– РҫСҖ...

Village and civil parish in North Yorkshire, England Human settlement in EnglandEggboroughHorse and Jockey pub in the village, with power station chimney visible in backgroundEggboroughLocation within North YorkshirePopulation1,952 (2011 Census)[1]OS grid referenceSE565235Civil parishEggboroughUnitary authorityNorth YorkshireCeremonial countyNorth YorkshireRegionYorkshire and the HumberCountryEnglandSovereign stateUnited KingdomPost townGOOLEPostcode ...

Association football club in Bulgaria Football clubFC Vitosha BistritsaFull nameFootball Club Vitosha BistritsaNickname(s)The Bistritsa TigersShort nameVitoshaFounded1958; 66 years ago (1958)GroundStadion BistritsaCapacity2,500ManagerNikolay HristozovLeagueSouthwest Third League2022вҖ“23Second League, 17th (relegated)WebsiteClub website Home colours Away colours Third colours FC Vitosha (Bulgarian: РӨРҡ Р’РёСӮРҫСҲР°) is a Bulgarian association football club based in Bistrits...

City in Fars province, Iran For the administrative division of Fars province, see Kharameh County. For other places with similar names, see Karamah and Karameh. City in Fars, IranKharameh Persian: Ш®ШұШ§Щ…ЩҮCityKharamehCoordinates: 29В°29вҖІ57вҖіN 53В°18вҖІ47вҖіE / 29.49917В°N 53.31306В°E / 29.49917; 53.31306[1]CountryIranProvinceFarsCountyKharamehDistrictCentralPopulation (2016)[2] вҖў Total18,477Time zoneUTC+3:30 (IRST) Kharameh (Persia...

Satya Titiek Atyani DjoedirSatya Titiek sebagai Wakil Bupati Barito Selatan Periode Pertama (2011вҖ“2016) Wakil Bupati Barito Selatan ke-2Masa jabatan22 Mei 2017 вҖ“ 22 Mei 2022BupatiEddy Raya SamsuriMasa jabatan18 September 2011 вҖ“ 18 September 2016BupatiFarid YusranPendahuluIrawansyahPenggantiPetahana Informasi pribadiLahir18 September 1956 (umur 67)SurabayaKebangsaanIndonesiaPartai politikPartai NasDemProfesiPolitisiSunting kotak info вҖў L вҖў B Satya...

Questa voce o sezione sugli argomenti sceneggiatori francesi e attori francesi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce sugli argomenti sceneggiatori francesi e attori francesi ГЁ solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti ...

Щ„Щ…Ш№Ш§ЩҶЩҚ ШЈШ®ШұЩүШҢ Ш·Ш§Щ„Ш№ Ш№Ш¬Ш§ШҰШЁ Ш§Щ„ШҜЩҶЩҠШ§ (ШӘЩҲШ¶ЩҠШӯ). Ш№Ш¬Ш§ШҰШЁ Ш§Щ„ШҜЩҶЩҠШ§ Ш§Щ„ШіШЁШ№ Ш§Щ„ЩӮШҜЩҠЩ…Ш© Ш№Щ„Щү Щ…ШҜЩү Ш§Щ„Ш№ШөЩҲШұ ШӘЩ… Ш¬Щ…Ш№ ЩӮЩҲШ§ШҰЩ… Щ…Ш®ШӘЩ„ЩҒШ© Щ…ЩҶ Ш№Ш¬Ш§ШҰШЁ Ш§Щ„ШҜЩҶЩҠШ§ Щ„ЩҒЩҮШұШіШ© ШЈЩғШ«Шұ Ш§Щ„ШЈШҙЩҠШ§ШЎ Ш§Щ„Ш№Ш¬ЩҠШЁШ© Ш§Щ„ШӘЩҠ Щ…ЩҶ ШөЩҶШ№ Ш§Щ„ШҘЩҶШіШ§ЩҶ ЩҲШӘЩ„Щғ Ш§Щ„Ш·ШЁЩҠШ№ЩҠШ© ЩҒЩҠ Ш§Щ„Ш№Ш§Щ„Щ…. ШҘЩҶ Ш№Ш¬Ш§ШҰШЁ Ш§Щ„ШҜЩҶЩҠШ§ Ш§Щ„ШіШЁШ№ Ш§Щ„ЩӮШҜЩҠЩ…Ш© ЩҮЩҠ ШЈЩҲЩ„ ЩӮШ§ШҰЩ…Ш© Щ„ШЈЩҮЩ… Ш§Щ„ШҘШЁШҜШ§Ш№Ш§ШӘ Ш§Щ„ШӘЩҠ ШөЩҶШ№ЩҮШ§ Ш§Щ„ШҘЩҶШіШ§пҝҪ...

Chino XL (2012) Chino XL (* 8. April 1974 in der Bronx, New York City; bГјrgerlich Derek Barbosa; вҖ 28. Juli 2024) war ein US-amerikanischer Rapper und Schauspieler. Er war bekannt fГјr seine Battle-Rap-FГӨhigkeiten und durch eine Auseinandersetzung (East Coast vs. West Coast) mit 2Pac. Inhaltsverzeichnis 1 Karriere 2 Diskographie 3 Weblinks 4 Einzelnachweise Karriere Derek Barbosa wuchs in East Orange, New Jersey auf. Nach der Entstehung der Gruppe Art of Origin wurde Chino XL im Alter von...

BLOC1S6 Щ…Ш№ШұЩҒШ§ШӘ ШЈШіЩ…Ш§ШЎ ШЁШҜЩҠЩ„Ш© BLOC1S6, BLOS6, HPS9, PA, PALLID, PLDN, biogenesis of lysosomal organelles complex 1 subunit 6 Щ…Ш№ШұЩҒШ§ШӘ Ш®Ш§ШұШ¬ЩҠШ© Ш§Щ„ЩҲШұШ§Ш«Ш© Ш§Щ„Щ…ЩҶШҜЩ„ЩҠШ© Ш§Щ„ШЁШҙШұЩҠШ© Ш№ШЁШұ Ш§Щ„ШҘЩҶШӘШұЩҶШӘ 604310 MGI: MGI:1927580 HomoloGene: 40841 GeneCards: 26258 Ш№Щ„Щ… Ш§Щ„ЩҲШ¬ЩҲШҜ Ш§Щ„Ш¬ЩҠЩҶЩҠ ЩҲШёШ§ШҰЩҒ Ш¬ШІЩҠШҰЩҠШ© вҖў protein homodimerization activityвҖў actin filament bindingвҖў вҖҸGO:0001948ШҢ вҖҸGO:0016582 ШұШЁШ· ШЁШұЩҲШӘЩҠЩҶЩҠвҖў identical protein bindi...

Legendary 1st Emperor of Japan (r. 660вҖ“585 BC) You can help expand this article with text translated from the corresponding article in Japanese. Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Consider adding a top...

Marxist term to describe a subsection of the underclass Part of a series onMarxism Theoretical works Economic and Philosophic Manuscripts of 1844 The Condition of the Working Class in England The German Ideology The Communist Manifesto The Eighteenth Brumaire of Louis Bonaparte Grundrisse Capital Critique of the Gotha Programme Dialectics of Nature The Origin of the Family, Private Property and the State What Is to Be Done? The Accumulation of Capital Philosophical Notebooks Terrorism and Com...
Symbol used to represent a monetary currency's name For the symbol representing a generic currency, see Currency sign (generic). For three-letter currency codes, see ISO 4217. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Currency symbol вҖ“ news В· newspapers В· books В· scholar В· JSTOR (November 2021) (Learn ...

Vous lisez un В« bon article В» labellisГ© en 2010. Ferrari S.p.A. Le Cavallino Rampante, logo de Ferrari. SiГЁge social et usine de Ferrari Г Maranello en Italie. CrГ©ation 1947 Dates clГ©s 1969 : Fiat entre dans le capital 1988 : mort d'Enzo Ferrari 1991 : Luca di Montezemolo prend la prГ©sidence 1997 : Rachat de Maserati 2015 : scission avec le groupe Fiat Chrysler Automobiles Fondateurs Enzo Ferrari Forme juridique SociГ©tГ© par actions de droit italie...









![{\displaystyle N_{A}\sigma _{AB}{\sqrt {\frac {8k_{B}T}{\pi \mu _{AB}}}}[A][B]=N_{A}r_{AB}^{2}{\sqrt {\frac {8\pi k_{B}T}{\mu _{AB}}}}[A][B]=Z[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a26619250e88af338e64a8f47d0f7335ba9ac44)

![{\displaystyle r=Z\rho [A][B]\exp \left({\frac {-E_{a}}{RT}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec84d554ab59174b9f67993aa0e2b7678043d4f)
![{\displaystyle \scriptstyle r=k(T)[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/331fdb6f0fd9b316c138f0dbdd321f7a47fb709e)

