שושלת סונג
| |||||||||||||||||||||||||||||||||||
Read other articles:

Uomo Ragno 2099Uomo Ragno 2099, disegnato da Rick Leonardi UniversoMarvel 2099 Nome orig.Spider-Man 2099 Lingua orig.Inglese AutoriPeter David Rick Leonardi EditoreMarvel Comics - Marvel 2099 1ª app.Agosto 1992 1ª app. inAmazing Spider-Man (vol. 1[1]) n. 365 Editore it.Star Comics - Marvel Italia 1ª app. it.Aprile 1993 1ª app. it. inMarvel 2099 Speciale n. 0 Voci orig.Dan Gilvezan (Spider-Man: Shattered Dimensions) Yuri Lowenthal (Marvel Super Hero Squad...

judul halaman Buku Philosophiæ Naturalis Principia Mathematica, yang berarti dalam bahasa Latin Prinsip Matematika dari Filsafat Alam adalah sebuah buku karya Isaac Newton. Buku ini diterbitkan pada 5 Juli 1687.[1][2] Dalam buku ini, Newton menyatakan ketiga hukum gerakannya yang membentuk dasar mekanika klasik, serta hukum gravitasi universal, dan penurunan hukum Kepler yang sebelumnya diperoleh secara empiris. Dalam merumuskan teori-teori fisikanya, Newton mengembangkan cab...

ضريح حافظ الشيرازيحافظیه (بالفارسية) المقصورة التي تظلل الضريحمعلومات عامةنوع المبنى ضريحالمكان شيراز، إيرانالمنطقة الإدارية مقاطعة شيراز[1] البلد إيرانالتصميم والإنشاءالنمط المعماري عمارة بهلوية المهندس المعماري الفرنسي أندريه غودارمعلومات أخرىالإحداثيات 29°37′3...

Penaklukan Yunnan oleh MingBagian dari penaklukan militer Dinasti MingPenaklukan Yunan oleh Ming 1381―1382Tanggal1381–1382LokasiYunnanHasil Kemenangan Ming[1]Pihak terlibat Dinasti Ming Sisa-sisa Yuan di YunnanWangsa DuanTokoh dan pemimpin Kaisar HongwuFu YoudeLan YuMu Ying BasalawarmiDuan GongKekuatan 250.000[2] dan Muslim loyalis Ming Ribuan tentara Mongol dan Muslim loyalis YuanKorban Ribuan tewas, ratusan dikebiri Penaklukan Yunnan oleh Ming adalah tahap terakhir dalam...

For related races, see 1928 United States gubernatorial elections. 1928 Delaware gubernatorial election ← 1924 November 6, 1928 1932 → Nominee C. Douglass Buck Charles M. Wharton Party Republican Democratic Popular vote 62,683 40,824 Percentage 60.56% 39.44% Governor before election Robert P. Robinson Republican Elected Governor C. Douglass Buck Republican Elections in Delaware Federal government Presidential elections 1788-89 1792 1796 1800 1804 1808 1812 1...

لما يُشار إليه أحيانًا بالجمهورية الفدرالية الاشتراكيه الروسية داخل الاتحاد السوفيتي والتي تعرف باسم روسيا السوفيتية، طالع جمهورية روسيا السوفيتية الاشتراكية. الاتحاد السوفيتي اتحاد الجمهوريات الاشتراكية السوفيتية Союз Советских Социалистических РеспубликSoyuz ...

Gambar halaman pertama Beowulf, sebuah teks dalam bahasa Inggris Kuno. Sejarah bahasa Inggris bermula dari migrasi Anglo-Saxon ke pulau Britania pada sekitar 1.500 tahun yang lalu. Bahasa Inggris adalah sebuah bahasa Jermanik Barat yang berasal dari dialek-dialek Anglo-Frisia yang dibawa ke pulau Britania oleh para imigran Jermanik dari beberapa bagian barat laut daerah yang sekarang disebut Belanda dan Jerman. Pada awalnya, bahasa Inggris Kuno adalah sekelompok dialek yang mencerminkan asal ...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

NATO strategic-level military command SACT redirects here. For the educational institution in Kerala, see St. Aloysius College, Thrissur. Allied Command TransformationEmblemFounded19 June 2003Part ofNorth Atlantic Treaty Organization (NATO)HeadquartersNaval Support Activity Hampton RoadsNorfolk, Virginia (USA)Websitewww.act.nato.intCommandersCurrentcommanderGénéral Philippe Lavigne, French Air and Space ForceMilitary unit Allied Command Transformation (ACT) (French: Commandement allié...

Marvel Comics character This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article...

Leigné-les-BoiscomuneLeigné-les-Bois – Veduta LocalizzazioneStato Francia Regione Nuova Aquitania Dipartimento Vienne ArrondissementChâtellerault CantoneChâtellerault-3 TerritorioCoordinate46°45′N 0°42′E / 46.75°N 0.7°E46.75; 0.7 (Leigné-les-Bois)Coordinate: 46°45′N 0°42′E / 46.75°N 0.7°E46.75; 0.7 (Leigné-les-Bois) Superficie29,41 km² Abitanti597[1] (2009) Densità20,3 ab./km² Altre informazioniCod. post...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Diano d'Albacomune Diano d'Alba – VedutaScorcio su Diano d'Alba dal punto panoramico LocalizzazioneStato Italia Regione Piemonte Provincia Cuneo AmministrazioneSindacoEzio Cardinale TerritorioCoordinate44°39′N 8°02′E / 44.65°N 8.033333°E44.65; 8.033333 (Diano d'Alba)Coordinate: 44°39′N 8°02′E / 44.65°N 8.033333°E44.65; 8.033333 (Diano d'Alba) Altitudine496 m s.l.m. Superficie17,54 km² Abitanti3 576[1]...
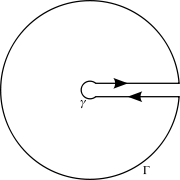
Method of evaluating certain integrals along paths in the complex plane This article is about the line integral in the complex plane. For the general line integral, see Line integral. Part of a series of articles aboutCalculus ∫ a b f ′ ( t ) d t = f ( b ) − f ( a ) {\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)} Fundamental theorem Limits Continuity Rolle's theorem Mean value theorem Inverse function theorem Differential Definitions Derivative (generalizations) Dif...

Elections to the Court of Common Council of the City of London Corporation on 22 March 2017 2017 City of London Corporation election ← 2013 23 March 2017 2022 → 100 seats to the Court of Common Council51 seats needed for a majority First party Second party Third party Party Independent Temple & Farringdon Together Labour Last election 100 seats, 96%[1] Did not stand 0 seats, 4% Seats before 99 0 1 Seats won 85 10 5 Seat chang...

1995 single by UsherThe Many WaysSingle by Usherfrom the album Usher ReleasedJanuary 26, 1995Length5:43 (album version)4:34 (radio edit)Label LaFace Arista Songwriter(s) Dave Hall Albert Brown Producer(s)Dave Jam HallUsher singles chronology Think of You (1994) The Many Ways (1995) You Make Me Wanna... (1997) The Many Ways is a song by American singer Usher. It was written and produced by Dave Hall and Al B. Sure! for his self-titled debut album (1994), while production was helmed by Hall. Re...

Pour les articles homonymes, voir 243e régiment. 243e régiment d'artillerie Cendrier commémoratif aux armes du 243e RAC Création 1917 Dissolution 1940 Pays France Branche Armée de terre Type Régiment d'artillerie Rôle Artillerie divisionnaire Ancienne dénomination AD53, ACD53 Surnom ACD37, 243e RALD Équipement 36 pièces de 75 (1917)12 pièces de 155C Schneider (1920) Guerres Première Guerre mondialeSeconde Guerre mondiale modifier Le 243e régiment d'artillerie est un r...

FIFA Ballon d'or 2011 Lionel Messi.Généralités Sport Football Organisateur(s) FIFA et France Football Éditions 56e Catégorie Trophée mondial Date 2011 Participants 23 joueurs nommés Palmarès Vainqueur Lionel Messi (3) Deuxième Cristiano Ronaldo Troisième Xavi Navigation Édition précédente Édition suivante modifier Le FIFA Ballon d'or 2011 est un trophée récompensant le meilleur footballeur du monde au cours de l'année civile 2011. La 56e remise du trophée du Ballon d'o...

Phyllis SecklerSoror MeralTitleGuiding TeacherPersonalBornPhyllis Evalina Pratt(1917-06-18)18 June 1917Edmonton, Alberta, CanadaDied31 May 2004(2004-05-31) (aged 86)Oroville, California, United States[1]ReligionThelemaNationalityAmericanLineageA∴A∴ lineage of Soror EstaiKnown forRe-establishment of O.T.O., empowerment of women in ThelemaProfessionTeacherOrganizationTempleLodge 418OrderOrdo Templi OrientisChurchEcclesia Gnostica CatholicaFounder ofCollege of Thelema...

