קוד ליניארי
|
Read other articles:

Pratyusha BanerjeeLahir(1991-08-10)10 Agustus 1991[1][2]Jamshedpur, Bihar (sekarang Jharkhand), IndiaMeninggal1 April 2016(2016-04-01) (umur 24)Andheri, Mumbai, Maharashtra, IndiaSebab meninggalBunuh diriKebangsaanIndianPekerjaanActressTahun aktif2003–2016Dikenal atasAnandhi, Bigg Boss 7, Hum Hain Na, Sasural Simar Ka Pratyusha Banarjee (10 Agustus 1991 – 1 April 2016) adalah Aktris asal India. Ia dikenal sebagai Anandhi diserial Balika Vadhu....

Ángel Ángel berlaga untuk LevanteInformasi pribadiNama lengkap Ángel Luis Rodríguez DíazTanggal lahir 26 April 1987 (umur 36)Tempat lahir Santa Cruz de Tenerife, SpanyolTinggi 1,72 m (5 ft 8 in)Posisi bermain PenyerangInformasi klubKlub saat ini EibarNomor 9Karier junior TenerifeKarier senior*Tahun Tim Tampil (Gol)2005–2006 Tenerife B 2006–2010 Tenerife 103 (16)2007 → Real Madrid B (pinjaman) 3 (0)2008 → Osasuna B (pinjaman) 17 (4)2010–2012 Elche 66 (28)2012–2...

Caponata Pasta alla norma Masakan Sisilia (cucina siciliana) adalah jenis masakan Italia yang berasal dari Pulau Sisilia di Italia Selatan. Kuliner rakyat Pulau Sisilia dipengaruhi oleh iklim Mediterania dan memiliki variasi yang beragam karena bahan-bahannya dihasilkan dari laut maupun daratan. Masakan Sisilia dianggap sebagai salah satu variasi masakan Italia yang paling dikenal karena citarasanya yang bermacam-macam. Sejarah masakan Sisilia dipengaruhi oleh bangsa-bangsa yang menetap di sa...

Bergschenhoek Desamunicipality seat (en)munisipalitas di Belandacadastral populated place in the Netherlands (en) Bergschenhoek (nl) flag of Bergschenhoek (en) coat of arms of Bergschenhoek (en) Tempat categoria:Articles mancats de coordenades Negara berdaulatKerajaan BelandaCountry of the Kingdom of the Netherlands (en)BelandaProvinsi di BelandaHolland SelatanMunisipalitas di BelandaLansingerland NegaraBelanda PendudukTotal970 (1830 )GeografiLuas wilayah14,89 km² [convert: unit t...
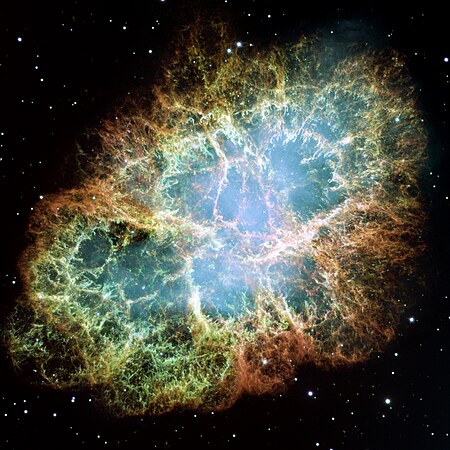
Nebula Kepiting merupakan sisa-sisa dari supernova SN 1054, gambar diambil oleh Teleskop Hubble. SN 1054 adalah supernova yang pertama kali yang diamati pada tanggal 4 Juli 1054, dan tetap terlihat selama dua tahun. Tanggal pasti telah disengketakan tetapi sebagian besar akun menerima tanggal Tiongkok pada 4 Juli. Peristiwa itu direkam dalam sebuah dokumen dari dunia arab, dalam astronomi komtemporer Tiongkok, dan rujukannya juga ditemukan dalam dokumen Jepang kemudian (abad ke 13). Supernova...

Kisah Hidup Paman GoberSampul bukunya yang ber-bahasa Inggris Kisah Hidup Paman Gober atau The Life and Times of Scrooge McDuck adalah sebuah komik berseri yang dibuat oleh Don Rosa tentang Gober Bebek. Pada awalnya, cerita ini hanya dibuat sebanyak 12 bab dan berjumlah 212 halaman yang berjudul: The Last of the Clan Mcducks (Keturunan terakhir keluarga bebek) The Master of the Mississippi (Jagoan sungai Mississippi) The Buckaroo of the Badlands (Jagoan perbukitan karang) Raider of the Cooper...

For other uses, see Mirzapur (disambiguation). Census Town in West Bengal, IndiaMirzapurCensus TownMirzapurLocation in West Bengal, IndiaShow map of West BengalMirzapurMirzapur (India)Show map of IndiaCoordinates: 24°24′33″N 88°04′04″E / 24.4091°N 88.0679°E / 24.4091; 88.0679StateWest BengalDistrictMurshidabadArea • Total2.8534 km2 (1.1017 sq mi)Population (2011) • Total6,081 • Density2,100/km2 (5,500/...

Tank Cruiser Mk I (A9)Tank Cruiser Mk I (A9)Karakteristik umumAwak6 orang (komandan, penembak, pengisi peluru, pengemudi, 2 org penembak MG)Panjang5.8 mLebar2.5 mTinggi2.65 mBerat12 tonPerlindungan dan persenjataanKetebalan baja6 - 14 mmSenjata utamaQF 2 pounder - 100 putaranSenjata pelengkap3 x Senapan Mesin Vickers kaliber 0.303 - 3000 putaranMobilitasMesinAEC 179 - 6 silinder diesel (150 dk (daya kuda))Suspensisprung (tipe bogie 3 roda)Kecepatan40 km/jDaya jelajah241 kmlbs Cruiser Mk I ata...

Class of organic compounds Not to be confused with Glycan. A glucan is a polysaccharide derived from D-glucose,[1] linked by glycosidic bonds. Glucans are noted in two forms: alpha glucans and beta glucans. Many beta-glucans are medically important. They represent a drug target for antifungal medications of the echinocandin class. Types The following are glucans (The α- and β- and numbers clarify the type of O-glycosidic bond and the specific carbons involved):[2] Alpha Main...

American businesswoman and government official (1905–1995) Oveta Culp Hobby1st United States Secretary of Health, Education, and WelfareIn officeApril 11, 1953 – July 31, 1955PresidentDwight D. EisenhowerPreceded byHerself (Federal Security Agency Administrator)Succeeded byMarion B. FolsomAdministrator of the Federal Security AgencyIn officeJanuary 20, 1953 – April 11, 1953PresidentDwight D. EisenhowerPreceded byOscar EwingSucceeded byHerself (Health, Education and Wel...

CourmascomuneCourmas – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Marna ArrondissementReims CantoneFismes-Montagne de Reims TerritorioCoordinate49°11′N 3°54′E / 49.183333°N 3.9°E49.183333; 3.9 (Courmas)Coordinate: 49°11′N 3°54′E / 49.183333°N 3.9°E49.183333; 3.9 (Courmas) Superficie2,85 km² Abitanti177[1] (2009) Densità62,11 ab./km² Altre informazioniCod. postale51390 Fuso orarioUTC+1 Codice ...

In mathematics, the split-octonions are an 8-dimensional nonassociative algebra over the real numbers. Unlike the standard octonions, they contain non-zero elements which are non-invertible. Also the signatures of their quadratic forms differ: the split-octonions have a split signature (4,4) whereas the octonions have a positive-definite signature (8,0). Up to isomorphism, the octonions and the split-octonions are the only two 8-dimensional composition algebras over the real numbers. They are...

Stadion Talang JimarTribun utama Stadion Talang Jimar. Informasi stadionPemilikPemerintah Kota PrabumulihOperatorPT Pantja Djaja Ranau[1]LokasiLokasiKelurahan Prabumulih, Kecamatan Prabumulih Selatan, Kota Prabumulih, Sumatera Selatan, IndonesiaKoordinat3°27′25″S 104°15′14″E / 3.456862°S 104.253916°E / -3.456862; 104.253916Direnovasi2019Biaya pembuatanRp. 10 miliarPemakaiPersipra PrabumulihSunting kotak info • L • BBantuan penggunaan t...

20th century Imperial Chinese Army Beiyang Army北洋軍Symbol of the Beiyang ArmyActive1895–1928Country Qing Empire Republic of China (Beiyang government)TypeArtilleryCavalryInfantrySize20,000 (1901)60,000 (1905)Garrison/HQTianjinEngagements First Sino-Japanese War Xinhai Revolution Occupation of Mongolia Northern Expedition CommandersNotable commandersYuan ShikaiDuan QiruiYinchangFeng GuozhangMilitary unit The Beiyang Army (Chinese: 北洋軍; pinyin: Běi Yáng Jūn; lit. &#...

Arden ChoCho tahun 2019Lahir16 Agustus 1985 (umur 38)Amarillo, Texas, U.S.AlmamaterUniversitas Illinois di Urbana–Champaign (BA)PekerjaanModelPemeranPenyanyiTahun aktif2006–sekaramgAgenSeniman Inovatif Arden Cho[1] (lahir 16 Agustus 1985) adalah pemeran berkebangsaan amerika, penyanyi dan seorang peragawati yang terkenal karena memerankan Kira Yukimura pada series Teen Wolf pada tahun 2011.[2][3] Dia juga memainkan peran utama dalam film pendek tahun 201...

Airline based in Sint Maarten This article is about the Netherlands Antilles airline. For the former United States charter airline, see WinAir Airlines. Winair IATA ICAO Callsign WM WIA WINDWARD FoundedAugust 24, 1961[1]Commenced operationsJuly 5, 1962[1]HubsPrincess Juliana International AirportAllianceCaribsky[2]Fleet size6Destinations12HeadquartersPrincess Juliana International Airport, Philipsburg, Sint MaartenKey peopleHans van de Velde (CEO)[3]Founders Ge...

Johann Strauss II LahirJohann Baptist Strauss25 Oktober 1825Wina, AustriaMeninggal3 Juni 1899 (Umur 74 tahun)Wina, Austria-HungariaMakamPemakaman pusat WinaPekerjaanKomposerSuami/istriHenrietta Treffz (1862–1878), Angelika DittrichOrang tuaJohann Strauss I (bapak)Tanda tangan Johann Strauss II (Bahasa Jerman: Johann Strauß (Sohn); atau Johann Strauss Jr., Johann Sebastian Strauss) (25 Oktober 1825 – 3 Juni 1899) adalah komponis Austria yang dikenal terutama untuk karya musik waltz-nya, ...

Imperial Korean officer (1869–1907) In this Korean name, the family name is Park. Park Seung-hwan박승환Born(1869-09-07)September 7, 1869Hanseong, Gyeonggi, KoreaDiedAugust 1, 1907(1907-08-01) (aged 37)Hanseong, Gyeonggi, KoreaAllegiance KoreaBranch Imperial Korean ArmyYears of service1897 – 1907RankMajorKnown forOrganizing the Battle of Namdaemun Park Seung-hwan (Korean: 박승환) was a Korean military officer and independence activist of the Korean E...

Questa voce sull'argomento centri abitati della prefettura di Gifu è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Yamagatacittà山県市 Yamagata – Veduta LocalizzazioneStato Giappone RegioneChūbu Prefettura Gifu SottoprefetturaNon presente DistrettoNon presente TerritorioCoordinate35°30′20.2″N 136°46′53.2″E35°30′20.2″N, 136°46′53.2″E (Yamagata) Superficie222,04 km² Abitanti29 903 (1-10-2007) Densità134,...

Abdulmalek Al-Khaibri Abdulmalek Al-Khaibri (2018)Informasi pribadiNama lengkap Abdulmalek Al-KhaibriTanggal lahir 13 Maret 1986 (umur 38)Tempat lahir Riyadh, Arab SaudiTinggi 177 cm (5 ft 10 in)Posisi bermain GelandangInformasi klubKlub saat ini Al-Hilal FCNomor 6Karier senior*Tahun Tim Tampil (Gol)2016 – Al-Hilal FC 21 (0)Tim nasional2011 – Arab Saudi 33 (0) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Abdulmalek Al-Khaibri (lahir 13 Maret 1...





![{\displaystyle \ [n,k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01b16889cd2ed42a1ab16c7486fbafaf7c05b3ea)



![{\displaystyle [n,k,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef7bd63229a2d74455e0037c5d70d39a13184a75)
![{\displaystyle [n,k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d9e3e5f03db243c10e64608605d156ae1885952)




























