פונקציה כוכבית
|
Read other articles:

Madison Cawthorn David Madison Cawthorn (lahir 1 Agustus 1995) adalah seorang politikus asal Amerika Serikat. Sebagai anggota Partai Republik, Cawthorn menjadi anggota DPR setelah memenangkan pemilu 2020.[1] Ia adalah anggota termuda di Kongres sejak Jed Johnson Jr. dan anggota Kongres pertama yang lahir pada 1990an.[2] Referensi ^ North Carolina Election Results: 11th Congressional District. The New York Times (dalam bahasa Inggris). ISSN 0362-4331. Diarsipkan dari versi...

Howard Philips LovecraftLahir20 Agustus 1890Providence, Rhode Island, Amerika SerikatMeninggal15 Maret 1937(1937-03-15) (umur 46)Providence, Rhode IslandPekerjaanPenulisKebangsaanAmerika SerikatGenreHoror, fantasi, fiksi ilmiah Howard Phillips Lovecraft (20 Agustus 1890 – 15 Maret 1937), singkatan H. P. Lovecraft, adalah penulis horor, fantasi dan fiksi ilmiah, khususnya subgenre yang dikenal sebagai fiksi aneh.[1] Prinsip estetis dan filosofis dari Lovecraft adal...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2023. Boboy adalah sebuah grup musik populer di Malaysia pada tahun 2001 yang menyampaikan lagu-lagu lagu Berbahasa Melayu. Lagu hit adalah Episod cinta, Dalam Benci Ada Rindu, Memori Cinta dan Demi Masa. Di awal kemunculan grup ini yaitu sekitar penghujung 19...

Gullfoss Gullfoss Gullfoss ialah air terjun yang terletak di Sungai Putih (Hvítá) di Islandia selatan-tengah. Namanya berarti Air Terjun Emas. Aliran sungai dari hujan berkala dan luncuran gletser-khususnya di musim panas-membuat Gullfoss air terjun bervolume terbesar di Eropa. Gullfoss ialah salah satu pemandangan spektakuler di bumi. Merupakan salah satu keajaiban dunia alami di dunia. Sungai Putih (Hvita) yang luas mengalir ke selatan. Sekitar 1 km di atas air terjun sungai itu memb...

Katedral Basilika Minor Bunda dari Altagracia Ini adalah daftar basilika di Republik Dominika. Katolik Daftar basilika Gereja Katolik di Republik Dominika[1]: Katedral Basilika Minor Bunda dari Altagracia Basilika Katedral Metropolitan Santa Maria dari Inkarnasi (Katedral Primasial Amerika), Santo Domingo Lihat juga Gereja Katolik Roma Gereja Katolik di Republik Dominika Daftar katedral di Republik Dominika Daftar basilika Referensi ^ Basilika di seluruh dunia lbsDaftar basilika di Am...

American politician Ron DunnDunn in 2022Member of the New Hampshire House of Representativesfrom the Rockingham 16th districtIncumbentAssumed office December 7, 2022 Personal detailsPolitical partyRepublican[1] Ron Dunn is an American politician. He serves as a Republican member for the Rockingham 16th district of the New Hampshire House of Representatives.[2] References ^ NH House Rockingham County District 16: Elected Officials. CitizensCount. Retrieved Febru...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Robot – berita · surat kabar · buku · cendekiawan · JSTOR (November 2013) Sophia, robot pertama yang memiliki status kewarganegaraan seperti manusia Robot humanoid yang tersenyum dan berpose bersama seorang w...

Indian television series Shaurya Aur Anokhi Ki KahaniGenreDramaRomanceDeveloped byLeena GangopadhyayWritten bySatyam TripathiMunisha RajpalRajesh RajpalScreenplay byIla Bedi DuttaDamini Kanwal ShettyBhavna VyasStory byIla Bedi DuttaMitali BhattacharyaDamini Kanwal ShettyDirected byImtiaz PunjabiSamir KulkarniRakesh KumarVikram GhaiCreative directorManjari MukulStarringDebattama SahaKaranvir SharmaTheme music composerSargam JassuNakash AzizComposerKingshuk ChakravartyCountry of originIndiaOrig...

Said bin al-Musayyib bin Hazn bin Abi Wahb al-Makhzumi al-Quraisy (Arab: سعيد بن المسيب بن حزن بن أبي وهب المخزومي القرشيcode: ar is deprecated , lahir 15 H/636, wafat 94 H/715 M; umur 79 tahun) adalah salah seorang ulama ahli hadits dan ahli fiqih dari Madinah.[1][2] Ia termasuk golongan tabi'in, dan merupakan salah seorang dari Tujuh Fuqaha Madinah.[3][4][5] Di antara ketujuh tokoh Madinah tersebut, Said sering ...
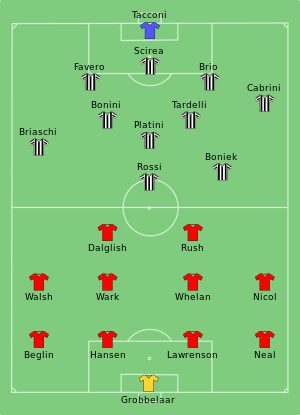
This article is about the match. For the pre-match incidents, see Heysel Stadium disaster. Football match1985 European Cup finalMatch programme coverEvent1984–85 European Cup Juventus Liverpool 1 0 Date29 May 1985VenueHeysel Stadium, BrusselsRefereeAndré Daina (Switzerland)Attendance58,000← 1984 1986 → The 1985 European Cup final was an association football match between Liverpool of England and Juventus of Italy on 29 May 1985 at the Heysel Stadium, Brussels, Belgium. It was t...

John Barnardiston by Frans van der Mijn John Barnardiston (1719–1778) was the principal librarian (protobibliothecarius) of the University of Cambridge from 1769 to 1778 and the Master of Corpus Christi College, Cambridge from 1764 until 1778. He was educated at Tonbridge School; matriculated as a sizar of Corpus Christi in 1737; and was awarded four university degrees: B.A. (1740/41); M.A. (1744); B.D. (1752); and D.D. (1764). He was a Fellow of Corpus Christi from 1745 to 1759, and becam...

这是马来族人名,“阿末”是父名,不是姓氏,提及此人时应以其自身的名“祖基菲里”为主。 尊敬的拿督斯里哈芝祖基菲里·阿末Dzulkefly bin Ahmad国会议员、DGSM博士 马来西亚卫生部部长现任就任日期2023年12月12日君主最高元首苏丹阿都拉最高元首苏丹依布拉欣·依斯迈首相安华·依布拉欣副职卡尼斯曼(英语:Lukanisman Awang Sauni)前任扎丽哈·慕斯达法任期2018年5月21日—2...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目的语调或风格或許不合百科全書。 (2024年1月29日)請根據指南協助改善这篇条目,並在讨论页討論問題所在,加以改善。 此生者传记条目需要补充更多可供查證的来源。 (2024年1月29日)请协助補充可靠来源,无法查证的在世人物内容将被立即移除。 此条目页的主題是中华人民共和国现任国...

Hotel Petersberg. Les missions ou tâches de Petersberg sont une série de missions décidées en 1992 à Petersberg (près de Bonn, en Allemagne), par les États membres de l'Union de l'Europe occidentale (UEO) pour décider quelles actions de défense ils pourraient entreprendre ensemble, en coopération avec l'Union européenne (dont tous les membres de l'UEO font partie) et avec l'OTAN. Ce concept a été repris par l'Union européenne qui englobait les 10 États membres de l'UEO et progr...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Campomarino – news · newspapers · books · scholar · JSTOR (November 2013) Comune in Molise, ItalyCampomarino KëmariniComuneComune di Campomarino Coat of armsLocation of Campomarino CampomarinoLocation of Campomarino in ItalyShow map of ItalyCampomari...

This article is about the Greek political party. For political parties in Russia, see Political parties in Russia. Political party in Greece Napist Party κόμμα των ΝαπαίωνHistorical leadersAugustinos KapodistriasAndreas MetaxasKitsos TzavelasTheodoros KolokotronisKonstantinos KanarisNikitaras StamatelopoulosAlexandros KoumoundourosFounded1827 (1827)Dissolved1865 (1865)Merged intoNationalist PartyHeadquartersAthensIdeologyPopulism[1]Centralization[...

Kali Krukut adalah sungai sepanjang kurang dari 40 km yang mengalir dari Situ Citayam, Bogor, Depok, Jagakarsa, Cilandak, Pasar Minggu, Kemang, Mampang Prapatan, Gatot Subroto, Setiabudi, Tanah Abang, Pecinan Glodok, bercabang di bawah Jembatan Toko Tiga Pancoran, melewati Pertokoan Gloria sampai di Bawah Jembatan Harco, hingga berakhir di Banjir Kanal Barat (menyatu dengan Kali Ciliwung).[1] Awalnya Kali Krukut merupakan sungai yang bersih dan menjadi tujuan wisata di bawah peme...

Navigable international boundary waterway connecting Juan de Fuca and Georgia Straits Haro StraitFrench: Détroit de HaroView of Haro Strait from South Pender IslandHaro StraitMap of Haro Strait and Boundary Pass according to USGS definitionsLocationBritish Columbia and WashingtonCoordinates48°33′N 123°13′W / 48.550°N 123.217°W / 48.550; -123.217TypeStraitPart ofSalish SeaBasin countriesCanada and United StatesMax. length36 km (22 mi)Max. wi...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Historia de Tanzania» – noticias · libros · académico · imágenesEste aviso fue puesto el 25 de enero de 2016. Mapa del África Oriental Alemana, del año 1894. Lo que hoy es Tanzania fue una colonia alemana conocida como África Oriental Alemana desde alrededor de 1880 hasta 1919. Estuvo bajo control del Reino Unido entre 1919 y 1961. Poco después de la in...

Municipality in Brazil For other uses of Pereira, see Pereira (disambiguation). Municipality in Southeast, BrazilPereira BarretoMunicipality FlagCoat of armsLocation in São Paulo statePereira BarretoLocation in BrazilCoordinates: 20°38′18″S 51°6′33″W / 20.63833°S 51.10917°W / -20.63833; -51.10917CountryBrazilRegionSoutheastStateSão PauloArea • Total974 km2 (376 sq mi)Population (2020 [1]) • Total25,677&#...



























