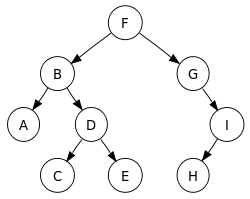
עץ חיפוש
| ||||||||||||
Read other articles:

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: 12 Sweet Memories Panbers – berita · surat kabar · buku · cendekiawan · JSTOR Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan...

Kucica hutan Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Passeriformes Famili: Muscicapidae Genus: Copsychus Spesies: C. malabaricus Nama binomial Copsychus malabaricusScopoli, 1788) Sinonim Kittacincla macruraCittocincla macrura Kucica Hutan (Copsychus malabaricus) juga dikenal sebagai Murai Batu termasuk ke dalam famili Muscicapidae atau burung cacing. Tersebar di seluruh pulau Sumatra, Semenanjung ...

Study of the methods of historians Study of history redirects here. For the book by Toynbee, see A Study of History. Historical school redirects here. For the approach to economics, see Historical school of economics. For the movement in jurisprudence, see German Historical School. The Allegory On the Writing of History shows Truth watching the historian write history, while advised by Wisdom. (Jacob de Wit,1754) Historiography is the study of the methods of historians in developing history a...

روتنبورغ أن در فولدا شعار الإحداثيات 50°59′42″N 9°43′38″E / 50.995°N 9.7272222222222°E / 50.995; 9.7272222222222 [1] تقسيم إداري البلد ألمانيا[2][3] خصائص جغرافية المساحة 79.97 كيلومتر مربع (31 ديسمبر 2017)[4] ارتفاع 183 متر عدد السكان عدد السكان 140...

Untuk sejarah situs ini lihat dalam urutan kronologi: Maresa (Maresha), Beit Guvrin, Eleuteropolis, Bethgibelin, Beit Jibrin, Kibbutz Beit Guvrin dan Taman Nasional Beit Guvrin Gua-gua MaresaCaves of MareshaSitus Warisan Dunia UNESCOMaresa: Pekuburan UtaraLokasiSefela, Israel,Bagian dariGua-gua Maresa dan Bet-Guvrin di dataran rendah Yudea sebagai suatu Microcosmos Tanah Gua-gua (Land of the Caves)KriteriaKebudayaan: (v)Nomor identifikasi1370Pengukuhan2014 (Sesi ke-38)Koordinat31°35′3...

Voce principale: L.R. Vicenza. S.S. Lanerossi VicenzaStagione 1984-1985Una formazione del L.R. Vicenza Sport calcio SquadraVicenza Calcio Allenatore Bruno Giorgi Presidente Dario Maraschin Serie C12º (In Serie B)[1] Coppa ItaliaFase a gironi Coppa Italia Serie COttavi di finale 1983-1984 1985-1986 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti la Società Sportiva Lanerossi Vicenza nelle competizioni ufficiali della stagione 1984-1985. Indic...

KayshaEdward Mokolo Jr.Background informationBirth nameEdward Mokolo Jr.Born1974Kinshasa, ZaireGenresKizombazoukafropopafro houseR&BOccupation(s)SingerrapperbusinessmanproducerYears active1992–presentLabelsSushirawMusical artist Edward Mokolo Jr. (born 1974), better known as Kaysha, is a singer/rapper and producer from the Democratic Republic of the Congo (former Zaire). He is the son of Congolese politician Édouard Mokolo Wa Mpombo. Career He was born in Kinshasa, Zaire but emigrated...

Untuk kegunaan lain, lihat Arakawa dan Arakawa. Arakawa 荒川区Distrik kota istimewa BenderaLambangLokasi Arakawa di Prefektur TokyoNegara JepangWilayahKantōPrefektur TōkyōPemerintahan • Wali kotaTaiichirō NishikawaLuas • Total10,2 km2 (39 sq mi)Populasi (Oktober 1, 2015) • Total212.264 • Kepadatan20,810/km2 (53,90/sq mi)Zona waktuUTC+9 (WSJ)Kode pos116-8501Simbol • PohonSakura• BungaRhododendron...

Georgie HenleyHenley pada saat premiere The Chronicles of Narnia: Prince Caspian di InggrisLahirGeorgina Laura Henley/Georgina Helen HenleyNama lainGeorgiePenghargaanPhoenix Film Critics Society Award for Best Performance by a Youth in a Lead or Supporting Role — Female2006 The Chronicles of Narnia: The Lion, the Witch and the WardrobeYoung Artist Award for Best Performance in a Feature Film — Young Actress Age Ten or Younger2006 The Chronicles of Narnia: the Lion, the Witch and the...

Bagian dari seriIslam Rukun Iman Keesaan Allah Malaikat Kitab-kitab Allah Nabi dan Rasul Allah Hari Kiamat Qada dan Qadar Rukun Islam Syahadat Salat Zakat Puasa Haji Sumber hukum Islam al-Qur'an Sunnah (Hadis, Sirah) Tafsir Akidah Fikih Syariat Sejarah Garis waktu Muhammad Ahlulbait Sahabat Nabi Khulafaur Rasyidin Khalifah Imamah Ilmu pengetahuan Islam abad pertengahan Penyebaran Islam Penerus Muhammad Budaya dan masyarakat Akademik Akhlak Anak-anak Dakwah Demografi Ekonomi Feminisme Filsafat...
Period in the history of Sri Lanka during the Anuradhapura Kingdom (377 BC-1017 AD) Main articles: History of Sri Lanka and Anuradhapura Kingdom Anuradhapura period377 BCE – 1017Gilded bronze statue of the Bodhisattva Tara, dated to the 8th century, found in the eastern coast of Sri LankaIncluding Early Anuradhapura period Middle Anuradhapura period Late Anuradhapura period Monarch(s) House of Vijaya The Five Dravidians House of Lambakanna I The Six Dravidians House of Moriya House...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

Neighbourhood in Montreal, Quebec, CanadaChinatown Quartier chinoisNeighbourhoodThe paifang on Saint Laurent BoulevardChinatownLocation of Chinatown in MontrealCoordinates: 45°30′27″N 73°33′39″W / 45.50759°N 73.5608°W / 45.50759; -73.5608CountryCanadaProvinceQuebecCityMontrealBoroughVille-MarieEstablishedEarly 1890s[1]Elevation70 ft (20 m)Postal CodeH2ZArea code(s)514, 438 Chinatown in Montreal (French: Quartier chinois de Montréal; simpl...

جزء من سلسلة مقالات عنالهندوسية هندوس تاريخ آلهة تريمورتي براهما فيشنو شيفا الديفي والديفا ساراسواتي لاكشمي بارفاتي شاكتي دورغا كالي غانيشا سوبراهمانيا آيابا راما كريشنا هانومان براجاباتي رودرا إندرا آجني ديوس بهومي فارونا فايو فلسفةمفاهيم براهمان أوم إشفارا أتمان ماي...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

This article is about the Bobby Brown album. For other albums with similar titles, see Masterpiece (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Masterpiece album – news · newspapers · books · scholar · JSTOR (August 2012) (Learn how and when to remove this message) 2012 studio a...

Unit of length; one millionth of a metre Micron redirects here. For other uses, see Micron (disambiguation). Microscale redirects here. For other uses, see Microscale (disambiguation). For the measuring instrument, see Micrometer (device). μm redirects here. For the chemical unit μM, see Micromolar. micrometreA 6 μm diameter carbon filament above a 50 μm diameter human hairGeneral informationUnit systemSIUnit oflengthSymbolμmConversions 1 μm in ...... is equal to ......

Voce principale: Verein für Leibesübungen Bochum 1848. Verein für Leibesübungen Bochum 1848Stagione 2021-2022Sport calcio Squadra Bochum Allenatore Thomas Reis All. in seconda Heiko Butscher Markus Gellhaus Frank Heinemann Bundesliga13º posto Coppa di GermaniaQuarti di finale Maggiori presenzeCampionato: Losilla, Polter (33)Totale: Losilla (37) Miglior marcatoreCampionato: Polter (10)Totale: Polter (11) StadioVonovia Ruhrstadion Maggior numero di spettatori25 000 vs. Borussia ...

Radek ŠtěpánekKebangsaan CekoTempat tinggalMonte Carlo, MonakoLahir27 November 1978 (umur 45)Karviná, Cekoslowakia(sekarang Ceko)Tinggi185 m (606 ft 11 in)Memulai pro1996Pensiun2017Tipe pemainTangan kanan (two-handed backhand)Total hadiahUS$11,343,464TunggalRekor (M–K)384–302 (55.98%) (ATP and Grand Slam level, and in Davis Cup)Gelar5Peringkat tertinggiNo. 8 (10 Juli 2006)Hasil terbaik di Grand Slam (tunggal)Australia Terbuka3R (2003, 2005, 2007, 2009, 2013)Pr...

American actor (1931-2005) For other people named Brian Kelly, see Brian Kelly (disambiguation). Brian KellyKelly in c.1966Born(1931-02-14)February 14, 1931Detroit, Michigan, U.S.DiedFebruary 12, 2005(2005-02-12) (aged 73)Voorhees Township, New Jersey, U.S.Resting placeNew Jersey, U.S.Alma materUniversity of Notre Dame (1953)University of Michigan Law SchoolOccupation(s)Actor, producerYears active1958–1996Spouses Laura Devon (m. 1962; div.&...