ОъОАОцОе ОъОЕОЋОЏОюОю
|
Read other articles:

Tetesan getah yang keluar dari kulit pohon yang terluka Getah adalah istilah umum untuk menyebut cairan agak cair sampai kental yang keluar organ tumbuhan maupun hewan (getah alami) atau residu sistem mesin.[1] Getah pada umumnya mengeras setelah beberapa waktu karena mengalami kondensasi. Pada hewan, getah digunakan untuk menyebut cairan limfatik (getah bening). Pada tumbuhan, getah adalah segala sesuatu yang bersifat agak cair sampai kental yang keluar dari batang, daun, bunga, atau...

English peer in the War of the Roses (1428РђЊ1471) Richard Neville16th Earl of WarwickWarwick as drawn in the Rous Roll. He displays on his shield the arms of Montagu quartering Monthermer. The bull's head is the crest of the Neville family, the eagle is the crest of Montagu.Tenure23 July 1449[1] РђЊ 14 April 1471PredecessorAnne Beauchamp, 15th Countess of WarwickSuccessorEdward Plantagenet, 17th Earl of WarwickOther titles6th Earl of Salisbury8th and 5th Baron Montagu7th Baron Monthe...

Peta infrastruktur dan tata guna lahan di Komune Armenti├еres-en-Brie. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiArmenti├еres-en-BrieNegaraPrancisArondisemenMeauxKantonLizy-sur-OurcqAntarkomuneCommunaut├Е de communes du Pays de l'OurcqPemerintahan Рђб Wali kota (2008-2014) Claudine Courtial Рђб Populasi11.256Kode INSEE/pos77008 / 2 Po...

1574 battle Conquest of TunisPart of the Ottoman-Habsburg warsThe Ottoman fleet attacking Tunis at La Goulette in 1574.Date12 July РђЊ 13 September 1574[1]LocationTunisResult Ottoman victoryTerritorialchanges Ottomans capture TunisBelligerents Spanish Empire Ottoman EmpireCommanders and leaders Gabrio Serbelloni (POW) Occhiali[1] C─▒─Ъalazade Yusuf Sinan Pasha[1]Strength Total men: 7,000 250РђЊ300 warshipsTotal men: 100,000Casualties and losses 6,700 killed, 300 p...

Questa voce o sezione sull'argomento edizioni di competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. T├╝rkiye 1.Lig 1995-1996 Competizione T├╝rkiye 1.Lig Sport Calcio Edizione 38┬ф Organizzatore TFF Luogo Turchia Partecipanti 18 Formula 1 girone all'italiana Risultati Vincitore ...

Governor of South Dakota from 1947 to 1951 George T. MickelsonChief Judge of the United States District Court for the District of South DakotaIn office1954РђЊ1965Preceded byOffice establishedSucceeded byAxel J. BeckJudge of the United States District Court for the District of South DakotaIn officeDecember 9, 1953 РђЊ February 28, 1965Appointed byDwight D. EisenhowerPreceded bySeat established by 65 Stat. 710Succeeded byFred Joseph Nichol18th Governor of South DakotaIn officeJanua...

Рђа лДлхл╗лЙл▓лхл║ л┐ЛђЛЈл╝лЙЛЁлЙл┤ЛЈЛЅлИл╣ лЮл░ЛЃЛЄлйл░ЛЈ л║л╗л░ЛЂЛЂлИЛёлИл║л░ЛєлИЛЈ лћлЙл╝лхлй:лГЛЃл║л░ЛђлИлЙЛѓЛІлдл░ЛђЛЂЛѓл▓лЙ:лќлИл▓лЙЛѓлйЛІлхлЪлЙл┤Лєл░ЛђЛЂЛѓл▓лЙ:лГЛЃл╝лхЛѓл░лилЙлИлЉлхли Лђл░лйл│л░:лћл▓ЛЃЛЂЛѓлЙЛђлЙлйлйлх-ЛЂлИл╝л╝лхЛѓЛђлИЛЄлйЛІлхлЉлхли Лђл░лйл│л░:лњЛѓлЙЛђлИЛЄлйлЙЛђлЙЛѓЛІлхлблИл┐:лЦлЙЛђл┤лЙл▓ЛІлхлЪлЙл┤ЛѓлИл┐:лЪлЙлил▓лЙлйлЙЛЄлйЛІлхлўлйЛёЛђл░ЛѓлИл┐:лДлхл╗ЛјЛЂЛѓлйлЙЛђлЙЛѓЛІлхлЮл░л┤л║л╗л░ЛЂЛЂ:лДлхЛѓл▓лхЛђлЙлйлЙл│лИлхлџл╗л░л┤л░:лљл╝лйлИлЙЛѓЛІлџл╗л░л┤л░:лАлИлйл░л┐ЛЂлИл┤ЛІ№┐й...

Remote desktop software tool This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Chrome Remote Desktop РђЊ news ┬и newspapers ┬и books ┬и scholar ┬и JSTOR (April 2014) (Learn how and when to remove this template message) Chrome Remote DesktopDeveloper(s)GoogleInitial releaseOctober 8, 2011; 12 years ago (2011-10-08)[1]Stable release120.0...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Alip Ba TaInformasi pribadiLahirAlif Gustakhiyat21 Juni 1989 (umur 34)Ponorogo, Jawa Timur, IndonesiaPekerjaanGitaris, Pencipta laguInformasi YouTubeKanal Alip_Ba_Ta Tahun aktif2018РђЊsekarangGenreSemua genrePelanggan5.77 juta[1]Tota...

2010 American League Division SeriesTeamsTeam (Wins) Manager SeasonTexas Rangers (3) Ron Washington 90РђЊ72, .556, GA: 9Tampa Bay Rays (2) Joe Maddon 96РђЊ66, .593, GA: 1DatesOctober 6 РђЊ 12TelevisionTBSTV announcersDon Orsillo Buck Martinez and (Marc Fien)RadioESPNRadio announcersDan Shulman and Bobby ValentineUmpiresTim Welke, Jim Wolf, Jerry Meals, Bill Miller, Jeff Kellogg and Mike DiMuro.[1]TeamsTeam (Wins) Manager SeasonNew York Yankees (3) Joe Girardi 95РђЊ67, .586,...

Questa voce sull'argomento politici paraguaiani ├е solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Bernardino Caballero 9┬║ Presidente del ParaguayDurata mandato4 settembre 1880 –25 novembre 1886 Vice presidenteJuan Antonio Jara PredecessoreC├Аndido Bareiro SuccessorePatricio Escobar Dati generaliPartito politicoPartido Colorado (Paraguay) Bernardino Caballero de A├▒asco y Melgarejo (Ybycu├Г, 20 maggio 1839 РђЊ Asunci├│n, 26 feb...

ТГцТбЮуЏ«тЈ»тЈѓуЁДтцќУфъуХГтЪ║уЎЙуДЉуЏИТЄЅТбЮуЏ«ТЮЦТЅЕтЁЁсђѓУІЦТѓеуєЪТѓЅТЮЦТ║љУ»ГУеђтњїСИ╗жбў№╝їУ»итЇЈтіЕтЈѓУђЃтцќУ»Гу╗┤тЪ║уЎЙуДЉТЅЕтЁЁТЮАуЏ«сђѓУ»итІ┐уЏ┤ТјЦТЈљС║цТю║Тб░у┐╗У»Љ№╝їС╣ЪСИЇУдЂу┐╗У»ЉСИЇтЈ»жЮасђЂСйјтЊЂУ┤етєЁт«╣сђѓСЙЮуЅѕТЮЃтЇЈУ««№╝їУ»ЉТќЄжюђтюеу╝ќУЙЉТЉўУдЂТ│еТўјТЮЦТ║љ№╝їТѕќС║јУ«еУ«║жАхжАХжЃеТаЄУ«░{{Translated page}}ТаЄуГЙсђѓ OsagyefoтЁІуЊду▒│┬иТЂЕтЁІж▓ЂујЏуггСИЅт▒іжЮъТ┤▓УЂћуЏЪСИ╗тИГС╗╗ТюЪ1965т╣┤10Тюѕ21ТЌЦРђћ1966т╣┤2Тюѕ24ТЌЦтЅЇС╗╗У┤ЙУ┐ѕтІњ┬ижў┐тЇюТЮю-у║│УхЏт░ћу╗ДС╗╗у║дуЉЪтцФ┬иС║џуЉЪ┬и№┐й...

Collection of multimedia related APIs on Microsoft platforms DX9 redirects here. For the synthesizer, see Yamaha DX9. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: DirectX РђЊ news ┬и newspapers ┬и books ┬и scholar ┬и JSTOR (April 2016) (Learn how and when to remove this message) DirectXDeveloper(s)MicrosoftInit...

пД┘ёп«п»┘і┘ѕ┘і пф┘ѕ┘Ђ┘і┘ѓ п«п»┘і┘ѕ┘і ┘Ёпхп▒ пД┘ёп«п»┘і┘ѕ┘і пф┘ѕ┘Ђ┘і┘ѓ ┘Ђпфп▒пЕ пД┘ёпГ┘Ѓ┘Ё 26 ┘і┘ѕ┘є┘і┘ѕ 1879 - 7 ┘і┘єпД┘іп▒ 1892 пД┘ёп«п»┘і┘ѕ┘і пЦп│┘ЁпДп╣┘і┘ё пД┘ёп«п»┘і┘ѕ┘і п╣пепДп│ пГ┘ё┘Ё┘і пД┘ёпФпД┘є┘і ┘Ёп╣┘ё┘ѕ┘ЁпДпф п┤п«пх┘іпЕ пД┘ё┘Ё┘і┘ёпДп» 15 ┘є┘ѕ┘Ђ┘Ёпеп▒ 1852пД┘ё┘ѓпД┘Єп▒пЕпї пД┘ёп»┘ѕ┘ёпЕ пД┘ёп╣пФ┘ЁпД┘є┘іпЕ пД┘ё┘ѕ┘ЂпДпЕ 7 ┘і┘єпД┘іп▒ 1892 (39 п│┘єпЕ)пГ┘ё┘ѕпД┘єпї пД┘ёп«п»┘і┘ѕ┘іпЕ пД┘ё┘Ёпхп▒┘іпЕ ┘Ё┘ѕпДпи┘єпЕ пД┘ёп»┘ѕ┘ёпЕ пД┘ёп╣пФ┘ЁпД┘є┘іпЕ пД┘ёп▓┘ѕпгпЕ пБ┘Ё┘і┘єпЕ пЦ┘ё┘Є№┐й...

WRB, 4th edition (2022) World Reference Base for Soil Resources (Pangkalan Rujukan Sumberdaya Tanah Dunia, dikenal dengan singkatannya WRB) adalah sistem klasifikasi tanah baku internasional yang disarankan oleh Badan Ilmu-ilmu Tanah Internasional (International Union of Soil Sciences, IUSS), suatu lembaga di bawah Organisasi Pangan dan Pertanian Dunia (FAO). Pengembangan sistem ini dikoordinasi oleh International Soil Reference and Information Centre (ISRIC) dan ditaja oleh IUSS dan FAO mela...

ТГцућЪУђЁС╝аУ«░ТЮАуЏ«жюђУдЂУАЦтЁЁТЏ┤тцџтЈ»СЙЏТЪЦУГЅуџёТЮЦТ║љсђѓ (2020т╣┤9Тюѕ20ТЌЦ)У»итЇЈтіЕУБютЁЁтЈ»жЮаТЮЦТ║љ№╝їТЌаТ│ЋТЪЦУ»ЂуџётюеСИќС║║уЅЕтєЁт«╣т░єУбФуФІтЇ│уД╗жЎцсђѓ жЎ│жџеТёЈућиТГїТЅІТўхуД░жџеТёЈуИйжІфтИФТГїујІтЏйу▒Ї СИГУЈ»Т░ЉтюІтЄ║ућЪ (1975-12-14) 1975т╣┤12Тюѕ14ТЌЦ№╝ѕ48ТГ▓№╝Ѕ УЄ║уЂБтй░тїќуИБудЈУѕѕжёЅС║їТИ»ТЮЉУЂїСИџТГїТЅІсђЂт╗џтИФсђЂТ╝ћтЊАУ»ГУеђтюІУфъсђЂтЈ░УфъТЋЎУѓ▓уеІт║джФўУЂиТ»ЇТаАтюІуФІуДђТ░┤жФўтиЦУБйтюќуДЉжЁЇтЂХУгЮт«ютљЏтё┐тЦ│СИђтЁњСИђтЦ│жЪ│С╣љу▒╗тъІтЈ░УфъТхЂУАїжЪ│ТеѓтЄ║жЂЊСйютЊЂ№┐й...

тЁДС╝ХС╗Ѓт│ХтЙъСИІуЎйТ│Цую║ТюЏтЁДС╝ХС╗Ѓт│Хтю░уљєСйЇуй« СИГтЏйт╗БТЮ▒уюЂТи▒тю│тИѓтЇЌт▒▒тЇђУхцуЂБтЈіУЏЄтЈБС╣ІУЦ┐тЇЌтЮљТаЄ22┬░24Рђ▓46Рђ│N 113┬░48Рђ▓10Рђ│E / 22.4129┬░N 113.8027┬░E / 22.4129; 113.8027жЮбуЕЇ4.84т╣│Тќ╣тЁгжЄї№╝ѕ2т╣│Тќ╣УІ▒жЄї№╝ЅТюђжФўТхиТІћ338у▒│№╝ѕ1,109УІ▒т░║№╝ЅТюђжФўж╗ът░ќт│░т▒▒у«АУйё СИГтЏйтѕєтЇђт╗БТЮ▒уюЂТи▒тю│тИѓтЇЌт▒▒тЇђ№╝ѕтјЪт▒гт╗БТЮ▒уюЂуЈаТхитИѓждЎТ┤▓тЇђ№╝Ѕ тЁДС╝ХС╗Ѓт│ХуџёжИдуЅЄУѕ╣№╝ї1824т╣┤ тЙъжЮњт▒▒ую║ТюЏтЁДС╝ХС╗Ѓт│Х Тќ░т«ЅуИБтю░тюќ№╝їтЈ»УдІ...

United States Army Medal of Honor recipient Donald R. LobaughDonald Lobaugh in 1942Born(1925-02-07)February 7, 1925Freeport, Pennsylvania, USDiedJuly 22, 1944(1944-07-22) (aged 19)near Afua, Dutch New GuineaPlace of burialRimersburg Cemetery, Rimersburg, PennsylvaniaAllegianceUnited StatesService/branchUnited States ArmyYears of service1942 - 1944RankPrivateUnit127th Infantry Regiment, 32nd Infantry DivisionBattles/warsWorld War IIAwardsMedal of Honor Donald Ronald Lobaugh (February...

Le miracle ├Еconomique japonais est le nom donn├Е ├а la forte expansion ├Еconomique du Japon dans les d├Еcennies qui suivent la Seconde Guerre mondiale. Ruin├Е apr├еs sa capitulation, le pays devient d├еs la fin des ann├Еes 1960 la deuxi├еme puissance ├Еconomique mondiale. La croissance ne prend fin qu'avec l'├Еclatement de la bulle immobili├еre et financi├еre au d├Еbut des ann├Еes 1990. Apr├еs-guerre Parade militaire de l'arm├Еe am├Еricaine sur la place du palais imp├Еrial ├а Tokyo, le 5 jui...
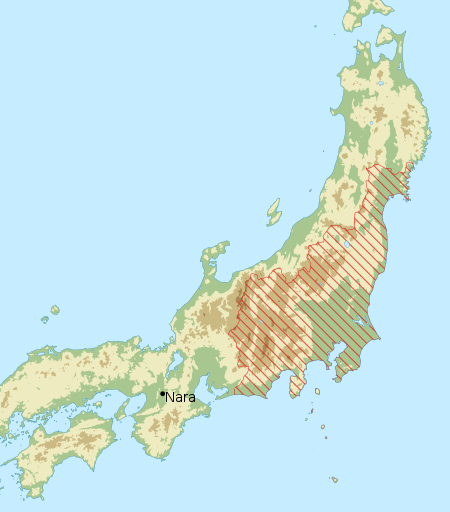
Oldest attested stage of the Japanese language Old JapaneseСИіС╗БТЌЦТюгУфъRubbing of Bussokuseki-kahi poems carved c. 752, recording Old Japanese using Chinese charactersRegionJapanEra8th centuryLanguage familyJaponic Old JapaneseEarly formProto-Japonic Writing systemMan'y┼ЇganaLanguage codesISO 639-3ojpLinguist Listojp [a]Glottologoldj1239This article contains IPA phonetic symbols. Without proper rendering support, you may see question marks, boxes, or other symbols instead of ...

































