מאורת הדרקון (סדרת משחקים)

מאורת הדרקון
Dragon's Lair
כללי
סוגה פנטזיה, אנימציה, משחק הרפתקאות ממוחשב
פיתוח RDI Video Systems, Software Projects, Motivetime, Elite Systems, Sullivan Bluth Studios, Don Bluth Interactive, Dragonstone Software
הוצאה לאור Cinematronics, CSG Imagesoft, Leland Corporation, Data East, Ubisoft, Digital Leisure

מאורת הדרקון (באנגלית: Dragon's Lair) הוא סדרת משחקי וידאו שנוצרו על ידי ריק דייר (אנ').

המשחק הראשון בסדרה פותח במקור כמכונת ארקייד על ידי חברת Cinematronics ויצא במקור לאולמות הארקייד במהלך 1983.[1][2] המשחק היה מבוסס על טכנולוגיית לייזר דיסק, והכיל גרפיקה יוצאת דופן בהשוואה למשחקי וידאו אחרים שיצאו לשווקים באותה התקופה.[3] לאורך השנים פותחו גרסאות שונות של המשחק למספר פלטפורמות אחרות, אף על פי כן, מכיוון שבאותה התקופה שום טכנולוגיה שהייתה זמינה לשימוש ביתי לא יכלה להכיל תוכן באיכות של סרטי לייזרדיסק, יצאו בפועל גרסאות עם תוכן באיכות נמוכה בהרבה לפלטפורמות האחרות.[4] משחק ההמשך "Dragon's Lair II: Time Warp" פותח עוד במהלך 1984 אך יצא לאולמות הארקייד רק ב-1991. בעוד שהגרפיקה של משחק ההמשך זכתה לשבחים, האינטראקטיביות שלו הייתה מיושנת בהשוואה לדור החדש של משחקי הארקייד ובשל כך הוא לא הצליח להפוך לפופולרי כמו המשחק המקורי בזיכיון.

שני המשחקים המרכזיים בזיכיון נחשבים למשחקים קלאסיים[5] אשר זוכים לעיתים רבות לגרסאות מחודשות בדורות החדשים של קונסולות המשחקים.[6]

בעקבות ההצלחה של המשחקים נוצרה גם סדרת אנימציה של "מאורת הדרקון" ששודרה במקור ברשת ABC בשנת 1984 וכמו כן הופקה גם סדרת קומיקס של "מאורת הדרקון" שפורסמה במקור בשנת 2003.

בשנת 1989 רנדי לינדן יצר גרסת המשחק מתאימה למחשבי Amiga.

המשחקים בזיכיון

  • Dragon's Lair(אנ') - (1983;‏ ארקייד, 3DO, Jaguar, CD-i, DOS, Windows, Macintosh, Nintendo DS, Nintendo DSi, PlayStation 3, PSP, SEGA CD, Xbox 360, Android, iOS)
  • Dragon's Lair II: Escape from Singe's Castle‏(אנ') (1987;‏ Amiga, Atari ST, Commodore 64, DOS, ZX Spectrum)
  • Dragon's Lair II: TimeWarp‏(אנ') (1990;‏ Amiga, Atari ST, Macintosh, DOS, Windows)
  • Dragon's Lair III: The Curse of Mordread‏(אנ') (1992;‏ Amiga, Atari ST, DOS)
  • Dragon's Lair 3D: Return to the Lair‏(אנ') (2002;‏ PlayStation 2, GameCube, Windows, Xbox)

משחקיות

במשחקים השחקן מסוגלים לשלוט על ארבעה לחצנים - למעלה, למטה, שמאלה, ימינה ולחצן ההתקפה. במהלך המשחק השחקן צריך להגיב להנחיות שמופיעות על המסך אשר בתגובה מציגים את סצנת האנימציה הבאה במשחק או את סצנת האנימציה שמוצגת כאשר השחקן נהרג והמשחק נגמר. כאשר משחקים בכל אחד מהמשחקים בזיכיון מבלי למות המשחק אמור להימשך בסביבות 12 דקות בלבד. בסך הכל כל המשחקים בזיכיון מכילים בסביבות 22 דקות של תוכן, אשר הם 50,000 פריימים של אנימציה שהופקה מבעוד מועד,[7] כולל מספר סצנות בהם הגיבור נהרג, ומספר סצנת המוצגות בתרחיש בו המשחק מסתיים מבעוד מועד.[8]

הדמויות הראשיות

  • דירק הנועז - הגיבור הראשי בסדרת המשחקים. דירק הוא אביר, אשר לובש שריון וחמוש בחרב, והוא האדם היחיד שמסוגל להציל את הנסיכה דפני מהדרקון האימתני סינג. במשחקים דירק צריך להתמודד עם אתגרים מסוכנים רבים. בשני המשחקים הראשונים מדובב את הדמות דן מולינה.
  • הנסיכה דפני - הדרקון סינג נוהג לחטוף את הנסיכה דפני ודירק הנועז נאלץ תמיד להציל את הנסיכה.
  • סינג הדרקון - אנטגוניסט הראשי בסדרת המשחקים שחוטף את הנסיכה דפני.

מדיות נוספות בזיכיון

סדרת טלוויזיה

בעקבות ההצלחה של המשחק הראשון בזיכיון נוצרה בהמשך סדרת טלוויזיה מצוירת המבוססת על עלילת המשחק שכללה 13 פרקים בני חצי שעה. הסדרה שודרה במקור ברשת ABC מ-8 בספטמבר 1984 עד 27 באפריל 1985.

סדרת קומיקס

בשנת 2003 חברת CrossGen הפיקה ופרסמה סדרת קומיקס המבוססת על המשחק אשר שילבה גם אלמנטים מהעיבוד הטלוויזיוני של המשחק.

קישורים חיצוניים

ויקישיתוף מדיה וקבצים בנושא מאורת הדרקון בוויקישיתוף

הערות שוליים

  1. ^ טל פרוסט.., ביקורטרו: Dragon's Lair, באתר ynet, 1 בינואר 2012
  2. ^ "Review: 'Dragon's Lair' returns on Blu-ray Disc". CNN.com. 18 במאי 2007. נבדק ב-15 במרץ 2016. {{cite web}}: (עזרה)
  3. ^ "Enter The Dragon's Lair" (PDF). Games Magazine. בפברואר 2008. נבדק ב-29 באוקטובר 2018. {{cite news}}: (עזרה)
  4. ^ "Conversion Capers" (PDF). Retro Gamer. במאי 2007. נבדק ב-20 באוקטובר 2018. {{cite news}}: (עזרה)
  5. ^ Service, Marc Saltzman Gannett News. "CNN.com - New 'Dragon's Lair' disappoints - Feb 13, 2003". edition.cnn.com. נבדק ב-29 באוקטובר 2018. {{cite web}}: (עזרה)
  6. ^ Harris, Craig (27 באוקטובר 2010). "Dragon's Lair Trilogy Review". IGN (באנגלית אמריקאית). נבדק ב-29 באוקטובר 2018. {{cite web}}: (עזרה)
  7. ^ [1]
  8. ^ "Dragon's Lair". Animator's Newsletter (8): 39. Spring 1984. נבדק ב-2 במאי 2022. {{cite journal}}: (עזרה)

Read other articles:

The Moon (song)

2000 single by Taxi This article is about the Taxi song. For other songs, see Moon (disambiguation) § Songs. The MoonSingle by TaxiB-sideLunaReleased2000Length2:58LabelIntercontSongwriter(s)Dan TeodorescuProducer(s)TeodorescuTaxi singles chronology Aici sunt banii dumneavoastră (2000) The Moon (2000) Doi zero zero zero (2000) Eurovision Song Contest 2000 entryCountryRomaniaArtist(s) Dan Teodorescu Georgiana Pană Lucian Cioargă Adrian Borțun George Pătrănoiu AsTaxiLanguageEngli...

 

العلاقات السويسرية الكورية الشمالية

العلاقات السويسرية الكورية الشمالية سويسرا كوريا الشمالية   سويسرا   كوريا الشمالية تعديل مصدري - تعديل   العلاقات السويسرية الكورية الشمالية هي العلاقات الثنائية التي تجمع بين سويسرا وكوريا الشمالية.[1][2][3][4][5] مقارنة بين البلدين هذه مقا�...

 

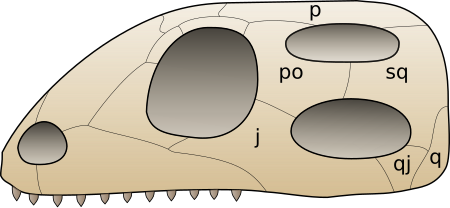
Diapsida

Diapsida Periode Pennsylvanian–Sekarang, 307–0 jtyl PreЄ Є O S D C P T J K Pg N TaksonomiKerajaanAnimaliaFilumChordataKelasReptiliaTanpa nilaiDiapsida Osborn, 1903 Subkelompok †Dolerosaurus †Araeoscelidia Neodiapsida pelbagai klad punah Sauria lbs Diapsida (dua lengkungan) adalah kelompok tetrapoda amniota yang mengembangkan dua lubang (fenestra temporal) di setiap sisi tengkoraknya sekitar 300 juta tahun yang lalu saat periode Karbon Akhir.[1] Diapsida beragam seca...

عنجارة

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) عنجارة الاسم الرسمي عنجارة الإحداثيات 36°13′2″N 36°56′47″E / 36.21722°N 36.94639°E / 36.21722; 36.94639 تقسيم إدا�...

 

Marija Gimbutas

Marija Gimbutas by Kerbstone 52, at the back of Newgrange, Co. Meath, Ireland, in September 1989. Marija Gimbutas (terlahir sebagai Marija Birutė Alseikaitė) (Vilnius, Lituania 23 Januari 1921 – Los Angeles, Amerika Serikat, 2 Februari 1994) adalah seorang arkeolog Amerika Serikat yang asalnya dari Lituania. Ia terutama meneliti kebudayaan Zaman Batu Baru dan Zaman Perunggu dari Eropa Lama, sebuah istilah yang ia perkenalkan. Karya-karya yang diterbitkan antara tahun 1946 dan 1971 memperk...

 

Langouet

Langouet L'église Saint-Armel. Administration Pays France Région Bretagne Département Ille-et-Vilaine Arrondissement Rennes Intercommunalité Communauté de communes du Val d'Ille-Aubigné Maire Mandat Jean-Luc Dubois 2020-2026 Code postal 35630 Code commune 35146 Démographie Gentilé Langouëtiens Populationmunicipale 617 hab. (2021 ) Densité 88 hab./km2 Population agglomération 18 579 hab. Géographie Coordonnées 48° 14′ 59″ nord, 1° 49�...

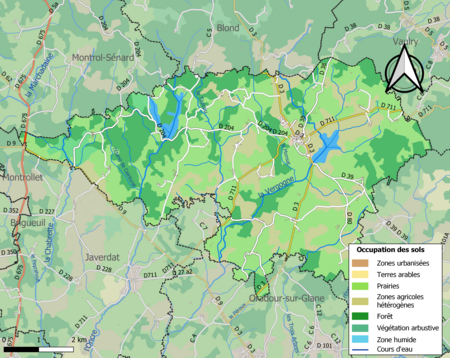
Cieux

Peta infrastruktur dan tata guna lahan di Komune Cieux.  = Kawasan perkotaan  = Lahan subur  = Padang rumput  = Lahan pertanaman campuran  = Hutan  = Vegetasi perdu  = Lahan basah  = Anak sungaiCieux merupakan sebuah komune di departemen Haute-Vienne di Prancis. Lihat pula Komune di departemen Haute-Vienne Referensi INSEE lbsKomune di departemen Haute-Vienne Aixe-sur-Vienne Ambazac Arnac-la-Poste Augne Aureil Azat-le-Ris Balledent La Bazeuge Beaumont-du...

 

Dražen Petrović

Yugoslav-Croatian basketball player (1964–1993) Dražen PetrovićPetrović with the New Jersey Nets in 1992Personal informationBorn(1964-10-22)22 October 1964Šibenik, Croatia, YugoslaviaDied7 June 1993(1993-06-07) (aged 28)Denkendorf, GermanyNationalityCroatianListed height6 ft 5 in (1.96 m)Listed weight195 lb (88 kg)Career informationNBA draft1986: 3rd round, 60th overall pickSelected by the Portland Trail BlazersPlaying career1979–1993PositionShooting guar...

 

Very Large Telescope

Very Large TelescopeNama alternatifVLT Bagian dariObservatorium Paranal LokasiRegion Antofagasta, ChiliKoordinat24°37′38″S 70°24′15″W / 24.62733°S 70.40417°W / -24.62733; -70.40417Koordinat: 24°37′38″S 70°24′15″W / 24.62733°S 70.40417°W / -24.62733; -70.40417 OrganisasiObservatorium Selatan Eropa Ketinggian2.635 m (8.645 ft) Waktu pengamatan320 Panjang gelombang300 nm – 20 μm (visible, nea...

2020年夏季奧林匹克運動會波蘭代表團

2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl（英文）（波兰文）2020年夏季奥林匹克运动会（東京）2021年7月23日至8月8日（受2019冠状病毒病疫情影响推迟，但仍保留原定名称）運動員206參賽項目24个大项旗手开幕式：帕维尔·科热尼奥夫斯基（游泳）和马娅·沃什乔夫斯卡（自行车）[1]闭幕式：卡罗利娜·纳亚（皮划艇）&#...

 

العلاقات الجزائرية الفيتنامية

العلاقات الجزائرية الفيتنامية الجزائر فيتنام   الجزائر   فيتنام تعديل مصدري - تعديل   العلاقات الجزائرية الفيتنامية هي العلاقات الثنائية التي تجمع بين الجزائر وفيتنام.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه الم...

 

Dall's porpoise

Species of porpoise endemic to the North Pacific Dall's porpoise[1] Size compared to an average human Conservation status Least Concern  (IUCN 3.1)[2] CITES Appendix II (CITES)[3] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Artiodactyla Infraorder: Cetacea Family: Phocoenidae Genus: Phocoenoides(Andrews, 1911) Species: P. dalli Binomial name Phocoenoides dalli(True, 1885)   Dall's porpoi...

Johnson & Johnson

American multinational pharmaceutical and consumer goods corporation Not to be confused with S. C. Johnson & Son. J&J redirects here. For other uses, see J & J (disambiguation). Johnson & JohnsonHeadquarters at One Johnson and Johnson Plaza in New Brunswick, New Jersey, U.S.Company typePublicTraded asNYSE: JNJDJIA componentS&P 100 componentS&P 500 componentISINUS4781601046IndustryPharmaceuticalMedical TechnologyFoundedJanuary 1886; 138 years ago&...

 

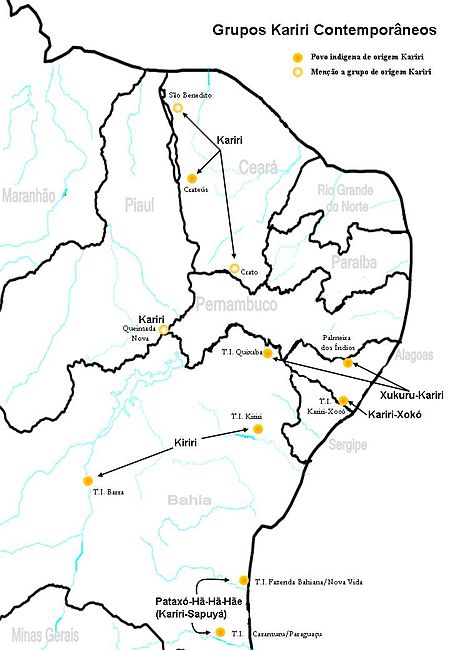
Kariri languages

Extinct Macro-Ge dialect cluster of Brazil KariríKaririanNative toBrazilRegionbetween Bahia and MaranhãoEthnicityKiriri peopleExtinctca. 1970Language familyMacro-Gê KariríLanguage codesISO 639-3kzwGlottologkari1254  Kariri The Karirí languages, generally considered dialects of a single language, were a group of languages formerly spoken by the Kiriri people of Brazil. It was spoken until the middle of the 20th century; the 4,000 ethnic Kiriri are now monolingual Portuguese spea...

 

Michigan's 8th congressional district

U.S. House district for Michigan Michigan's 8th congressional districtInteractive map of district boundaries since January 3, 2023Representative  Dan KildeeD–Flint TownshipPopulation (2022)768,166Median householdincome$57,526[1]Ethnicity73.4% White14.9% Black5.4% Hispanic4.6% Two or more races1.1% Asian0.7% otherCook PVIR+1[2] Michigan's 8th congressional district is a United States congressional district in Central Michigan. The district was first created in 1873, afte...

Embalming (manga)

Japanese manga series Not to be confused with The Embalmer (manga). Embalming: The Another Tale of FrankensteinFirst tankōbon volume coverエンバーミング –THE ANOTHER TALE OF FRANKENSTEIN–(Enbāmingu Ji Anazā Teiru obu Furankenshutain)GenreAction[1]Dark fantasy[2] MangaEmbalming: Dead Body and BrideWritten byNobuhiro WatsukiPublished byShueishaEnglish publisherNA: Viz MediaMagazineJump the Revolution!DemographicShōnenPublishedSeptember 30, 2005 MangaEmba...

 

Académie royale de peinture et de sculpture

Sebuah pertemuan Académie Royale de Peinture et de Sculpture di Istana Louvre (skt. 1712-21) oleh Jean-Baptiste Martin Académie Royale de Peinture et de Sculpture (bahasa Prancis: [akademi ʁwajal də pɛ̃tyʁ e də skyltyʁ]; bahasa Inggris: Royal Academy of Painting and Sculpture) merupakan sebuah akademi yang didirikan pada 1648 di Paris, Prancis. Lembaga ini merupakan lembaga seni rupa utama Prancis pada tahap akhir Rezim Ancien hingga dihapuskan pada 1793 selama Revolusi Pran...

 

寒帯

  fa fb fc fd m wa wb wc wd sa sb sc sd   E 寒帯   ET EF D 亜寒帯 Dfa Dfb Dfc Dfd Dwa Dwb Dwc Dwd Dsa Dsb Dsc Dsd   C 温帯 Cfa Cfb Cfc   Cwa Cwb Cwc Csa Csb Csc   B 乾燥帯   BSh BSk BWh BWk A 熱帯 Af   Am Aw   As   寒帯（かんたい）とは、気候帯の一種で最暖月平均気温が10℃未満の地域である（降水量は無条件）。この地域では樹木の生育は基本的に不可能である。 ケッペン...

Championnat d'Asie féminin de basket-ball des moins de 16 ans

Cet article traite de l'épreuve féminine. Pour la compétition masculine, voir Championnat d'Asie masculin de basket-ball des moins de 16 ans. Championnat d'Asie féminin de basket-ball des moins de 16 ans Généralités Sport Basket-ball Création 2009 Organisateur(s) FIBA Asie Éditions 7 (en 2023) Catégorie Moins de 16 ans Périodicité Bisannuelle Participants Division A : 9 équipesDivision B : 8 équipes Palmarès Tenant du titre Australie Plus titré(s) Australie Chine (3...

 

Noether's theorem

Statement relating differentiable symmetries to conserved quantities This article is about Emmy Noether's first theorem, which derives conserved quantities from symmetries. For other uses, see Noether's theorem (disambiguation). First page of Emmy Noether's article Invariante Variationsprobleme (1918), where she proved her theorem Part of a series of articles aboutCalculus ∫ a b f ′ ( t ) d t = f ( b ) − f ( a ) {\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)} Fundamental...