חבורה אוליגומורפית
|
Read other articles:

Huta BolonDesaKantor Kepala Desa Huta BolonNegara IndonesiaProvinsiSumatera UtaraKabupatenSamosirKecamatanPangururanKode pos22392Kode Kemendagri12.17.08.2009 Luas... km2Jumlah penduduk... jiwaKepadatan... jiwa/km2 Huta Bolon adalah salah satu desa yang berada di Kecamatan Pangururan, Kabupaten Samosir, Provinsi Sumatera Utara, Indonesia. Galeri Gapura Selamat Datang di Desa Huta Bolon Pemukiman masyarakat di Desa Huta Bolon Gereja HKBP Parbaba Pantai Pasir Putih Parbaba di Desa Huta Bolo...

Logo APCYS 2021 Asia Pacific Conference of Young Scientists (Konferensi Asia Pasifik Ilmuwan Muda) atau yang biasa disingkat dengan APCYS adalah sebuah konferensi ilmiah tahunan bagi para siswa/I sekolah tingkat menengah se‐ Asia Pasifik sebagai ajang untuk menumbuhkan iklim penelitian di kalangan generasi muda. APCYS pertama kali diselenggarakan pada tanggal 2 - 7 September 2012, berlokasi di Swiss- Belhotel Danum Palangka Raya,[1] Kalimantan Tengah. Acara ini akan dibuka oleh Waki...

1957 novel by Allen Adler Mach 1: A Story of Planet Ionus Cover of Terror on Planet IonusAuthorAllen A. AdlerCountryUnited KingdomLanguageEnglishGenreScience fiction novelPublisherFarrar, Straus and CudahyPublication date1957Media typePrint (Hardcover)Pages212 pp Mach 1: A Story of Planet Ionus is a 1957 science fiction novel by Allen A. Adler. A paperback version was published in 1966 by Paperback Library with the alternate title Terror on Planet Ionus. Synopsis While testing an experim...

S-36 Role Eight-seat amphibianType of aircraft National origin United States Manufacturer Sikorsky Aircraft First flight 1927 Introduction 1927 Primary user Pan American Airways Number built 6 Developed from Sikorsky S-34 Developed into Sikorsky S-38 The Sikorsky S-36 was an eight-seat amphibian sesquiplane designed and built by the Sikorsky Manufacturing Company in the late 1920s. The aircraft was ordered by Pan American Airways, the start of a long association with Sikorsky flying boa...

Supreme Court of the United States38°53′26″N 77°00′16″W / 38.89056°N 77.00444°W / 38.89056; -77.00444EstablishedMarch 4, 1789; 235 years ago (1789-03-04)LocationWashington, D.C.Coordinates38°53′26″N 77°00′16″W / 38.89056°N 77.00444°W / 38.89056; -77.00444Composition methodPresidential nomination with Senate confirmationAuthorized byConstitution of the United States, Art. III, § 1Judge term lengthl...

Study of Mary in Catholic theology The Blessed Virgin Mary is depicted in a rose-garden with angels playing music. Roses are a symbol of Mary. Part of a series on theMariologyof the Catholic ChurchImmaculate Conception by Bartolomé Esteban Murillo (c. 1675) Overview Prayers Antiphons Titles Hymns to Mary Devotional practices Saints Societies Consecrations and entrustments Veneration Titles of Mary Theotokos (Mother of God) Mediatrix Mother of the Church Our Lady of Good Counsel Our Lad...

American college basketball season 2022–23 San Francisco Dons men's basketballHall of Fame Classic championsConferenceWest Coast ConferenceRecord20–14 (7–9 WCC)Head coachChris Gerlufsen (1st season)Assistant coaches Michael Plank Jay Duncan Kyle Bankhead Home arenaWar Memorial Gymnasium(Capacity: 3,005)Seasons← 2021–222023–24 → 2022–23 West Coast Conference men's basketball standings vte Conf Overall Team W L PCT W L PCT ...

2003 single by Kelly Clarkson LowSingle by Kelly Clarksonfrom the album Thankful ReleasedAugust 3, 2003 (2003-08-03)GenrePopLength3:28LabelRCASongwriter(s)Jimmy HarryProducer(s)Clif MagnessKelly Clarkson singles chronology Miss Independent (2003) Low (2003) The Trouble with Love Is (2003) Music videoLow on YouTube Low is a song by American singer-songwriter Kelly Clarkson from her debut album, Thankful (2003). The song was written by Jimmy Harry and produced by Clif Magness. It...

Tris Speaker is the all-time leader in doubles, with 792. In baseball, a double is a hit in which the batter advances to second base in one play, without the benefit of a fielding error, advancing to second on a throw to another base, or another runner being put out on a fielder's choice.[1] A batter may also be credited with a ground-rule double when a fair ball, after touching the ground, bounds into the stands or becomes lodged in a fence or scoreboard.[2] Hall of Fame cen...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Not to be confused with the Anne, a sloop captured during 19th-century West Indies anti-piracy operations. Annie Annie History United States OwnerMystic Seaport BuilderDavid O. Richmond Completed1880 StatusMuseum ship General characteristics Length28 ft (8.5 m)[1] PropulsionSail Sail planSandbagger sloop Annie is a Sandbagger sloop located at Mystic Seaport in Mystic, Connecticut, United States. Built in 1880 in Mystic by David O. Richmond, Annie was built for Henry H. Tift ...

Nogometni klub TolminCalcio Tminci Segni distintiviUniformi di gara Casa Trasferta Colori socialiRosso e nero InnoRdeče-črni iz Tolmina, naj se piše zgodovinaLeon Oblak Dati societariCittàTolmino Nazione Slovenia ConfederazioneUEFA Federazione NZS Fondazione1921 Presidente Mitja Taljat Allenatore Sanel Konjević StadioŠportni park Brajda(500 posti) Sito webhttps://www.nktolmin.si/ PalmarèsSi invita a seguire il modello di voce NK Tolmin 2019-2020 Il Nogometni klub Tolmin, noto come...

Primary alcohol Luche reduction Named after Jean-Louis Luche Reaction type Organic redox reaction Identifiers Organic Chemistry Portal luche-reduction RSC ontology ID RXNO:0000286 Luche reduction is the selective organic reduction of α,β-unsaturated ketones to allylic alcohols.[1][2][3] The active reductant is described as cerium borohydride, which is generated in situ from NaBH4 and CeCl3(H2O)7.[4] The Luche reduction can be conducted chemoselectively toward...

Ethnic group Mongolians in the United KingdomTotal populationMongolian-born residents293 (2001 UK Census)1,689 (2011 UK Census)Other population estimates5,000–7,000 (2009 community leaders' estimates)Regions with significant populationsGreater London, ManchesterLanguagesMongolian, British EnglishReligionTibetan Buddhism Part of a series onBritish people United Kingdom Cornish English Gaelic Manx Northern Irish Orcadian Scottish Welsh Eastern European Albanian Belarusian Bulgarian Czech Hung...

Ongoing COVID-19 viral pandemic in Kazakhstan COVID-19 pandemic in KazakhstanDiseaseCOVID-19Virus strainSARS-CoV-2LocationKazakhstanFirst outbreakWuhan, Hubei, ChinaIndex caseAlmatyArrival date13 March 2020(4 years, 3 months and 2 days)Confirmed cases1,231,856[1][2]Recovered1,067,201[1]Deaths13,134[1]Government websitewww.coronavirus2020.kz/kz The COVID-19 pandemic in Kazakhstan was a part of the worldwide pandemic of coronavirus disease 2019 (CO...
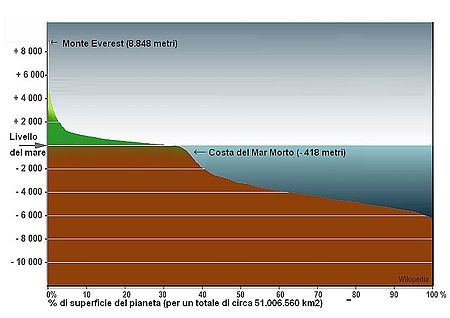
Questa pagina sull'argomento geografia sembra trattare argomenti unificabili alla pagina Quota ortometrica. Puoi contribuire unendo i contenuti in una pagina unica. Segui i suggerimenti del progetto di riferimento. Questa voce o sezione sugli argomenti aviazione e geografia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti dei pro...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2022) اتحاد المقعدين اللبنانيين اتحاد المقعدين اللبنانيين المقر الرئيسي لبنان تاريخ التأسيس 1981 الموقع الرسمي الموقع الرسمي تعديل مصدري - تعديل ات�...

مقاطعة هرسين الإحداثيات 34°20′00″N 47°30′00″E / 34.333333333333°N 47.5°E / 34.333333333333; 47.5 [1] تقسيم إداري البلد إيران[2] التقسيم الأعلى كرمانشاه[3] العاصمة هرسين عدد السكان عدد السكان 78350 (2016)[3] عدد الأسر 22506 (2016)[3] معلومات أخرى منطق...

الدوري العراقي الممتاز السلسلة دوري نجوم العراق الموسم 1982–83 البلد العراق الفرق 12 الفائز صلاح الدين(اللقب الأول) هداف الدوري حسين سعيد(17 هدف) 1981–82 1983–84 تعديل مصدري - تعديل دوري أندية العراق للدرجة الأولى 1982–83 هي الموسم التاسع من الدوري العراقي الممتاز منذ ت�...

Pour les articles homonymes, voir Latin (homonymie). Ne doit pas être confondu avec Musique latino-américaine. Musique latine est un terme utilisé par l'industrie musicale pour classer les différents styles musicaux de l'Amérique ibérique[1], qui englobe l'Amérique latine, l'Espagne, le Portugal et la population latino du Canada et des États-Unis[2], ainsi que la musique chantée en espagnol et en portugais[3],[4],[5],[6],[7],[8],[9],[10]. Terminologie Parce que la majorité des immi...



















































































