זרם העתקה
|
Read other articles:

Tenda Ramadan adalah sebuah tempat yang didirikan pada bulan Ramadan dan dipakai untuk berbuka puasa. Hal tersebut pertama kali terjadi di Kairo, Mesir dan kemudian menyebar ke daerah Arab dan dikembangkan sebagai destinasi khusus saat bulan Ramadan. Pada awalnya, tenda tersebut dibangun sebagai tempat belasungkawa yang dikenal sebagai Saradek dalam bahasa Arab. Selain itu, tempat tersebut juga digunakan sebagai tempat yang menyediakan makanan atau keperluan untuk orang yang membutuhkan. Nam...

Untuk kegunaan lain, lihat PAL. Sebuah pal yang menunjukkan titik nol Kecamatan Banyuwangi, Kabupaten Banyuwangi, Jawa Timur. Pal[1] atau tonggak penanda jarak (Inggris: milestone) adalah rangkaian tonggak yang dipasang di median atau pinggir jalan maupun rel kereta api untuk menunjukkan seberapa jauh suatu ruas jalan/rel telah ditempuh. Pal umumnya berbentuk batu yang dilengkapi penanda angka jarak tempuh beserta penanda nama daerah yang diukur. Pal dipasang antara satu tonggak d...

German physician and astrologer (1505–1577) Achilles GasserBorn(1505-11-03)3 November 1505Lindau, Holy Roman EmpireDied4 December 1577(1577-12-04) (aged 72)Mixed Imperial City of Augsburg, Holy Roman EmpireKnown forComet observations, research on European history and geographyScientific careerFieldsAstronomycartography Achilles Pirmin Gasser[1] (3 November 1505 – 4 December 1577)[2] was a German physician and astrologer. He is now known as a well-connected human...

Pour les articles homonymes, voir Ordre du Mérite. Ordre du Mérite Grand cordon de l'ordre du Mérite. Ordre du Mérite Conditions Décerné par Liban Type Ordre honorifique civil comportant 6 classes Décerné pour Services rendus à l'état Libanais Éligibilité Militaires ou civils Détails Statut Toujours décerné Grades Grade extraordinaireGrand cordon1re classe2e classe3e classe4e classe Statistiques Création 16 janvier 1922 Ordre de préséance InférieurOrdre national du Cèdre ...

لوي جاك تينار (بالفرنسية: Louis Jacques Thénard) معلومات شخصية الميلاد 4 مايو 1777 [1][2][3] الوفاة 21 يونيو 1857 (80 سنة) [1][2][3] باريس مواطنة فرنسا عضو في الجمعية الملكية، وجمعية محبي العلوم بباريس، وأكاديمية العلوم المفيدة، والأكاديمي�...

Kota San Pablo component city Dinamakan berdasarkanPaulus dari Thebes Tempat Negara berdaulatFilipinaIsland group of the PhilippinesLuzonRegion di FilipinaCalabarzonProvinsi di FilipinaLaguna NegaraFilipina Pembagian administratifVI-D VII-B VII-C VII-D Bagong Bayan Concepcion Del Remedio Dolores San Buenaventura San Crispin San Diego San Francisco San Isidro San Jose San Lorenzo San Lucas 1 San Lucas 2 San Mateo San Pedro Santa Catalina Santa Isabel Santa Veronica Santo Angel PendudukTotal285...

Halaman ini berisi artikel tentang waralaba media. Untuk dunia fiksi bedasarkan Harry Potter, lihat Dunia fiksi Harry Potter. Untuk taman hiburan, lihat The Wizarding World of Harry Potter. Wizarding WorldDiciptakan olehJ. K. RowlingKarya asliHarry Potter and the Philosopher's Stone (2001)PemilikJ. K. Rowling (hak penerbitan dan publikasi)Warner Bros. Entertainment (hak terkait film, TV, permainan)Publikasi tercetakBukuDaftar bukuFilm dan televisiFilm Film Harry Potter Film Fantastic Beasts P...

Questa voce o sezione sull'argomento personaggi dei fumetti non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Kang il Conquistatore UniversoUniverso Marvel Nome orig.Kang the Conqueror Lingua orig.Inglese AutoriStan Lee Jack Kirby EditoreMarvel Comics 1ª app.ottobre 1963 1ª app. inThe Fa...

1933 American filmOld King ColeDirected byDavid HandProduced byWalt DisneyColor processTechnicolorProductioncompanyWalt Disney ProductionsDistributed byUnited ArtistsRelease date July 29, 1933 (1933-07-29) Running time7:15CountryUnited StatesLanguageEnglish Old King Cole is a Disney cartoon in the Silly Symphonies series, based on several nursery rhymes and fairy tales, including Old King Cole. It was directed by David Hand and released on July 29, 1933.[1] It's a semi-...
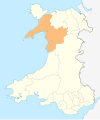
Railway station in Gwynedd, Wales TonfanauGeneral informationLocationTonfanau, GwyneddWalesCoordinates52°36′50″N 4°07′26″W / 52.614°N 4.124°W / 52.614; -4.124Grid referenceSH563038Managed byTransport for WalesPlatforms1Other informationStation codeTNFClassificationDfT category F2Passengers2018/19 3,0582019/20 2,1582020/21 1902021/22 1,1162022/23 1,556 NotesPassenger statistics from the Office of Rail and Road Tonfanau railway station is a railway stop that ...

كأس الدوري البرتغالي 2014–15 تفاصيل الموسم كأس الدوري البرتغالي النسخة 8 البلد البرتغال التاريخ بداية:26 يوليو 2014 نهاية:29 مايو 2015 مباريات ملعوبة 83 عدد المشاركين 36 أهداف مسجلة 200 كأس الدوري البرتغالي 2013–14 كأس الدوري البرتغالي 2015–16 تعديل مصدر...

بطولة تونس للكرة الطائرة للرجال الموسم 1999-1998 البلد تونس المنظم الجامعة التونسية للكرة الطائرة النسخة 44 الفائز الترجي الرياضي التونسي بطولة تونس للكرة الطائرة للرجال 1997-1998 بطولة تونس للكرة الطائرة للرجال 1999-2000 تعديل مصدري - تعديل بطولة تونس للكرة الطائرة للرجال ...

السينما المستقلة هي تسمية أو تعريف للأفلام السينمائية التي يتم إنتاجها خارج منظومة الاستوديوهات، وشركات الإنتاج والتوزيع الكبرى التي تتحكم في هذه الصناعة. تميزت السينما المستقلة في البداية بخروجها عن الخط التجاري الاستهلاكي، كما تميزت بتقديمها محتوى إبداعي أكثر حرية و�...

一中同表,是台灣处理海峡两岸关系问题的一种主張,認為中华人民共和国與中華民國皆是“整個中國”的一部份,二者因為兩岸現狀,在各自领域有完整的管辖权,互不隶属,同时主張,二者合作便可以搁置对“整个中國”的主权的争议,共同承認雙方皆是中國的一部份,在此基礎上走向終極統一。最早是在2004年由台灣大學政治学教授張亞中所提出,希望兩岸由一中各表�...

Pour les articles homonymes, voir Agadir (homonymie). Cet article possède un paronyme, voir Akadyr. Agadir ⴰⴳⴰⴷⵉⵔ أݣادير Héraldique Administration Pays Maroc Région Souss-Massa[1] Préfecture Agadir Ida-Outanane Maire Aziz Akhannouch (2021) Code postal 80000 Démographie Gentilé Gadiri, Gadirie[2]Agadirois, Agadiroise[3] Population 979 248 hab.[4] (2023) Densité 11 422 hab./km2 Population de l'agglomération 1 652 959 hab. (2020) Géo...

Carlos Alberto Informasi pribadiNama lengkap Carlos Alberto Gomes de JesusTanggal lahir 11 Desember 1984 (umur 39)Tempat lahir Rio de Janeiro, BrasilTinggi 1,75 m (5 ft 9 in)Posisi bermain GelandangInformasi klubKlub saat ini Vasco da GamaNomor 10Karier junior2000–2001 FluminenseKarier senior*Tahun Tim Tampil (Gol)2002–2003 Fluminense 43 (5)2004–2005 Porto 22 (2)2005–2007 Corinthians 47 (10)2007 → Fluminense (loan) 5 (1)2007–2010 Werder Bremen 2 (0)2008 → S�...
Menahem Beginמנחם בגין Menahem Begin en 1978. Fonctions Premier ministre d'Israël 21 juin 1977 – 10 octobre 1983(6 ans, 3 mois et 19 jours) Président Ephraïm KatzirYitzhak NavonChaim Herzog Gouvernement Begin I et II Prédécesseur Yitzhak Rabin Successeur Yitzhak Shamir Ministre de la Défense 14 février 1983 – 23 février 1983(9 jours) Président Yitzhak Navon Premier ministre Lui-même Gouvernement Begin II Prédécesseur Ariel Sharon Successeur Moshe A...

南非经济南非經濟首都約翰內斯堡货币蘭特(ZAR)财政年度4月1日 – 3月31日(政府);3月1日 – 2月28/29日(企業及私人)贸易组织世界貿易組織、20國集團、南部非洲關稅聯盟及其他统计数据GDP7309.13亿美元(名义值,2023年估计值) 1.050 万亿美元(购买力平价,2023 年估计值)GDP增长率▲ +2.6% (2012年估計) 人均GDP8,078美元 (2011年) (名義; 71位) 11,035美元 (2011年估計) (購買力平價;...

Type of clock This article is about the type of clock. For the 2009 film, see Timer (film). For the cartoon character, see Time for Timer. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Timer – news · newspapers · books · scholar · JSTOR (February 2024) (Learn how and when to remove this message) A typical ...

Polish comicsEarliest publications1930sPublishersEgmont PolskaTaurus MediaMucha ComicsTimof i Cisi WspólnicyKultura GniewuPublicationsFunky KovalJeż JerzyKapitan ŻbikLil i PutCreatorsTadeusz BaranowskiHenryk ChmielewskiJanusz ChristaSzarlota PawelGrzegorz RosińskiSeriesKoziołek MatołekTytus, Romek i A'TomekOsiedle SwobodaKajko i KokoszLanguagesPolishRelated articlesEuropean comicsCzech comicsHungarian comics ComicsSpeech balloon Comics studies Education Glossary History Methods Cartoon...




















































