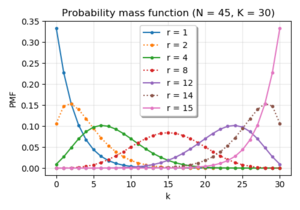
התפלגות היפרגאומטרית שלילית
| ||||||||||||||||||||||||||||||
Read other articles:

Tony George pada 2007 Anton Hulman Tony George (lahir 30 Desember 1959) merupakan seorang pengusaha Amerika Serikat. Ia merupakan cucu dari Tony Hulman. George menjadi Presiden dan CEO dari Indianapolis Motor Speedway dan Hulman & Company dari 1989 sampai 2009. Dibawah pimpinannya, sirkuit Indianapolis tidak hanya menggelar lomba Indianapolis 500 melainkan juga lomba-lomba lainnya diantaranya NASCAR Brickyard 400, Formula Satu Grand Prix Amerika Serikat dan Grand Prix Sepeda Motor Indiana...

WatukosekDesaNegara IndonesiaProvinsiJawa TimurKabupatenPasuruanKecamatanGempolKode pos67155Kode Kemendagri35.14.12.2010 Luas± 374,76 HaJumlah penduduk4.076 (2010) Untuk kegunaan lain, lihat Watu (disambiguasi). Watukosek adalah sebuah desa di Kecamatan Gempol, Kabupaten Pasuruan, Jawa Timur. Secara geografis, Watukosek berbatasan dengan Desa Kebon Agung (Kabupaten Sidoarjo) di utara, Desa Wates (Kabupaten Mojokerto) di barat, Desa Bulusari di selatan, dan Desa Carat di timur. Pada masa...

Салоникский фронт Первой мировой войныОсновной конфликт: Первая мировая война Войска Антанты. Слева направо: солдаты из Индокитая, Франции, Сенегала, Британии, Российской империи, Италии, Сербии, Греции и Индии. Дата 27 октября 1915 — ноябрь 1918 Место Сербия, Черногория, Грец�...

Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. Questa voce o sezione sugli argomenti disturbi psichici e malattie non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Distur...

Questa voce sull'argomento società calcistiche russe è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. FK ŠinnikCalcio šina Segni distintivi Uniformi di gara Casa Trasferta Colori sociali Bianco, nero, azzurro Dati societari Città Jaroslavl' Nazione Russia Confederazione UEFA Federazione RFU Campionato Pervaja Liga Fondazione 1957 Presidente Vladimir Šepel Allenatore Ivan Ljak Stadio Šinnik(26 000 posti) Sito web www.shinnik.yar.ru Palmarès...

Maleakhi 1Seluruh Kitab Maleakhi pada Codex Gigas, yang dibuat sekitar abad ke-13.KitabKitab MaleakhiKategoriNabi-nabi KecilBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen39← Zakharia 14 pasal 2 → Maleakhi 1 (disingkat Mal 1) adalah bagian pertama dari Kitab Maleakhi dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Memuat Firman Allah yang disampaikan dengan perantaraan Maleakhi.[1][2] Teks Naskah aslinya ditulis dalam bahasa Ibrani. Pasa...

Biografi ini memerlukan lebih banyak catatan kaki untuk pemastian. Bantulah untuk menambahkan referensi atau sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus, khususnya jika berpotensi memfitnah.Cari sumber: Muhammad Abduh – berita · surat kabar · buku · cendekiawan · JSTOR (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Muhammad Abduh GelarMuftiInformasi...

Cocktail of vodka and coffee liqueur This article is about a cocktail. For African diaspora in Russia, see Afro-Russian. For other uses, see Black Russian (disambiguation). Black RussianIBA official cocktailA black Russian cocktailTypeCocktailBase spirit Vodka ServedOn the rocks: poured over iceStandard drinkware Old fashioned glassIBA specifiedingredients† 50 ml Vodka 20 ml Coffee liqueur PreparationPour the ingredients into the old fashioned glass filled with ice cubes. Stir gen...

British Baronet, physician and neurologist William Jenner PhysicJenner as caricatured by Spy (Leslie Ward) in Vanity Fair, April 1873 Sir William Jenner, 1st Baronet, GCB, QHP, FRCP, FRS (30 January 1815 – 11 December 1898) was a significant English physician primarily known for having discovered the distinction between typhus and typhoid. Biography Jenner was born at Chatham on 30 January 1815, and educated at University College London. He became a Member of the Royal College ...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

This article is about the German People's Party which existed between 1918 and 1933. For other parties with same name, see German People's Party (disambiguation). Political party in Germany German People's Party Deutsche VolksparteiLeaderGustav StresemannFounded15 December 1918; 105 years ago (15 December 1918)Dissolved4 July 1933; 90 years ago (4 July 1933)Preceded byNational Liberal PartyFree Conservative Party (moderate elements)Merged intoFree Democ...

Glauco Lolli Ghetti Glauco Lolli Ghetti (Ferentino, 31 marzo 1921 – Genova, 18 aprile 2006) è stato un armatore e dirigente sportivo italiano. Indice 1 Biografia 1.1 Attività imprenditoriale 1.2 Attività sportiva 2 Onorificenze 3 Note 4 Altri progetti Biografia Laureato in Chimica farmaceutica all'Università degli Studi di Genova nel 1944, sposò la nipote dell'armatore e senatore Giovanni Battista Bibolini, Maria Amelia. Attività imprenditoriale Fu chiamato nel suo gruppo armatoriale ...

American politician George Bryan Porter3rd Territorial Governor of MichiganIn officeAugust 6, 1831 – July 6, 1834PresidentAndrew JacksonPreceded byLewis CassSucceeded byStevens T. MasonMember of the Pennsylvania House of RepresentativesIn office1827–1827 Personal detailsBorn(1791-02-09)February 9, 1791Norristown, Pennsylvania, U.S.DiedJuly 6, 1834(1834-07-06) (aged 43)Detroit, Michigan, U.S.Resting placeElmwood CemeteryDetroit, MichiganPolitical partyDemocratic partySpouseSa...

List of software application features The Red O-Letter-Logo of the Opera Browser, in use since September 2015.[1] This article details features of the Opera web browser. Currently supported features Access recently closed pages Opera allows its users to retrieve all of the tabs or windows closed earlier in the current session from a list. Closed tabs can be recovered in the reverse sequence in which they were closed, by default this is achieved via the keyboard shortcut Ctrl + Shift +...

みなみく南区 中田島砂丘廃止日 2024年1月1日廃止理由 行政区の再編南区、中区、東区、西区、北区(三方原地区)→中央区現在の行政区 中央区廃止時点のデータ国 日本地方 中部地方、東海地方都道府県 静岡県市 浜松市団体コード 22134-1面積 46.84km2(境界未定部分あり)総人口 98,436人(推計人口、2023年12月1日)隣接自治体隣接行政区 浜松市(東区、西区、中区)磐田�...

指臼岳Вулкан Баранского 指臼岳(2016年)標高 1,125 m所在地 領土問題あり 日本(北海道紗那郡紗那村) ロシア(サハリン州クリル管区)位置 北緯45度5分59秒 東経148度1分11秒 / 北緯45.09972度 東経148.01972度 / 45.09972; 148.01972座標: 北緯45度5分59秒 東経148度1分11秒 / 北緯45.09972度 東経148.01972度 / 45.09972; 148.01972種類 活火山ランク分け対�...

All numbers between two given numbers This article is about intervals of real numbers and some generalizations. For intervals in order theory, see Interval (order theory). For other uses, see Interval (disambiguation). The addition x + a on the number line. All numbers greater than x and less than x + a fall within that open interval. In mathematics, a real interval is the set of all real numbers lying between two fixed endpoints with no gaps. Each endpoint is either a real number or positive...

Voce principale: Associazione Calcio Monza Brianza 1912. Calcio MonzaStagione 1984-1985Sport calcio Squadra Monza Allenatore Alfredo Magni All. in seconda Roberto Gori Presidente Valentino Giambelli Serie B9º Coppa ItaliaPrimo turno Maggiori presenzeCampionato: Saltarelli e Torresin (38) Miglior marcatoreCampionato: Ambu (8) StadioGino Alfonso Sada 1983-1984 1985-1986 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti il Calcio Monza nelle compet...

Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. Legamento crociato anteriore Articolazione del ginocchio vista posteriormente Latino Ligamenta cruciata genus Da Femore A Tibia Il legamento crociato anteriore (in latino ligamenta cruciata genus[1]), noto in ambito medico con l'acronimo LCA o in quello inglese ACL, è uno dei quattro più importa...

Irish politician (born 1978) Ruairí Ó MurchúTDÓ Murchú in 2022Teachta DálaIncumbentAssumed office February 2020ConstituencyLouth Personal detailsBorn (1978-05-03) 3 May 1978 (age 46)Dundalk, County Louth, IrelandPolitical partySinn FéinSpouseAnnemarie Ó MurchúChildren3Alma materDublin City University Ruairí Ó Murchú (Irish pronunciation: [ˈɾˠuəɾʲiː oː ˈmˠʊɾˠəxuː]; born 3 May 1978) is an Irish Sinn Féin politician who has been a Teachta Dála (TD) f...







![{\displaystyle r{\frac {(N+1)K}{(N-K+1)(N-K+2)}}[1-{\frac {r}{N-K+1}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e440acb363f2b562dbb11e50df1f9a41a68fd9)






























![{\displaystyle E[Y]=E[X]+r={\frac {r(N+1)}{M+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05ecb17d532fb5fae1a0035199a0f7d9bd302d6d)
