![]() ОњОеОБ ОбОЋОњОћ ОъОдОЎОњ ОЌОюОДОЋ ОЕОю ОЏОю ОъОЋОдОе ОЉОЎОЎОдОЋОе ОћОЏОЋОюОю ОЕОю ОЏОю ОћОъОЋОдОеОЎОЮ
ОњОеОБ ОбОЋОњОћ ОъОдОЎОњ ОЌОюОДОЋ ОЕОю ОЏОю ОъОЋОдОе ОЉОЎОЎОдОЋОе ОћОЏОЋОюОю ОЕОю ОЏОю ОћОъОЋОдОеОЎОЮ
ОњОеОБ ОбОЋОњОћ (ОћОъОЋОЏОе ОњОЮ ОЏОфОеОЕОЎОЮ ОбОЋОњОћ, ОЊОЎОљОњОеОъОф ОбОЋОњОћ ОљОЋ ОЊОЎОљОњОеОъОф ОцОљОЎ) ОћОЋОљ ОфОеОЕОЎОЮ ОАОўОўОЎОАОўОЎ ОЉОбОю ОдОЋОеОћ ОъОбОњОюОЎОф, ОЕОъОЌОЋОюОД ОюОњОќОеОЋОф ("ОцОеОЋОАОЋОф ОбОЋОњОћ") ОљОЕОе ОъОфОљОеОЋОф ОЌОюОЋОДОћ ОЏОъОЋОфОЎОф ОЎОЌОАОЎОф. ОњОЋОЊОю ОЏОю Оњо┤ОќОеОћ ОъОЎОЎОдОњ ОљОф ОњОЋОЊОю ОћОЌОюОД ОћОЎОЌОАОЎ ОЕОћОЎОљ ОъОЎОЎОдОњОф. ОћОфОеОЕОЎОЮ ОъОљОцОЕОе ОћОЕОЋОЋОљОф ОћОЎОЌОА ОЉОЎОЪ ОћОњОќОеОЋОф ОЋОЉОЎОЪ ОЏОю ОњОќОеОћ ОюОбОЋОњОћ ОЏОЋОюОћ.
ОљОЋОеОџ ОћОДОЕОф ОЕОю ОЏОю ОцОеОЋОАОћ, ОЋОЏОфОЋОдОљОћ ОъОЏОџ ОњОЮ ОћОќОЋОЋОЎОф ОћОъОеОЏОќОЎОф ОЕОюОћ ОЋОЕОўОЌОћ, ОцОеОЋОцОЋОеОдОЎОЋОаОюОЎОЎОЮ ОюОъОАОцОе ОљОЋ ОюОЌОюОДОЎОЋОф ОЕОљОЋОфОЮ ОћОЮ ОъОЎОЎОдОњОЎОЮ. ОћОбОЋОњОћ ОъОЋОдОњОф ОЉОдОЋОеОф ОъОбОњОю, ОћОъОћОЋОЋОћ ОЉОъОюОЋОљОЋ ОљОф ОъОљОф ОћОљОЌОЋОќОЎОЮ (ОћОЕОюОЮ), ОЋОъОЌОЋОюОД ОюОњОќОеОЋОф ОЏОъОАОцОе ОћОДОўОњОЋОеОЎОЋОф. ОЕОўОЌ ОЏОю ОњОќОеОћ ОћОЋОљ ОЕОЏОЎОЌОЋОфОћ ОћОЎОЌОАОЎОф ОъОЏОюОю ОћОаОфОЋОаОЎОЮ. ОћОЕОЎОъОЋОЕ ОЉОфОеОЕОЎОъОЎ ОбОЋОњОћ ОаОцОЋОЦ, ОЏОЕОеОЋОдОЎОЮ ОюОћОЕОЋОЋОф ОљОф ОћОЕОюОЮ ОюОЌОюОДОЎОЋ ОЋОљОф ОЌОюОДОЎОЋ ОљОюОЋ ОюОљОюОЋ.
ОАОЋОњ ОќОћ ОЕОю ОћОњОеОБ ОъОфОљОЎОЮ ОъОљОЋОЊ ОюОћОдОњОф ОфОеОЋОъОфОЋ ОЕОю ОЏОю ОЌОюОД ОюОъОЏОюОЋОю ОЕОю ОЏОю ОћОЌОюОДОЎОЮ. ОњОеОБ ОбОЋОњОћ ОаОЎОфОЪ ОюОЕОЎОъОЋОЕ ОеОД ОЉОъОДОеОћ ОЕОъОАОцОе ОћОцОюОЌОЎОЮ ОъОЋОбОў ОЎОЌОАОЎОф (ОбОЊ 5). ОЕОЎОъОЋОЕ ОЉОъОАОцОе ОеОЉ ОЕОю ОћОцОюОЌОЎОЮ ОъОЋОеОЎОЊ ОъОћОЎОбОЎОюОЋОф ОЕОю ОћОњОеОБ ОЏОЎ ОћОЋОљ ОъОДОЕОћ ОбОю ОћОЕОЋОЋОљОф ОћОцОюОЌОЎОЮ, ОЋОћОћОЉОЊОюОЎОЮ ОЉОЎОаОЎОћОЮ ОћОЋОцОЏОЎОЮ ОюОюОљ ОъОЕОъОбОЋОфОЎОЎОЮ.
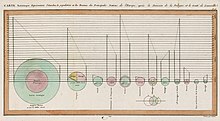 ОфОеОЕОЎОЮ ОћОбОЋОњОћ ОЕОЕОЎОеОўОў ОцОюОЎОЎОцОе ОЉ-1801
ОфОеОЕОЎОЮ ОћОбОЋОњОћ ОЕОЕОЎОеОўОў ОцОюОЎОЎОцОе ОЉ-1801 ОфОеОЕОЎОЮ ОбОЋОњОћ ОЕОю ОЋОЎОюОЎОљОЮ ОцОюОЎОЎОцОе 1801
ОфОеОЕОЎОЮ ОбОЋОњОћ ОЕОю ОЋОЎОюОЎОљОЮ ОцОюОЎОЎОцОе 1801
ОћОЎОАОўОЋОеОЎОћ
ОћОЕОЎОъОЋОЕ ОћОДОЊОЋОЮ ОЉОЎОЋОфОе ОЉОфОеОЕОЎОъОЎ ОбОЋОњОћ ОъОЎОЋОЌОА ОюОЋОЋОЎОюОЎОљОЮ ОцОюОЎОЎОцОе ОЉОАОцОеОЋ ОћОАОўОўОЎОАОўОЎ "Statistical Breviary" ОъОЕОаОф 1801. ОЉОАОцОеОЋ ОћОЋОљ ОћОдОЎОњ ОЕОаОЎ ОфОеОЕОЎОъОЎ ОбОЋОњОћ ОЕОЋОаОЎОЮ. ОцОюОЎОЎОцОе ОћОдОЎОњ ОЕОеОўОЋОў ОЕОћОЏОЎОю ОАОЊОеОћ ОЕОю ОфОеОЕОЎОъОЎ ОбОЋОњОћ. ОљОЌОЊ ОъОљОЋОфОЮ ОфОеОЕОЎОъОЎОЮ ОъОфОљОе ОљОф ОћОЎОЌОАОЎОЮ ОЕОю ОћОљОЎОъОцОеОЎОћ ОћОўОЋОеОДОЎОф ОЕОћОЎОЎОфОћ ОъОъОЋОДОъОф ОЉОљОАОЎОћ, ОЉОљОЎОеОЋОцОћ ОЋОЉОљОцОеОЎОДОћ ОюОцОаОЎ ОЕОаОф 1789.
ОћОЕОЎОъОЋОЕ ОЉОњОеОцОЎОЮ ОъОбОњОюОЎОЎОЮ ОюОљ ОћОЎОЋ ОЉОЕОЎОъОЋОЕ ОаОеОЌОЉ ОЉОфОЌОЎОюОћ. ОћОъОћОаОЊОА ОћОдОеОцОфОЎ Charles Joseph Minard ОћОЎОћ ОљОЌОЊ ОћОеОљОЕОЋОаОЎОЮ ОЕОћОЕОфОъОЕОЋ ОЉОфОеОЕОЎОъОЎ ОбОЋОњОћ ОЉОъОцОЋОф. ОЉОъОцОћ ОЕОюОЋ ОъОЕОаОф 1858, ОћОЋОљ ОћОЕОфОъОЕ ОЉОфОеОЕОЎОЮ ОбОЋОњОћ ОЏОЊОЎ ОюОЎОЎОдОњ ОљОф ОЏОъОЋОЎОЋОф ОћОЉОДОе ОЕОаОЕОюОЌОЋ ОъОЏОю ОеОЌОЉОЎ ОдОеОцОф ОюОдОеОЎОЏОћ ОЉОцОеОЎОќ. Minard ОћОљОъОЎОЪ ОЏОЎ ОюОфОеОЕОЎОъОЎ ОбОЋОњОћ ОаОЊОеОЕ ОъОъОЊ ОЕОюОЎОЕОЎ ОюОдОЋОеОџ ОћОдОњОф ОъОЎОЊОб ОаОЋОАОБ.
ОЎОЕ ОЕОъОЎОЎОЌОАОЎОЮ ОљОф ОћОЕОЎОъОЋОЕ ОћОеОљОЕОЋОаОЎ ОЉОфОеОЕОЎОъОЎ ОбОЋОњОћ ОюОцОюОЋОеОаОА ОаОЎОЎОўОЎОаОњОЎОЎОю, ОюОъОеОЋОф ОЕОЉОцОЋОбОю ОћОЎОљ ОцОЕОЋОў ОћОцОЏОћ ОљОф ОћОЕОЎОъОЋОЕ ОЉОфОеОЕОЎОъОЎ ОбОЋОњОћ ОюОцОЋОцОЋОюОеОЎ.
ОЕОЎОъОЋОЕ, ОЎОбОЎОюОЋОф ОЋОфОцОЎОАОћ ОЌОќОЋОфОЎОф
ОљОЌОЊ ОћОЌОАОеОЋОаОЋОф ОЕОю ОфОеОЕОЎОъОЎ ОбОЋОњОћ ОћОЋОљ ОЕОћОЮ ОъОфОљОЎОъОЎОЮ ОюОћОдОњОф ОъОАОцОе ОбОеОЏОЎОЮ ОЉОЋОЊОЊОЎОЮ. ОЏОљОЕОе ОЏОъОЋОф ОћОбОеОЏОЎОЮ ОњОЊОЋОюОћ, ОаОЊОеОЕОф ОћОцОеОЊОф ОћОДОЎОЊОЋОЊ ОћОЌОќОЋОфОЎ ("ОцОеОЋОАОЋОф") ОъОћОаОфОЋОаОЎОЮ ОЕОћОЮ ОъОЎОЎОдОњОЎОЮ (ОЉОЊОеОџ ОЏОюОю ОЉОљОЌОЋОќОЎОЮ) ОЉОљОъОдОбОЋОф ОЕОЎОъОЋОЕ ОЉОдОЉОбОЎОЮ ОЕОЋОаОЎОЮ, ОЉОъОеОДОъОЎОЮ ОъОЋОЊОњОЕОЎОЮ ОљОЋ ОЉОЌОдОЎОЮ ОЏОЊОЎ ОюОћОДОю ОбОю ОћОЉОаОф ОћОфОеОЕОЎОЮ. ОЉОаОЋОАОБ, ОфОеОЕОЎОъОЎ ОбОЋОњОћ ОфОЋОцОАОЎОЮ ОъОДОЋОЮ ОеОЉ ОЎОЋОфОе ОбОю ОћОЊОБ ОъОљОЕОе ОфОеОЕОЎОъОЎ ОћОбОъОЋОЊОЋОф. ОАОўОўОЎОАОўОЎОДОљОЎОЮ ОЉОЊОеОџ ОЏОюОю ОъОбОЊОЎОцОЎОЮ ОюОћОЎОъОаОб ОъОюОћОЕОфОъОЕ ОЉОфОеОЕОЎОЮ ОбОЋОњОћ ОЏОЕОЎОўОћ ОюОћОдОњОф ОъОЎОЊОб, ОЋОюОЏОЪ ОћОЮ ОъОЋОцОЎОбОЎОЮ ОЉОАОцОеОЋОф ОћОъОДОдОЋОбОЎОф ОеОД ОюОбОЎОфОЎОЮ ОеОЌОЋОДОЋОф. ОЏОЕОъОЉОДОЕОЎОЮ ОюОћОЉОюОЎОў ОаОфОЋОаОЎОЮ ОъОАОЋОЎОъОЎОЮ, ОъОЋОцОеОЊОЋОф ОћОцОеОЋОАОЋОф ОћОъОЎОЎОдОњОЋОф ОљОЋОфОЮ ОаОфОЋОаОЎОЮ ОъОЕОљОе ОћОЊОЎОљОњОеОъОћ ОЋОъОЋОдОњОЋОф ОЉОъОеОЌОД ОъОћ ОъОъОаОћ.
 ОЉОфОеОЕОЎОЮ ОћОЉОљ ОъОЋОдОњОЎОЮ ОЕОюОЋОЕОћ ОфОеОЕОЎОъОЎ ОбОЋОњОћ, ОЋОъОфОЌОф ОюОЏОЋОю ОљОЌОЊ ОъОфОеОЕОЎОъОЎ ОћОбОЋОњОћ ОъОЋОдОњОЎОЮ ОљОЋОфОЮ ОћОаОфОЋОаОЎОЮ ОЉОњОеОБ ОбОъОЋОЊОЋОф. ОЉОфОеОЕОЎОЮ ОќОћ ОДОю ОюОеОљОЋОф ОЏОЎОдОЊ ОфОеОЕОЎОъОЎ ОбОъОЋОЊОЋОф ОцОЕОЋОўОЎОЮ ОЎОЋОфОе ОюОцОбОаОЋОЌ ОъОљОЕОе ОфОеОЕОЎОъОЎ ОбОЋОњОћ.
ОЉОфОеОЕОЎОЮ ОћОЉОљ ОъОЋОдОњОЎОЮ ОЕОюОЋОЕОћ ОфОеОЕОЎОъОЎ ОбОЋОњОћ, ОЋОъОфОЌОф ОюОЏОЋОю ОљОЌОЊ ОъОфОеОЕОЎОъОЎ ОћОбОЋОњОћ ОъОЋОдОњОЎОЮ ОљОЋОфОЮ ОћОаОфОЋОаОЎОЮ ОЉОњОеОБ ОбОъОЋОЊОЋОф. ОЉОфОеОЕОЎОЮ ОќОћ ОДОю ОюОеОљОЋОф ОЏОЎОдОЊ ОфОеОЕОЎОъОЎ ОбОъОЋОЊОЋОф ОцОЕОЋОўОЎОЮ ОЎОЋОфОе ОюОцОбОаОЋОЌ ОъОљОЕОе ОфОеОЕОЎОъОЎ ОбОЋОњОћ.
ОљОЌОф ОћОАОЎОЉОЋОф ОюОЏОџ ОЕОфОеОЕОЎОъОЎ ОбОЋОњОћ ОљОЎОаОЮ ОќОЋОЏОЎОЮ ОюОцОЋОцОЋОюОеОЎОЋОф ОЉОДОћОЎОюОф ОћОАОўОўОЎОАОўОЎОДОљОЎОЮ, ОћОЎОљ ОЕОюОћОбОеОЏОфОЮ ОДОЕОћ ОЎОЋОфОе ОюОћОбОеОЎОџ ОЋОЎОќОЋОљОюОЎОф ОћОЉОЊОюОЎОЮ ОЉОЕОўОЌ ОъОљОЕОе ОћОЉОЊОюОЎОЮ ОЉОњОЋОЉОћ (ОЏОъОЋ ОЉОњОеОБ ОбОъОЋОЊОЋОф). ОЎОфОе ОбОю ОЏОЪ, ОЉОъОЌОДОе ОЕОЉОЋОдОб ОЉОъОбОЉОЊОЋОф ОЕОю AT & T Bell, ОћОЋОЏОЌ ОЏОЎ ОћОЕОЋОЋОљОћ ОћОаОбОЕОЎОф ОбОю ОЎОЊОЎ ОќОЋОЋОЎОф, ОъОЊОЋОЎОДОф ОцОЌОЋОф ОъОћОЕОЋОЋОљОћ ОюОцОЎ ОљОЋОеОџ.
ОЌОЕОЋОЉ ОюОћОЊОњОЎОЕ, ОЏОЎ ОЏОљОЕОе ОћОъОўОеОћ ОћОЎОљ ОюОћОЕОЋОЋОф ОДОўОњОЋОеОЎОћ ОъОАОЋОЎОъОф (ОцОеОЋОАОф ОћОбОЋОњОћ) ОЉОЎОЌОА ОюОЏОюОю ОћОЕОюОЮ (ОЏОю ОћОбОЋОњОћ) ОЋОДОЎОЎОъОЎОЮ ОъОАОцОе ОбОеОЏОЎОЮ (ОцОеОЋОАОЋОф) ОЉОЋОЊОЊОЎОЮ, ОЎОЏОЋОю ОфОеОЕОЎОЮ ОбОЋОњОћ ОЎОЏОЋОю ОюОћОЎОЋОф ОюОбОЎОфОЎОЮ ОДОеОЋОЉОЋОф ОЎОбОЎОю ОЎОЋОфОе ОъОњОеОБ ОбОъОЋОЊОЋОф. ОЊОЎОљОњОеОъОф ОбОЋОњОћ ОЕОЎОъОЋОЕОЎОф ОюОфОЎОљОЋОе ОъОЕОфОаОћ ОъОАОЋОюОЮ ОъОЊОЎОЊОћ ОЕОъОЎ.
ОЎОдОЎОеОф ОфОеОЕОЎОъОЎ ОбОЋОњОћ
-
ОЊОЎОљОњОеОъОф ОбОЋОњОћ ОцОЕОЋОўОћ: ОцОЎОюОЋОЌ ОљОЋОЏОюОЋОАОЎОЎОф ОЉОбОюОЎ ОўОюОцОЋОЪ ОћОљОаОЊОеОЋОљОЎОЊ ОюОцОЎ ОЊОњОъОЎ ОћОўОюОцОЋОЪ, ОаОЏОЋОЪ ОюОЕОаОф 2010. ОЎОеОЋОД ОќОЎОф РђЊ ОљОЌОЋОќОЎ ОЉОбОюОЎ ОЊОњОЮ 2.1, ОАОњОЋОю РђЊ ОљОЌОЋОќОЎ ОЉОбОюОЎ ОЊОњОЮ 2.2, ОфОЏОюОф РђЊ ОљОЌОЋОќОЎ ОЉОбОюОЎ ОЊОњОЮ 1.5 ОЋОЌОЋОЮ ОљОЊОъОЊОЮ РђЊ ОљОЌОЋОќОЎ ОЉОбОюОЎ ОЊОњОЮ 1.6.
-
ОфОеОЕОЎОЮ ОбОЋОњОћ ОЉОфОЋОџ ОфОеОЕОЎОЮ ОбОЋОњОћ РђЊ ОЊОеОџ ОаОЋОЌОћ ОюОћОЕОЋОЋОф ОЕОаОЎ ОфОеОЕОЎОъОЎ ОбОЋОњОћ ОЊОЋОъОЎОЮ, ОљОџ ОюОљ ОќОћОЎОЮ.
-
ОЊОЎОљОњОеОъОф ОбОЋОњОћ ОЉОЕОЎОюОЋОЉ ОдОЎОюОЋОъОЎ ОћОъОЌОЕОћ, ОћОъОЕОЋОЋОћ ОљОф ОЏОъОЋОф ОћОДОеОДОб ОЉОЉОюОњОЎОћ, ОЕОћОЋОДОдОфОћ ОюОЌОДОюОљОЋОф, ОюОЎОбОЊ, ОюОЉОаОЎОЎОћ ОЋОюОЊОЉОеОЎОЮ ОљОЌОеОЎОЮ.
-
ОЊОЎОљОњОеОъОф ОбОЋОњОћ, ОЕОљОЌОЊ ОъОцОюОЌОЎОћ ОъОцОЋОюОЌ ОњОЮ ОћОЋОљ, ОЉОдОЊ, ОЏОЊОЎОљОњОеОъОф ОбОЋОњОћ
-
ОЊОЎОљОњОеОъОф ОбОЋОњОћ ОфОюОф ОъОъОЊОЎОф ОбОЮ ОцОюОЌОЎОЮ ОъОЋОеОЌОДОЎОЮ ОЋОъОЉОў ОъОћОдОЊ: ОфОцОЋОдОћ ОЎОЌОАОЎОф ОЕОю ОЊОцОЊОцОаОЎ ОљОЎОаОўОеОаОў ОЉОљОЎОеОЋОцОћ, ОЉОЕОаОф 2011.
-
ОДОЎОЕОЋОеОЎОЮ ОЌОЎОдОЋОаОЎОЎОЮ