גרף מקרי
| ||||||||||||
Read other articles:

Rumah Sakit Umum Pusat Dr. SardjitoKementerian Kesehatan Republik IndonesiaGeografiLokasiJl. Kesehatan No. 1, Sekip Sinduadi, Sleman, Daerah Istimewa Yogyakarta, IndonesiaKoordinat7°46′5″S 110°22′22″E / 7.76806°S 110.37278°E / -7.76806; 110.37278Koordinat: 7°46′5″S 110°22′22″E / 7.76806°S 110.37278°E / -7.76806; 110.37278OrganisasiAsuransi kesehatanBPJS KesehatanPendanaanRumah sakit publikJenisRumah sakit umumAfiliasi den...

Chinese insurance company This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Ping An Insurance – news · newspapers · books · scholar · JSTOR (March 2022) (Learn how and when to remove this template messag...

Peter GoldreichPeter Goldreich pada 1980Lahir14 Juli 1939 (umur 84)Tempat tinggalPasadenaAlmamaterUniversitas CornellDikenal atasEfek Goldreich-KylafisPenghargaanMedali Chapman Royal Astronomical Society (1985)[1] Penghargaan Brouwer (1986) Medali Emas Royal Astronomical Society (1993)[2][3] Medali Sains Nasional (1995) Penghargaan Shaw (2007)Karier ilmiahBidangAstronomi dan AstrofisikaInstitusiCaltechInstitut Studi LanjutanPembimbing doktoralThomas GoldMahasiswa...

Pembagian administratif Israel tingkat pertama Pembagian administratif Israel tingkat pertama terdiri atas 6 distrik (מָחוֹז, mahoz). Tingkat kedua adalah 15 subdistrik (נָפָה, nafa). Tingkat ketiga terdiri atas 76 arimci, 265 moatzot mekomiot, dan 53 moatzot azoriot. lbsPembagian administratif AsiaNegaraberdaulat Afganistan Arab Saudi Armenia1 Azerbaijan1 Bahrain Bangladesh Bhutan Brunei Filipina Georgia1 India Indonesia Irak Iran Israel Jepang Kamboja Kazakhstan3 Kirgizstan Korea...

Шалфей обыкновенный Научная классификация Домен:ЭукариотыЦарство:РастенияКлада:Цветковые растенияКлада:ЭвдикотыКлада:СуперастеридыКлада:АстеридыКлада:ЛамиидыПорядок:ЯсноткоцветныеСемейство:ЯснотковыеРод:ШалфейВид:Шалфей обыкновенный Международное научное наз...

Japanese animator and manga artist (born 1941) The native form of this personal name is Miyazaki Hayao. This article uses Western name order when mentioning individuals. Hayao Miyazaki宮崎 駿Miyazaki in 2012Born (1941-01-05) January 5, 1941 (age 83)Tokyo City, Tokyo Prefecture, Empire of JapanOther namesAkitsu Saburō (秋津 三朗)Teruki Tsutomu (照樹 務)Alma materGakushuin UniversityOccupationsAnimatorfilmmakerscreenwriterauthormanga artistYears active1963–p...

1966 song written by Chip Taylor Any Way That You Want MeWest German picture sleeveSingle by the TroggsB-side66-5-4-3-2-1Released9 December 1966 (1966-12-09)[1]Genre Baroque pop pop rock Length2:57LabelPage OneSongwriter(s)Chip TaylorProducer(s)Larry PageThe Troggs singles chronology I Can't Control Myself (1966) Any Way That You Want Me (1966) Give It to Me (1967) Any Way That You Want Me is a song written by Chip Taylor that was first released in September 1966 by Tin...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (يونيو 2023) يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة ...

Macedonian footballer (born 1985) Muharem Bajrami Personal informationDate of birth (1985-11-29) 29 November 1985 (age 38)Place of birth Skopje, SFR YugoslaviaHeight 1.85 m (6 ft 1 in)Position(s) MidfielderSenior career*Years Team Apps (Gls)2004–2005 Sloga Jugomagnat 2005–2006 Vëllazërimi 25 (15)2006–2007 FBK Kaunas 5 (0)2008 Šilutė 17 (4)2009–2012 Renova 95 (22)2013 Gomel 1 (0)2013 Shkëndija 10 (1)2014–2020 Shkupi 145 (16)International career2002 Macedonia ...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Mechanical component for transmitting torque and rotation This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Drive shaft – news · newspapers · books · scholar · JSTOR (June 2010) (Learn how and when to remove this message) Drive shaft with universal joints at each end and a spline in the centre 3D animation of ...

Danish Church in Southern SchleswigDansk Kirke i SydslesvigChurch of the Holy Spirit (Danish: Helligåndskirken) in FlensburgAbbreviationDKSClassificationProtestantOrientationLutheranRegionSouthern SchleswigLanguageDanishHeadquartersFlensburgBranched fromChurch of DenmarkCongregationsc. 30Membersc. 6,000Official websitewww.dks-folkekirken.dk The Danish Church in Southern Schleswig (Danish: Dansk Kirke i Sydslesvig) is an evangelical Lutheran church in Southern Schleswig in Northern Germany. T...

Beer of New Zealand Epic pale ale Beer is the most popular alcoholic drink in New Zealand, accounting for 63% of available alcohol for sale.[1] At around 64.7 litres per person per annum, New Zealand is ranked 27th in global beer consumption per capita. The vast majority of beer produced in New Zealand is a type of lager, either pale or amber in colour, and typically 4–5% alcohol by volume.[2] Although the two largest breweries in New Zealand, Lion Nathan and DB Breweries, c...

This article discusses banking in Cuba and gives an overview of the recent past. For details on the Cuban economy in general, see economy of Cuba. History Following the Cuban Revolution of the 1950s, the Cuban banking sector came under the control of the new regime. The new authorities famously appointed Che Guevara as President of the National Bank of Cuba (Spanish: Banco Nacional de Cuba) in 1959. Guevara often retold the apocryphal story of how he gained the job at the bank; Fidel Castro h...
Эта статья содержит информацию о запланированном или ожидаемом телесериале. Содержание может меняться коренным образом по мере приближения даты выхода сериала и появления новой информации. Об одноимённой сюжетной линии в комиксах см. Daredevil: Born Again. У этого термина �...

Jorge Gotor Blas Jorge Gotor Presentation Atlético Baleares, 2012Informasi pribadiNama lengkap Jorge Gotor BlasTanggal lahir 14 April 1987 (umur 37)Tempat lahir Zaragoza, SpanyolTinggi 187 m (613 ft 6 in)Posisi bermain BekInformasi klubKlub saat ini Mitra KukarKarier junior Santo Domingo UD AmistadKarier senior*Tahun Tim Tampil (Gol)2005-2008 Real Zaragoza B 2008-2009 RCD Espanyol B 32 (3)2009-2011 Real Murcia 47 (6)2012 Getafe B 32 (3)2012 Atlético Baleares 8 (3)2013 C...

Former women's basketball team San Antonio StarsConferenceWesternLeaguesWNBAFounded1997HistoryUtah Starzz(1997–2002)San Antonio Silver Stars(2003–2013)San Antonio Stars(2014–2017)Las Vegas Aces(2018–present)ArenaAT&T CenterLocationSan Antonio, TexasTeam colorsSilver, black[1][2] OwnershipSpurs Sports & EntertainmentChampionships0Conference titles1 (2008)Retired numbers1 (25) Home Away The San Antonio Stars were a professional basketball team based i...

В Википедии есть статьи о других людях с фамилией Франсуа. Жак Франсуафр. Jacques François Имя при рождении Henri Jacques Daniel Paul François Дата рождения 16 мая 1920(1920-05-16) Место рождения Париж, Франция Дата смерти 25 ноября 2003(2003-11-25) (83 года) Место смерти Париж, Франция Гражданство &#...

Angoulême Façade du bâtiment voyageurs en 2018 avec l’obélisque sur la droite. Localisation Pays France Commune Angoulême Quartier L'Houmeau Adresse 4, place de la Gare16022 Angoulême Cedex Coordonnées géographiques 45° 39′ 13″ nord, 0° 09′ 52″ est Gestion et exploitation Propriétaire SNCF Exploitant SNCF Code UIC 87583005 Site Internet La gare d'Angoulême, sur le site officiel de SNCF Gares & Connexions Services TGV inOui et OuigoTER N...
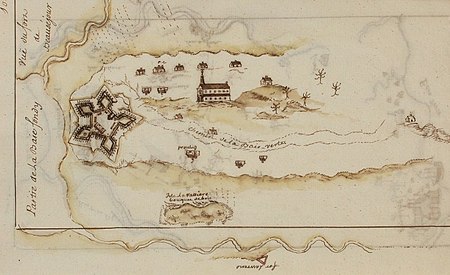
Fort in Aulac, New Brunswick, Canada Fort BeauséjourAulac, New Brunswick Fort Beauséjour and Cathedral (c. 1755)Coordinates45°51′53″N 64°17′29″W / 45.86472°N 64.29139°W / 45.86472; -64.29139TypeFortressSite informationControlled byFrance (1751–1755), United Kingdom (1755–1835), Parks Canada (1926–present) National Historic Site of CanadaOfficial nameFort Beauséjour – Fort Cumberland National Historic Site of CanadaDesignated1920 Site history...






















