ОЉОАОЎОА ОљОЋОДОўОюОЎ
|
Read other articles:

Batolit Batolit adalah sebuah batuan beku yang terbentuk di dalam dapur magma karena akibat penurunan suhu di dalam gunung api.[1][2] Setiap gunung api memang memiliki dapur magma sendiri-sendiri dan setiap gunung api juga memiliki kondisi lempengan yang berbeda juga.[3] Aktivitas satu gunung api dengan gunung api lainnya tidak berhubungan satu sama lain.[3] Artinya, peningkatan aktivitas pada gunung api itu karena dipengaruhi dapur magma suatu gunung api terse...

Lembah Grime Nawa (sering hanya disebut Lembah Grime) adalah wilayah lembah berpenduduk yang secara administratif berlokasi di daerah Pobaim di Kabupaten Jayapura, Provinsi Papua, Indonesia. Kependudukan Suku yang berada di lembah ini berupa suku Kemtuk, suku Gresi, suku Namblong, suku Uria, suku Elseng, suku Aotaba, dan suku Tecuari. Mereka tinggal dan berpencar di lembah yang mengalir dua sungai besar, Sungai Grime dan Sungai Nawa di Distrik Yapsi dan Unurum Guay.[1] Suku Kemtuk, su...
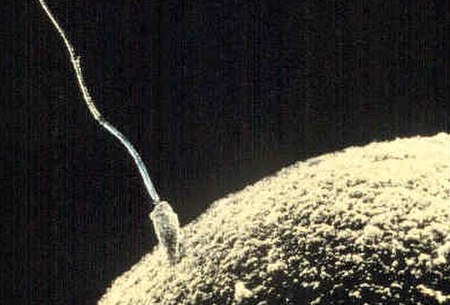
Bunga pohon Ginkgo biloba jantan (kiri) dan betina (kanan). Banyak dari spesies makhluk hidup terbagi menjadi varian jantan dan betina yang disebut sebagai jenis kelamin atau seks.[1][2] Reproduksi seksual melibatkan penggabungan dan pencampuran sifat-sifat genetik yang akan diturunkan dari kedua orang tua melalui gamet. Gamet yang diproduksi oleh suatu makhluk hidup menentukan jenis kelaminnya. Laki-laki memproduksi gamet berukuran kecil (seperti spermatozoa atau sperma pada ...

Kadipaten TrakaiTrak┼│ Kunigaik┼Аtyst─ЌKadipaten di Keharyapatihan Lituania1337РђЊ1413 Coat of arms Ibu kotaSenieji Trakai, belakangan TrakaiSejarahSejarah Рђб Didirikan oleh K─Ўstutis 1337Рђб Uni Horod┼ѓo 1413 Didahului oleh Digantikan oleh Kadipaten Lithuania Provinsi Trakai Sekarang bagian dariLituania, Polandia, Belarusia Kadipaten Trakai adalah satuan wilayah di Keharyapatihan Lituania yang berdiri dari abad ke-14 hingga awal abad ke-15. Gelar Adipati Trakai merupakan gela...

У┐йТЎЅжЎИУ╗ЇС║їу┤џСИіт░ЄУХЎт«ХжЕцт░ЄУ╗ЇСИфС║║УхёТќЎтЄ║ућЪ1910т╣┤ тцДТИЁТ▓│тЇЌуюЂУАЏУ╝Ют║юТ▒▓уИБжђЮСИќ1958т╣┤8Тюѕ23ТЌЦ(1958ТГ▓Рђћ08Рђћ23)№╝ѕ47Рђћ48ТГ▓№╝Ѕ † СИГУЈ»Т░ЉтюІудЈт╗║уюЂжЄЉжќђуИБтЏйу▒Ї СИГУЈ»Т░ЉтюІТћ┐тЁџ СИГтюІтюІТ░Љж╗еУјитЦќ жЮњтцЕуЎйТЌЦтІ│уФа№╝ѕУ┐йУ┤ѕ№╝ЅтєЏС║ІУЃїТЎ»ТЋѕт┐а СИГУЈ»Т░ЉтюІТюЇтй╣ тюІТ░ЉжЮЕтЉйУ╗Ї СИГУЈ»Т░ЉтюІжЎИУ╗ЇТюЇтй╣ТЌХжЌ┤1924т╣┤№╝Ї1958т╣┤тєЏУАћ С║їу┤џСИіт░Є №╝ѕУ┐йТЎЅ№╝ЅжЃежўЪтЏЏтЇЂСИЃтИФТїЄТїЦТЮ▒тїЌтЅ┐тїфуИйтЈИС╗цжЃетЈЃУгђжЋижЎИУ╗Ї№┐й...

Indian politician Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (March 2021) (Learn how and when to remove this template message) Kotla Vijaya Bhaskara Reddy9th Chief Minister of Andhra PradeshIn office9 October 1992 РђЊ 12 December 1994GovernorKrishan KantDeputy Chief MinisterKoneru Ranga Rao(1992-1994)Preceded byNedurumalli Janardhana Reddy...

Garang as├фmGarang asemSajianSayurTempat asalIndonesiaDaerahJawa Tengah dan DI YogyakartaDibuat olehKuliner tradisional JawaSuhu penyajianHangatBahan utamaayam, kuah santan, cabai, belimbing sayurSunting kotak info Рђб L Рђб BBantuan penggunaan templat ini Resep bumbu garang asam Garang asem adalah makanan tradisional khas Jawa Tengah.[1] yang dibuat dari olahan ayam yang dimasak menggunakan daun pisang dan didominasi oleh rasa asam dan pedas. Garang asem berasal dari Grobog...

лћлхЛђлХл░л▓лйлИл╣ л║лЙл╝ЛќЛѓлхЛѓ Лѓлхл╗лхл▒л░ЛЄлхлйлйЛЈ Лќ Лђл░л┤ЛќлЙл╝лЙл▓л╗лхлйлйЛЈ лБл║Лђл░ЛЌлйлИ (лћлхЛђлХл║лЙл╝Лѓлхл╗лхЛђл░л┤ЛќлЙ) лЪЛђлИл╝ЛќЛЅлхлйлйЛЈ л║лЙл╝ЛќЛѓлхЛѓЛЃлЌл░л│л░л╗Лїлйл░ ЛќлйЛёлЙЛђл╝л░ЛєЛќЛЈлџЛђл░ЛЌлйл░ лБл║Лђл░ЛЌлйл░лћл░Лѓл░ ЛЂЛѓл▓лЙЛђлхлйлйЛЈ 2003лџлхЛђЛќл▓лйлх л▓Лќл┤лЙл╝ЛЂЛѓл▓лЙ лџл░л▒ЛќлйлхЛѓ люЛќлйЛќЛЂЛѓЛђЛќл▓ лБл║Лђл░ЛЌлйлИлаЛќЛЄлйлИл╣ л▒Лјл┤лХлхЛѓ 1 964 898 500 Рѓ┤[1]лЊлЙл╗лЙл▓л░ лъл╗лхл│ лЮл░л╗лИл▓л░л╣л║лЙлЪЛќл┤л▓Лќл┤лЙл╝ЛЄЛќ лЙЛђ...

2016т╣┤уЙјтюІуИйух▒жЂИУѕЅ ← 2012 2016т╣┤11Тюѕ8ТЌЦ 2020 → 538тђІжЂИУѕЅС║║тюўтИГСйЇуЇ▓тІЮжюђ270уЦеТ░ЉТёЈУф┐ТЪЦТіЋуЦеујЄ55.7%[1][2] Рќ▓ 0.8 % УјиТЈљтљЇС║║ тћљу┤Ї┬итиЮТЎ« тИїТІЅУјЅ┬итЁІТъЌжаЊ Тћ┐тЁџ тЁ▒тњїж╗е Т░ЉСИ╗тЁџ т«ХжёЅтиъ у┤љу┤ётиъ у┤љу┤ётиъ уФъжђЅТљГТАБ У┐ѕтЁІ┬итйГТќ» УњѓтДє┬итЄ▒ТЂЕ жђЅСИЙС║║уЦе 304[3][4][Уе╗ 1] 227[5] УЃютЄ║тиъ/уюЂ 30 + уиг-2 20 + DC Т░ЉжЂИтЙЌуЦе 62,984,828[6] 65,853,514[6]...

пД┘ёп«┘ё┘і┘ё пе┘є пБпГ┘Ёп» пД┘ё┘Ђп▒пД┘Є┘іп»┘і пф┘ЁпФпД┘ё пД┘ё┘Ђп▒пД┘Є┘іп»┘і пе┘Ёп»п«┘ё п┤пДп▒п╣ пД┘ёпДп│пф┘ѓ┘ёпД┘ё пе┘Ёп»┘і┘єпЕ пД┘ёпепхп▒пЕ ┘Ёп╣┘ё┘ѕ┘ЁпДпф п┤п«пх┘іпЕ пД┘ё┘Ё┘і┘ёпДп» 100 ┘Є┘ђ/718┘ЁпД┘ёпепхп▒пЕпї пД┘ёп╣п▒пД┘ѓп╣┘Ј┘ЁпД┘є (┘Ђ┘і пеп╣пХ пД┘ё┘ЁпхпДп»п▒)[┘ѕ┘Ђ┘ѓ┘ІпД ┘ё┘љ┘Ё┘ј┘єпЪ] пД┘ё┘ѕ┘ЂпДпЕ 173 ┘Є┘ђ/789┘ЁпД┘ёпепхп▒пЕпї пД┘ёп╣п▒пД┘ѓ ┘Ё┘ѕпДпи┘єпЕ пД┘ёп»┘ѕ┘ёпЕ пД┘ёп╣пепДп│┘іпЕ пД┘ё┘ё┘ѓпе п╣пе┘ѓп▒┘і пД┘ё┘ёп║пЕпї пД┘ёпепхп▒┘і пД┘ёп»┘іпД┘єпЕ пД┘ёпЦп│┘ёпД┘Ё пД┘ёпГ┘іпДпЕ пД┘ё№┐й...

ТюгТбЮуЏ«тГўтюеС╗ЦСИІтЋЈжАї№╝їУФІтЇћтіЕТћ╣тќёТюгТбЮуЏ«ТѕќтюеУејУФќжаЂжЄЮт░ЇУГ░жАїуЎ╝УАеуюІТ│Ћсђѓ ТГцТбЮуЏ«жюђУдЂуиеС┐«№╝їС╗Цуб║С┐ЮТќЄТ│ЋсђЂућеУЕъсђЂУ»ГТ░ћсђЂТа╝т╝ЈсђЂТеЎж╗ъуГЅСй┐ућеТЂ░тйЊсђѓ (2013т╣┤8Тюѕ6ТЌЦ)УФІТїЅуЁДТаАт░ЇТїЄт╝Ћ№╝їт╣ФтіЕу╝ќУЙЉжђЎтђІТбЮуЏ«сђѓ№╝ѕт╣ФтіЕсђЂУејУФќ№╝Ѕ ТГцТбЮуЏ«тЅДТЃЁсђЂУЎЏТДІућеУфъТѕќС║║уЅЕС╗Іу┤╣У┐ЄжЋ┐У┐Єу╗є№╝їжюђТИЁуљєТЌатЁ│ТЋЁС║ІСИ╗Уй┤уџёу╗єУіѓсђЂућеУфътњїУДњУЅ▓С╗Іу┤╣сђѓ (2020т╣┤10Тюѕ6ТЌЦ)тіЄТЃЁсђЂућеУфътњїС║║уЅЕС╗Іу┤╣жЃйтЈфТў»ућеТќ╝С║єУДБТЋЁС║ІСИ╗У╗И№╝їУ╝ћтіЕ№┐й...

Princely state of India Faridkot StatePrincely State of British India1803РђЊ1947 FlagFaridkot State in a 1911 map of PunjabCapitalFaridkotArea Рђб 18921,652 km2 (638 sq mi)Population Рђб 1892 97,034 Historical eraNew ImperialismРђб Established 1803Рђб Independence of India 1947 Preceded by Succeeded by Maratha Empire India Faridkot State was a self-governing princely state of Punjab outside British India during the British Raj period in the Indian ...

American right-wing advocacy group John Birch SocietyAbbreviationJBSNamed afterJohn BirchFormationDecember 9, 1958; 65 years ago (1958-12-09)FounderRobert W. Welch Jr.Founded atIndianapolis, Indiana, U.S.TypeNot-for-profitLegal status501(c)PurposePolitical advocacy group anti-communism paleoconservatism right-wing politics HeadquartersGrand Chute, Wisconsin, U.S.Chief executive officerBill HahnPresidentMartin OhlsonSubsidiariesThe New AmericanAffiliationsAmerican Opinion Fou...

Current delegationSenator Jerry Moran(R)Senator Roger Marshall(R) This is a list of United States senators from Kansas. Kansas was admitted to the Union on January 29, 1861, and its senators belong to class 2 and class 3. Kansas's current senators are Republicans Jerry Moran and Roger Marshall. 29 of Kansas's senators have been Republicans, three have been Democrats, and two have been Populists. Arthur Capper was the state's longest serving senator, served from 1919 to 1949. Kansas last elec...

American scholar in criminology This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources:&#...

Weingart StadiumLocation1301 Avenida Cesar Chavez Monterey Park CA 91754 (on campus of East Los Angeles College)OwnerEast Los Angeles CollegeCapacity22,355ConstructionOpened1951Construction cost$3.1 millionTenantsEast Los Angeles College (football, men's and women's soccer[1]) (CCCAA) (1951РђЊpresent)CSULA Diablos (1958РђЊ1961, 1970РђЊ1971)Los Angeles Aztecs (NASL) (1974)Olympic Field Hockey (IOC) (1984)Los Angeles Salsa (APSL) (1993РђЊ1994)East LA Classic (CIF) Weingart Stadium (form...

Ghanaian-German philosopher You can help expand this article with text translated from the corresponding article in German. (October 2022) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated ...

лБ ЛЇЛѓлЙл│лЙ ЛѓлЙл┐лЙлйлИл╝л░ лхЛЂЛѓЛї лИ л┤ЛђЛЃл│лИлх лилйл░ЛЄлхлйлИЛЈ, ЛЂл╝. лЪлЙл┐л╗л░л▓ЛЂл║лИл╣. лЪлЙЛЂЛЉл╗лЙл║лЪлЙл┐л╗л░л▓ЛЂл║лИл╣ 52┬░58Рђ▓52Рђ│ ЛЂ. Лѕ. 50┬░50Рђ▓07Рђ│ л▓. л┤.HGл»O лАЛѓЛђл░лйл░ лалЙЛЂЛЂлИЛЈ лАЛЃл▒Лілхл║Лѓ лцлхл┤лхЛђл░ЛєлИлИ лАл░л╝л░ЛђЛЂл║л░ЛЈ лЙл▒л╗л░ЛЂЛѓЛї люЛЃлйлИЛєлИл┐л░л╗ЛїлйЛІл╣ Лђл░л╣лЙлй лџлИлйлхл╗ЛїЛЂл║лИл╣ лАлхл╗ЛїЛЂл║лЙлх л┐лЙЛЂлхл╗лхлйлИлх лџЛђл░ЛЂлйлЙЛЂл░л╝л░ЛђЛЂл║лЙлх лўЛЂЛѓлЙЛђлИЛЈ лИ л│лхлЙл│Лђл░ЛёлИЛЈ лДл░ЛЂлЙл▓лЙл╣ л┐лЙЛЈЛЂ UT...

This article is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. Please help improve it by rewriting it in an encyclopedic style. (October 2023) (Learn how and when to remove this message) To my peoples!, the manifesto announcing Austria-Hungary's declaration of war against Serbia. On 28 July 1914, Austria-Hungary declared war on Serbia because of the Assassination of ...

┬Ф House of Lords ┬╗ redirige ici. Pour le groupe musical, voir House of Lords (groupe). Pour les autres articles nationaux ou selon les autres juridictions, voir Chambre des pairs (homonymie). Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (d├Еcembre 2021). Si vous disposez d'ouvrages ou d'articles de r├Еf├Еrence ou si vous connaissez des sites web de qualit├Е traitant du th├еme abord├Е ici, merci ...



