Constante de Khinchin
|
Read other articles:

Strada statale 637di Frosinone e di GaetaDenominazioni successiveStrada regionale 637 di Frosinone e di Gaeta LocalizzazioneStato Italia Regioni Lazio DatiClassificazioneStrada statale InizioFrosinone FineFondi Lunghezza52,045[1] km Provvedimento di istituzioneD.M. 19/08/1971 - G.U. 262 del 15/10/1971[2] GestoreANAS (1971-2002) Manuale La ex strada statale 637 di Frosinone e di Gaeta (SS 637), ora strada regionale 637 di Frosinone e di Gaeta (SR 637)[3], era ...

The topic of this article may not meet Wikipedia's notability guideline for music. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Endless Love Jeanette song – news · newspapers · books · scholar · J...

Chaand Kaa Tukdaa चाँद का टुकड़ाMovie posterSutradaraSaawan Kumar TakProduserSaawan Kumar TakDitulis olehAnwar Khan (dialogues)SkenarioSachin BhowmickCeritaSaawan Kumar TakPemeranSrideviSalman KhanPenata musikMahesh-Kishor (songs),Usha Khanna (BGM)SinematograferG. Shyam KumarPenyuntingJawahar RazdanPerusahaanproduksiSaawan Kumar ProductionsTanggal rilis 19 Agustus 1994 (1994-08-19) Durasi155 minutesNegaraIndiaBahasaHindiPendapatankotorper. ₹13 crore (setar...

Chinese American man with queue in San Francisco's Chinatown The Pigtail Ordinance was an 1873 law intended to force prisoners in San Francisco, California to have their hair cut within an inch of the scalp. It affected Qing Chinese prisoners in particular, as it meant they would have their queue, a waist-long, braided pigtail, cut off. The proposal passed by a narrow margin through the San Francisco Board of Supervisors in 1873 but was vetoed by the mayor. An identical version of the law was...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Pristina has only 3 active theatres National Theatre of Kosova, ODA Theatre and DODONA Theatre. They give live performances every week. There are 21 well-known Kosovan actors employed. They are located in the heart of Pristina. National Theatre (Teatri Kombetar) is placed in the middle downtown of the city, near the main government building.[1] ODA Theatre (Teatri ODA) is placed in the Youth Centre Building, and Dodona Theatre (Teatri Dodona) is placed in Vellusha district, which is n...

穆罕默德·达乌德汗سردار محمد داود خان 阿富汗共和國第1任總統任期1973年7月17日—1978年4月28日前任穆罕默德·查希爾·沙阿(阿富汗國王)继任穆罕默德·塔拉基(阿富汗民主共和國革命委員會主席團主席) 阿富汗王國首相任期1953年9月7日—1963年3月10日君主穆罕默德·查希爾·沙阿 个人资料出生(1909-07-18)1909年7月18日 阿富汗王國喀布尔逝世1978年4月28日(...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Tito Cicciò Dati biografici Paese Italia Altezza 193 cm Peso 110 kg Rugby a 15 Ruolo Terza linea centro Ritirato 1997 Carriera Attività giovanile 1980-1986 Messina Attività di club[1] 1986-1998 Milan Attività da giocatore internazionale 1992-1993 Italia5 (0) Attività da allenatore 1998-2000 Clan Messina2000-2003 Reggio Emilia2005-2009 Milazzo2010-2014 Italia Under-172014-2021 Italia FemminileAll. 2ª 1. A partire dalla stagione 1995-96 le statistiche di cl...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Parandra puncticeps Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Parandra Spesies: Parandra puncticeps Parandra puncticeps adalah spesies kumbang tanduk panjang yang tergolong famil...
Елабужский государственный музей-заповедник Дата основания 1989 Дата открытия 09:00 — 18:00, пн — выходной Местонахождение Елабуга Адрес Елабуга, улица Гассара, 9 Посетителей в год от 100 тыс. в год Директор Гульзада Ракиповна Руденко Сайт elabuga.com Медиафайлы на Викискладе Объ�...

Национальное аэрокосмическое агентство Азербайджана Штаб-квартира Баку, ул. С. Ахундова, AZ 1115 Локация Азербайджан Тип организации Космическое агентство Руководители Директор: Натиг Джавадов Первый заместитель генерального директора Тофик Сулейманов Основание Осн�...

Дагестанские народы Современное самоназвание МагIарулал, Лезгияр, Дарганти, Лак Численность и ареал Всего: 5 млн Россия около 4 млн Дагестан 3 332 543 Азербайджан 650 000 Турция ≈ 200 000[1] Казахстан 20 000 Туркменистан 20 000 [оценка 2020 года] Описание Язык дагеста�...

Men's 800 metres at the 2013 World ChampionshipsVenueLuzhniki StadiumDates10 August (heats)11 August (semifinals)13 August (final)Competitors47 from 38 nationsWinning time1:43.31Medalists Mohammed Aman Ethiopia (ETH) Nick Symmonds United States (USA) Ayanleh Souleiman Djibouti (DJI)← 20112015 → Official Video Events at the2013 World ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 ...

Ontario Hockey League team in Peterborough Peterborough PetesCityPeterborough, OntarioLeagueOntario Hockey LeagueConferenceEasternDivisionEastFounded1956 (1956)–57Home arenaPeterborough Memorial CentreColoursMaroon, black, cream, white General managerMike OkeHead coachRob WilsonAffiliateLindsay MuskiesWebsitewww.gopetesgo.comFranchise history1951–1954Kitchener Greenshirts1954–1956Kitchener Canucks1956–presentPeterborough PetesChampionshipsPlayoff c...

Palestinian neighborhood in East Jerusalem Wadi Joz Wadi al-Joz (Arabic: وادي الجوز; Hebrew: ואדי אל-ג'וז), also Wadi Joz, is a Palestinian neighborhood in East Jerusalem, located at the head of the Kidron Valley, north of the Old City of Jerusalem. The population of Wadi Joz is 13,000.[1] It is located 750 meters above sea level in the Kidron Valley (Nahal Kidron). Wadi al-Joz, in Arabic, literally means Valley of the Walnuts, though it is believed that the name is ...

Highway in Oklahoma OK 8 redirects here. The term may also refer to Oklahoma's 8th congressional district. State Highway 8OK 8; mainline in red, spur routes in blueRoute informationMaintained by ODOTLength179.1 mi[1] (288.2 km)ExistedAugust 24, 1924–presentMajor junctionsSouth end US 277 / SH-19 in CyrilMajor intersections US 62 / SH-9 in Anadarko US 281 from Anadarko to Watonga I-40 near Hinton US 270 from Geary to Watonga US 6...

クーティ・ウィリアムスCharles Williams クーティ・ウィリアムス(1947年)基本情報出生名 Charles Melvin Williams別名 Cootie Williams生誕 (1911-07-10) 1911年7月10日出身地 アメリカ合衆国 アラバマ州モービル死没 (1985-09-15) 1985年9月15日(74歳没)ジャンル スウィング・ジャズ、ジャンプ・ブルース、R&B職業 作曲家、トランペッター、バンドリーダー担当楽器 トランペット共同作業�...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 花山天皇 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2021年7月) 花山天皇 花山院第65代天皇 在位期間984年9月24日 - ...
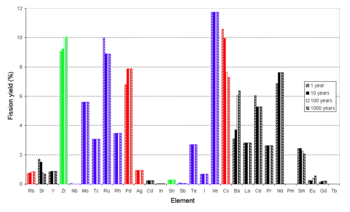
Tendency of highly fluorinated molecules to vaporize Fluoride volatility is the tendency of highly fluorinated molecules to vaporize at comparatively low temperatures. Heptafluorides, hexafluorides and pentafluorides have much lower boiling points than the lower-valence fluorides. Most difluorides and trifluorides have high boiling points, while most tetrafluorides and monofluorides fall in between. The term fluoride volatility is jargon used particularly in the context of separation of radio...





![{\displaystyle I=[0,1]\setminus \mathbb {Q} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f91c1d174ff55213c5e24c70fd61251dafaf42b)
![{\displaystyle T([a_{1},a_{2},\dots ])=[a_{2},a_{3},\dots ].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6639bb7ef1850c0144195a63d59a9869fd8e9616)







![{\displaystyle K_{p}=\lim _{n\to \infty }\left[{\frac {1}{n}}\sum _{k=1}^{n}a_{k}^{p}\right]^{1/p}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/377683fefc4b8aca7bd41a3a9db1a96f2969ea5b)
![{\displaystyle K_{p}=\left[\sum _{k=1}^{\infty }-k^{p}\log _{2}\left(1-{\frac {1}{(k+1)^{2}}}\right)\right]^{1/p}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4995db09406ad5ade0c7377518d44d2c98fae605)



