Élément absorbant

En mathématiques (algèbre), un élément absorbant (ou élément permis) d'un ensemble pour une loi de composition interne est un élément de cet ensemble qui transforme tous les autres éléments en l'élément absorbant lorsqu'il est combiné avec eux par cette loi.

Définition

Soit $(E,\star )$ un magma. Un élément $a$ de $E$ est dit :

absorbant à gauche si $\forall x\in E,\ a\star x=a$ ;
absorbant à droite si $\forall x\in E,\ x\star a=a$ ;
absorbant s'il est absorbant à droite et à gauche.

Propriétés

Dans un magma

Dans un magma $(E,\star )$ $(E,\star )$ , l'élément absorbant, s'il existe :
- est unique : si $a_{1}$ et $a_{2}$ sont deux éléments absorbants, $a_{1}=a_{1}\star a_{2}=a_{2}$ ;
- est idempotent : si $a$ est absorbant, $a\star a=a$ .
Si un magma a un élément absorbant à gauche et un élément absorbant à droite, ces deux éléments sont égaux et le magma a un élément absorbant. En effet, si $a_{1}$ est absorbant à gauche et $a_{2}$ absorbant à droite, alors $a_{1}=a_{1}\star a_{2}=a_{2}$ .
Plusieurs éléments absorbants à gauche ou à droite peuvent exister dans un magma donné, mais s'il existe plus d'un élément absorbant à gauche, il n'en existe aucun à droite. En effet, supposons $a_{1}$ et $a_{2}$ deux éléments absorbants à gauche, et $b$ un élément absorbant à droite: $a_{1}=a_{1}\star b=b=a_{2}\star b=a_{2}$ . Par symétrie, s'il existe plus d'un élément absorbant à droite, il n'en existe aucun à gauche.

Dans un anneau

Dans un anneau (A, +, ×), l'élément neutre 0 de + est absorbant pour ×.

En effet, comme l'élément nul 0 est l'élément neutre de l'addition : $0 = 0 + 0$ .

Ainsi, pour tout élément $a$ de l'anneau $A$ , $a \times0 = a \times(0 + 0)$ .

Par distributivité de la loi × sur la loi +, $a \times(0 + 0) = a \times0 + a \times0$ ,

si bien que $a \times0 = a \times0 + a \times0$ , donc (puisque + est régulière, comme toute loi de groupe)

$a \times0 = 0$

et (de même) :

$0\times a = 0$ .

Exemples

L'élément absorbant de la multiplication entre des nombres réels est le zéro : $a\cdot 0=0\cdot a=0$ (c'est d'ailleurs un exemple d'élément neutre de la première loi de l'anneau, absorbant pour la seconde). De façon analogue, le vecteur nul est élément absorbant pour le produit vectoriel et l'ensemble vide est élément absorbant pour l'intersection d'ensembles.
L'élément absorbant de la disjonction est VRAI et celui de la conjonction est FAUX. Autrement dit, 1 est l'élément absorbant de la fonction OU (ou inclusif) et 0 est l'élément absorbant de la fonction ET.
Dans l'ensemble P(E) des parties d'un ensemble E, l'élément E est absorbant pour la réunion.
Le seul groupe possédant un élément absorbant est le groupe trivial.
Dans l'ensemble des applications de ℝ dans ℝ doté de la loi $(f,g)\mapsto f\circ g$ , les éléments absorbants à gauche sont les fonctions constantes, et il n'existe pas d'élément absorbant à droite.

Voir aussi

Portail de l’algèbre

Read other articles:

Alfred Kinsey

Kinsey tahun 1955 Alfred Charles Kinsey (23 Juni 1894 - 25 Agustus 1956) adalah seorang biolog Amerika Serikat. Ia tertarik di bidang entomologi dan zoologi. Ia terkenal atas penelitian yang dilakukannya pada seksualitas manusia. Penelitiannya berpengaruh luas pada nilai-nilai SosBud di sebagian besar dunia. Penelitiannya juga menjadi titik penting pada revolusi seksual yang terjadi pada tahun 1960-an. Ia menulis beberapa karya yang dikenal sebagai Kinsey Reports. Di dalamnya, ia menanyai dir...

Bola voli di Indonesia

Bola voli di IndonesiaSebuah pertandingan bola voli di Pulau Taliabu, Maluku UtaraNegara IndonesiaBadan yang mengaturPBVSITim nasionalTim nasional putraTim nasional putriPertama kali bermain1928Kompetisi klub Daftar Liga: Proliga Livoli Divisi Utama Livoli Divisi I Piala: Piala Kapolri Kejuaraan: Kejurnas Yunior U-19 Kejurnas U-17 Bagian dari seri tentangBudaya Indonesia Sejarah Sejarah menurut provinsi Bangsa Daftar suku bangsa Daftar suku bangsa menurut provinsi Bahasa Bahasa Indonesia...

Gurans Himal

Gurans HimalSouthern/western aspects of ApiHighest pointPeakApiElevation7,132 m (23,399 ft)Coordinates30°00′15″N 80°56′00″E / 30.00417°N 80.93333°E / 30.00417; 80.93333GeographyGurans Himal CountryNepalParent rangeHimalayas The Gurans Himal is a small subrange of the Himalayas in far western Nepal.[1][2] It is little-known, since it does not contain any 8000 metre peaks, or even any peaks above 7,200 metres. Its highest peak i...

Ferdinando III d'Asburgo

Ferdinando III d'AsburgoFrans Luycx, ritratto dell'imperatore Ferdinando III, 1637 circa; Kunsthistorisches MuseumImperatore Eletto dei RomaniStemma In carica15 febbraio 1637 –2 aprile 1657 Incoronazione18 novembre 1637 PredecessoreFerdinando II SuccessoreLeopoldo I Re d'Ungheria e CroaziaRe di BoemiaIn carica15 febbraio 1637 –2 aprile 1657 Incoronazione8 dicembre 1625 (Ungheria)21 novembre 1627 (Boemia) PredecessoreFerdinando II SuccessoreLeopoldo I Altri titoliRe in Germ...

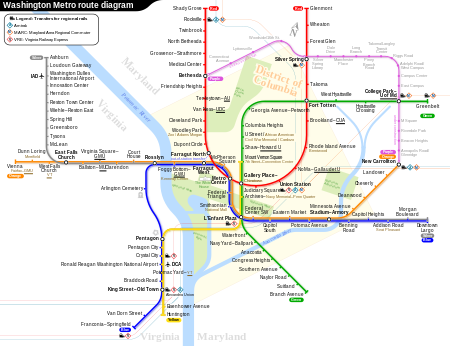
Washington Metro

Washington MetroInfoWilayahWashington, D.C.JenisAngkutan cepatJumlah jalur6Jumlah stasiun91Penumpang harian758.489 (Juni 2013)[1]Penumpang tahunan209 juta (2013, perkiraan)[2]Pimpinan utamaRichard M. SarlesKantor pusat600 5th St NWWashington, D.C. 20001Situs webwww.wmata.comOperasiDimulai27 Maret 1976; 48 tahun lalu (1976-03-27)OperatorWashington Metropolitan Area Transit Authority (WMATA)Jumlah gerbong1.126 rangkaianPanjang kereta6 atau 8 keretaWaktu antara6 menit puncak...

Paul Tillich

German-American theologian and philosopher (1886-1965) Paul TillichBornPaul Johannes Tillich(1886-08-20)August 20, 1886Starzeddel, Province of Brandenburg, Prussia, German EmpireDiedOctober 22, 1965(1965-10-22) (aged 79)Chicago, Illinois, U.S.NationalityGermanAmerican (after 1940)EducationUniversity of BerlinUniversity of TübingenUniversity of Halle-WittenbergUniversity of BreslauNotable workSystematic Theology (1951–1963)The Courage to Be (1952)TitleTheologian and philosopherSpo...

Confessions Part II

2004 single by Usher Confessions Part IISingle by Usherfrom the album Confessions ReleasedJune 1, 2004RecordedJuly 2003GenreR&BLength3:49LabelAristaSongwriter(s)Usher RaymondJermaine DupriBryan-Michael CoxProducer(s)Jermaine DupriBryan-Michael CoxUsher singles chronology Burn (2004) Confessions Part II (2004) My Boo (2004) Music videoConfessions Part II on YouTubeAudioConfessions Part II on YouTubeConfessions Part II Remix on YouTube Confessions Part II is a song by R&B singer Usher, ...

Вавилонские цифры

У этого термина существуют и другие значения, см. Цифра (значения). Вавилонские цифры Системы счисления в культуре Индо-арабская АрабскаяТамильскаяБирманская КхмерскаяЛаосскаяМонгольскаяТайская Восточноазиатские КитайскаяЯпонскаяСучжоуКорейская ВьетнамскаяСчё�...

Bacillus anthracis

Bacillus anthracis Foto mikrograf Bacillus anthracis dari kultur agar dengan pengecatan Fuchsin-biru metilen.PenyakitAntraks Pewarnaan GramGram-positif TaksonomiSuperdomainBiotaDomainBacteriaKerajaanBacillatiFilumBacillotaKelasBacilliOrdoCaryophanalesFamiliBacillaceaeGenusBacillusSpesiesBacillus anthracis lbs Bacillus anthracis merupakan spesies bakteri penyebab antraks—sebuah penyakit yang umum ditemukan pada hewan ternak dan terkadang pada manusia—dan satu-satunya patogen obligat pada g...

Speed Racer

Disambiguazione – Se stai cercando altri significati, vedi Speed Racer (disambigua). Speed RacerUna scena del film.Titolo originaleSpeed Racer Paese di produzioneStati Uniti d'America Anno2008 Durata135 min Rapporto2,39:1 Genereazione RegiaAndy e Larry Wachowski Soggettodalla serie animata di Tatsuo Yoshidastoria di Lana e Lilly Wachowski SceneggiaturaLana e Lilly Wachowski ProduttoreJoel Silver, Lana Wachowski, Lilly Wachowski, Grant Hill Produttore esecutivoDavid Lane Seltzer, Michael La...

Framed (1927 film)

1927 film FramedTheatrical release posterDirected byCharles BrabinScreenplay byMary O'HaraBased onThe Dawn of My Tomorrowby George W. Sutton Jr.StarringMilton SillsNatalie KingstonE. J. RatcliffeCharles K. GerrardEdward Peil Sr.Burr McIntoshCinematographyCharles Van EngerProductioncompanyFirst National PicturesDistributed byFirst National PicturesRelease date June 19, 1927 (1927-06-19) Running time60 minutesCountryUnited StatesLanguageEnglish Framed is a 1927 American drama fil...

Castle of Illusion Starring Mickey Mouse (2013 video game)

2013 video game For the original 1990 game, see Castle of Illusion Starring Mickey Mouse. 2013 video gameCastle of Illusion Starring Mickey MouseDeveloper(s)Sega Studios AustraliaPublisher(s)Sega[a]Composer(s)Shigenori Kamiya, Grant Kirkhope (arranger and additional music)SeriesIllusionPlatform(s)PlayStation 3, Windows, Xbox 360, iOS, Windows Phone, Android, OS XRelease September 3, 2013 PlayStation 3NA: September 3, 2013WW: September 4, 2013Windows, Xbox 360September 4, 2013iOSNovemb...

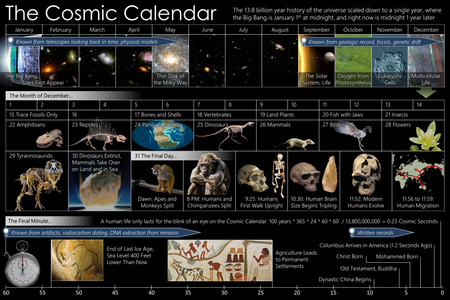
Kalender Kosmik

Kalender Kosmik adalah cara membayangkan luasnya sejarah alam semesta dengan merangkum usianya selama 13,8 miliar tahun menjadi satu tahun saja. Dalam gambaran ini, Ledakan Besar terjadi pada awal 1 Januari dini hari, dan masa kini terangkum pada akhir 31 Desember dini hari.[1] Dalam skala ini, setiap detiknya berarti 438 tahun, setiap jamnya berarti 1,58 juta tahun, dan setiap harinya berarti 37,8 juta tahun. Konsep ini dipopulerkan oleh Carl Sagan dalam bukunya, The Dragons of Eden,...

Leslie Dam

This article is about the dam. For the surrounding locality of the same name, see Leslie Dam, Queensland. Reservoir in west of WarwickLeslie DamLeslie DamLocation11km west of WarwickCoordinates28°13′02″S 151°55′06″E / 28.21722°S 151.91833°E / -28.21722; 151.91833TypeReservoirPrimary outflowsSandy CreekCatchment area603 km2 (233 sq mi)Basin countriesAustraliaSurface area1,288 ha (3,180 acres)Max. depth28.9 m (95 ft)Water vo...

Втрати силових структур внаслідок російського вторгнення в Україну (вересень — грудень 2014)

Докладніше: Втрати силових структур внаслідок російського вторгнення в Україну У статті наведено список втрат силових структур України у російсько-українській війні з 1 вересня по 31 грудня 2014 року (включно). Зміст 1 Список загиблих 1 вересня — 31 грудня 2014 року 1.1 Вересен...

Diritto latino

L'anfiteatro di Casinum, nel Latium adiectum, attuale Cassino. Definita da Strabone l'ultima città latina (Geografia), nel suo territorio fu stabilita una colonia latina. Il diritto latino (latino ius Latii o Latinitas o Latium) era uno status civile che in epoca romana si situava a livello intermedio tra la piena cittadinanza romana e lo stato di non cittadino (peregrinus). Il diritto latino, noto anche come cittadinanza latina, era un insieme di diritti legali originariamente concessi ai l...

Godflesh

English industrial metal band This article is about the band. For their self-titled extended play, see Godflesh (EP). GodfleshGodflesh performing on 22 April 2014: B. C. Green and Justin BroadrickBackground informationAlso known asO.P.D. (1982–1983)Fall of Because (1983–1987)OriginBirmingham, EnglandGenres Industrial metal post-metal experimental metal Years active1988–2002, 2009–presentLabels Swordfish Earache Columbia Avalanche Music for Nations Koch Relapse Members Justin Broadrick...

Suomenlinna

Questa voce o sezione sugli argomenti isole e Norvegia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. SuomenlinnaVeduta aerea delle isoleGeografia fisicaCoordinate60°08′37″N 24°59′04″E60°08′37″N, 24°59′04″E Geografia politicaStato Finlandia CartografiaSuomenlinna voci di isole de...

柳州轨道交通

柳州轨道交通，是广西壮族自治区柳州市规划建设中的城市轨道交通系统，采用跨座式单轨列车，规划由1号线、1号线支线、2号线、3号线、4号线、市郊S1线、市郊S2线、市郊S3线组成[1]，其中S1号线利用柳州火车站至鹿寨火车站原有的闲置铁路建设。[2] 历史中华民国大陆时期，柳州曾于1928年3月开工一条轻便铁路，这条轨道有两条支线：一是经东大路至柳州砖厂�...

Vallecas

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Vallecas» – noticias · libros · académico · imágenesEste aviso fue puesto el 7 de octubre de 2014. Vallecas Municipio desaparecido Escudo VallecasLocalización de Vallecas en Comunidad de Madrid Ubicación de VallecasCoordenadas 40°23′00″N 3°37′00″O / 40.383333333333, -3.6166666666667Entidad Municipio desaparecido • País Es...

Saint Paul's Church, Tarsus

/profillengkap.com/index.php/article/John Copley, 1st Baron Lyndhurst

List of football stadiums in France

Template talk:Footer Olympic Champions 200 m Freestyle Men

1989 Sovran Bank Classic – Singles

KNVB Amateur Cup

Cidatar, Cisurupan, Garut