Vicomté de Caen
|
Read other articles:

Draw G's First BreathAlbum mini karya G.NADirilis14 Juli 2010Direkam2010GenreK-pop, pop, R&BDurasi17:24BahasaKoreaLabelCube Entertainment, Universal Music GroupKronologi G.NA Draw G's First Breath(2010) Black & White (2011)Black & White2011 Singel dalam album Draw G's First Breath Thing I'd Like to Do With My LoverDirilis: 5 Juli 2010 I'll Back Off So You Can Live BetterDirilis: 14 Juli 2010 Supa' SoloDirilis: Agustus 2010 Draw G's First Breath adalah album mini pertama pe...

Ediakara~635 – 538.8 ± 0.2 Ma Had'n Arkean Proterozoikum Pha. Peta dunia pada Ediakara Akhir.EtimologiNama resmiFormalNama ratifikasi1990Informasi penggunaanBenda angkasaBumiPenggunaan regionalGlobal (ICS)Skala waktuICS Time ScaleRentang waktuSatuan kronologisPeriodeSatuan stratigrafikSistemJangka waktu resmiFormalAmbang batas jangka waktu Bawah Karbonat tutup yang berbeda di seluruh dunia. Permulaan dari pola khas perubahan sekuler dalam isotop karbon. Versi GSSPBagian Enorama Creek, Flin...

Novi Rubadi Sugito Kepala Staf Divisi Infanteri 1/KostradPetahanaMulai menjabat 27 April 2023 PendahuluJonathan Binsar Parluhutan SianiparPenggantiPetahanaPa Sahli Kasad Tk. II Bidang SosbudMasa jabatan16 Januari 2023 – 27 April 2023 PendahuluAlrizalPenggantiJuinta Omboh SembiringKomandan Korem 152/BabullahMasa jabatan12 Agustus 2021 – 18 Januari 2023 PendahuluImam Sampurno SetiawanPenggantiElkines Villando Dewangga Kusumawide Informasi pribadiLahir25 November 1970 (...

Vale Tudo MMA events 1994–2013 Vale Tudo JapanNative nameヴァーリ・トゥード・ジャパンIndustryMixed martial arts promotionFoundedJapan (1994 (1994))FounderSatoru SayamaParentShooto (1994-1999)Vale Tudo Japan Executive Committee (2009-Present)Websitehttp://www.valetudojapan.com/Vale Tudo Japan (VTJ) (Japanese: ヴァーリ・トゥード・ジャパン, Hepburn: Vāri Tūdo Japan) is an annual mixed martial arts competition held in Japan. Originally arranged by promoter and...

Biara Ivolga. Wilayah-wilayah di Rusia dengan mayoritas Buddha. Dalam sejarah, agama Buddha masuk ke tanah Rusia pada awal abad ke-17.[1][2] Agama Buddha dianggap sebagai salah satu agama tradisional di Rusia, yang secara sah menjadi bagian dari warisan sejarah Rusia.[3] Selain tradisi kebiaraan bersejarah dari Buryatia, Kalmykia dan Tuva, agama Buddha sekarang menyebar ke seluruh Rusia, dengan beberapa orang beretnis Rusia yang masuk ke agama tersebut.[4] Bent...

روبرت لانغدون (بالإنجليزية: Robert Langdon) روبرت لانغدون كما جسده توم هانكس في فيلم ملائكة وشياطين معلومات شخصية الميلاد 22 يونيو 1964 (60 سنة) مواطنة الولايات المتحدة أقرباء هاورد لانغدون (جد) عائلة والد لم يُذكر إسمه (متوفى) الحياة العملية أول ظهور ملائكة وشياطين المبتك�...

Ariella CalistaLahirAriella Calista12 Mei 2000 (umur 23)Jakarta, IndonesiaPendidikanSMP Kristen Ketapang 1, SMA Kristen Ketapang 1AlmamaterUniversitas Atma Jaya JakartaPekerjaanModelPenyanyiAktrisPenariSuami/istriWelly Surya (m. 2023)KerabatEve Antoinette Ichwan (adik)Karier musikGenrePopInstrumenVokal, biolaTahun aktif2008–sekarangArtis terkaitJKT48Mantan anggotaJKT48 (2018–2022)Situs webJKT48 Ariella Calista Ichwan (lahir 12 Mei 2000) adalah salah se...

Sports shooting at the Olympics Shootingat the Games of the XXVIII OlympiadVenueMarkopoulo Olympic Shooting CentreDates9–17 August 2004Competitors390 from 103 nations← 20002008 → Shooting at the2004 Summer OlympicsQualificationRifle50 m rifle three positionsmenwomen50 m rifle pronemen10 m air riflemenwomenPistol50 m pistolmen25 m pistolwomen25 m rapid fire pistolmen10 m air pistolmenwomenShotgunTrapmenwomenDouble trapmenwomenSkeetmenwomenRunning target10 m ru...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2020) (Learn how and when to remove this message) You can help expand this article with text translated from the corresponding article in German. (October 2020) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like De...

منى سيمبسون معلومات شخصية اسم الولادة منى سيمبسون الميلاد 14 يونيو 1957 (العمر 66 سنة)الولايات المتحدة الجنسية الأمريكية العرق عربية.[1] الأولاد 2 الأب عبد الفتاح جندلي [لغات أخرى] إخوة وأخوات ستيف جوبز أقرباء ستيف جوبز (أخ) الحياة العملية النوع الأدب الأمري�...

College of University of Oxford Keble CollegeUniversity of OxfordArms: Argent, a chevron engrailed gules, on a chief azure, three mullets pierced or LocationParks Road, Oxford OX1 3PGCoordinates51°45′32″N 1°15′28″W / 51.758899°N 1.257715°W / 51.758899; -1.257715Latin nameCollegium KeblenseMottoPlain living and high thinking[1]Established1870 (1870)Named forJo...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: SV Grödig – news · newspapers · books · scholar · JSTOR (October 2022) (Learn how and when to remove this ...

Artikel utama: Toyota Corona Toyota Corona AbsoluteInformasiJuga disebutToyota Corona ExsiorToyota Carina EMasa produksiMar 1992[butuh rujukan]—1998[butuh rujukan]PerakitanToyota City, JapanBurnaston, Derbyshire, EnglandThames, New ZealandJakarta, IndonesiaSanta Rosa City, Laguna, PhilippinesBodi & rangkaBentuk kerangka4-pintu sedan5-pintu liftback5-pintu station wagonTata letakFR layoutFF layoutMobil terkaitToyota CaldinaToyota CelicaToyota CurrenToyota Carina...

Oud-Heverlee LeuvenCalcio Segni distintiviUniformi di gara Casa Trasferta Colori sociali Bianco, rosso, verde InnoT Spel Van OHLFrère Sous Rire Dati societariCittàLovanio Nazione Belgio ConfederazioneUEFA Federazione URBSFA/KBVB CampionatoPro League Fondazione2002 Proprietario King Power Presidente Aiyawatt Srivaddhanaprabha Allenatore Óscar García Junyent StadioDen Dreef(10 000 posti) Sito webohleuven.com Palmarès Stagione in corso Dati aggiornati al 3 settembre 2021Si inv...

Hughes Aircraft CompanyLogo Stato Stati Uniti Fondazione1932 Fondata daHoward Hughes Chiusura1997 Sede principaleCulver City GruppoRaytheon Company Settoreaeronauticoaerospazialedifesa Prodottiaerei civili e militarisistemi d'arma Modifica dati su Wikidata · Manuale La Hughes Aircraft Company è stata una società aerospaziale e un'industria della difesa statunitense fondata nel 1932 dal regista e produttore cinematografico, nonché appassionato aviatore, Howard Hughes. La sede del...

Indian writer and activist Manoranjan Byapariমনোরঞ্জন ব্যাপারীMember of the West Bengal Legislative AssemblyIncumbentAssumed office 02 May 2021Preceded byAshim Kumar MajhiConstituencyBalagarhChairperson of West Bengal Dalit Sahitya AcademyIncumbentAssumed office 14 Sep 2020 Personal detailsBornc. 1950–51[1]Pirojpur, East Bengal, Dominion of PakistanNationalityIndianPolitical partyAll India Trinamool CongressOther politicalaffiliationsNaxalites...

This article is about the Canadian governor. For the Crown Governor of Virginia, see John Harvey (Virginia governor). For other people, see John Harvey. Sir John Harvey Lieutenant-General Sir John Harvey, KCB KCH (23 April 1778 – 22 March 1852) was a British Army officer and a lieutenant governor. He was commissioned into the 80th Foot in 1794 and served in several different locations, including France, Egypt, and India. He came to Canada in 1813 and served as a lieutenant colonel i...

Book by Ludwig Bemelmans Madeline's Rescue First editionAuthorLudwig BemelmansIllustratorLudwig BemelmansCover artistUrpatzGenreChildren's bookPublisherViking PressPublication date1953Publication placeUnited States Madeline's Rescue is a children's picture book by Ludwig Bemelmans, the second in his Madeline series. Released by Viking Press, it was the recipient of the Caldecott Medal for illustration in 1954.[1] Plot Madeline falls into the Seine River one day and is saved by a ...

SAE1 بنى متوفرة بنك بيانات البروتينOrtholog search: PDBe RCSB قائمة رموز معرفات بنك بيانات البروتين 1Y8Q, 1Y8R, 3KYC, 3KYD معرفات أسماء بديلة SAE1, AOS1, HSPC140, SUA1, UBLE1A, SUMO1 activating enzyme subunit 1 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 613294 MGI: MGI:1929264 HomoloGene: 4019 GeneCards: 10055 علم الوجود الجيني وظائف جزيئية...
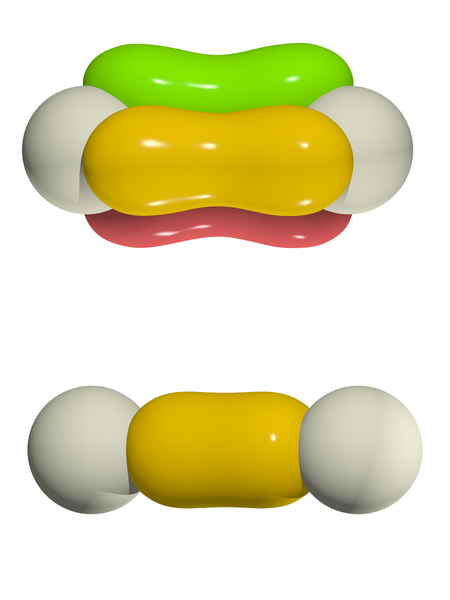
Wannier functions of triple- and single-bonded nitrogen dimers in palladium nitride. The Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier in 1937.[1][2] Wannier functions are the localized molecular orbitals of crystalline systems. The Wannier functions for different lattice sites in a crystal are orthogonal, allowing a convenient basis for the expansion of electron states in certain regimes. Wann...