Transformation inverse de Laplace
|
Read other articles:

2006 video by TripodPod August NightVideo by TripodReleased2006-03-24Recorded2005-08-25GenreComedyLengthApprox 70 minsLabelLiberation Music Tripod: Pod August Night (commonly abbreviated PAN) is a DVD recording of the last performance of 'The Triumphant Return of Pod August Nights' by the Australian comedy act Tripod. The performance occurred at the Northcote Social Club in Northcote, Victoria, on 25 August 2005. The DVD includes extras such as additional footage from the show under ...

Halaman ini sedang dipersiapkan dan dikembangkan sehingga mungkin terjadi perubahan besar.Anda dapat membantu dalam penyuntingan halaman ini. Halaman ini terakhir disunting oleh DayakSibiriak (Kontrib • Log) 1 hari 216 menit lalu. Jika Anda melihat halaman ini tidak disunting dalam beberapa hari, mohon hapus templat ini. Artikel ini adalah bagian dari seriPolitik dan ketatanegaraanIndonesia Pemerintahan pusat Hukum Pancasila(ideologi nasional) Undang-Undang Dasar Negara Republik Indonesia T...

Нир-Давид в 1940 году Стена и башня (ивр. חומה ומגדל — Хома́ у-мигда́ль) — тактика строительства поселений в подмандатной Палестине, применявшаяся еврейским населением страны в период арабского восстания 1936—1939 годов. Появление такой тактики было вызвано действи�...

Village in Illinois, United StatesGiffordVillageA picture of Gifford's Main StreetMotto: America's HometownGiffordLocation within Champaign CountyShow map of Champaign County, IllinoisGiffordGifford (Illinois)Show map of IllinoisCoordinates: 40°18′28″N 88°01′17″W / 40.30778°N 88.02139°W / 40.30778; -88.02139CountryUnited StatesStateIllinoisCountyChampaignGovernment • Village presidentAdam Pannbacker[citation needed]Area[1]&...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Eksplorasi geofisika – berita · surat kabar · buku · cendekiawan · JSTOR Eksplorasi geofisika adalah kegiatan penjajakan struktur geologi yang cocok bagi pengumpulan minyak bumi dengan menggunakan perala...

Artikel ini berisi konten yang ditulis dengan gaya sebuah iklan. Bantulah memperbaiki artikel ini dengan menghapus konten yang dianggap sebagai spam dan pranala luar yang tidak sesuai, dan tambahkan konten ensiklopedis yang ditulis dari sudut pandang netral dan sesuai dengan kebijakan Wikipedia. (Juni 2018) Allen & Overy LLPMarkasOne Bishops Square, London, Inggris E1 6ADBritania RayaCabang44 di 31 negaraPengacara Rekan: sekitar 554 Advokat: sekitar 2.768[1] Karyawansekitar 5...

Wikipedia bahasa Sunda URLsu.wikipedia.orgTipeEnsiklopedia daringPerdagangan ?TidakRegistrationOpsionalLangueBahasa SundaLisensiCreative Commons Atribusi-BerbagiSerupa 3.0 Tanpa Adaptasi dan Lisensi Dokumentasi Bebas GNU PemilikYayasan WikimediaService entry15 Maret 2004 Wikipedia bahasa Sunda adalah ensiklopedia dari versi bahasa Sunda Wikipedia. Wikipedia bahasa Sunda umumnya mengikuti peraturan-peraturan dasar Wikipedia bahasa Indonesia. Pranala luar Wikipedia bahasa Sunda lbsDaftar ...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

Senegalese footballer Malick Mané Mané playing for Sandefjord in 2008Personal informationFull name Malick Neme ManéDate of birth (1988-10-14) 14 October 1988 (age 35)Place of birth Ziguinchor, SenegalHeight 1.73 m (5 ft 8 in)Position(s) Forward, wingerYouth career0000–2005 Casa SportsSenior career*Years Team Apps (Gls)2005–2007 Casa Sports 2008–2011 Sandefjord 82 (19)2011 → Aktobe (loan) 29 (12)2012–2014 Sogndal 59 (12)2014–2015 IFK Göteborg 11 (1)2014 → ...
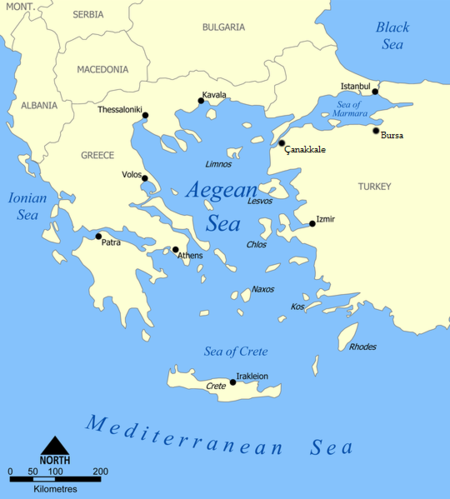
Questa voce sugli argomenti geografia della Grecia e mari è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Mar di CretaLa costa del mar di Creta nei pressi di CandiaParte diMar Mediterraneo Stato Grecia PeriferiaAttica, Creta, Egeo meridionale, Peloponneso Coordinate36°N 25°E / 36°N 25°E36; 25Coordinate: 36°N 25°E / 36°N 25°E36; 25 IdrografiaIsoleAnafi, Caso, Cerigo, Cerigotto, Creta, Milo, Policandro, Santo...

Mobil Eisenacher Motoren Werke yang dirilis pada tahun 1941. Eisenacher Motorenwerk (EMW) adalah produsen otomotif dari Jerman Timur dengan produksi mobil dan sepeda motor yang berbasis di Eisenach. EMW juga mengadakan sempat turun di ajang Formula Satu sebagai konstruktor pada tahun 1953, tetapi berpartisipasi hanya dalam satu balapan saja, yaitu Jerman 1953. lbsKonstruktor Formula SatuMusim 2024 Alpine Aston Martin Ferrari Haas McLaren Mercedes RB Red Bull Sauber Williams Mantan AFM AGS Alf...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Lucretia, digravir oleh Raimondi setelah dirancang oleh Raffaello Sanzio. Marcantonio Raimondi, sering disebut hanya Marcantonio (skt. 1470/82 – skt. 1534),[1] merupakan seorang pematung berkebangsaan Italia, yang dikenal sebagai juru gambar ...

French admiral (1796–1864) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ferdinand-Alphonse Hamelin – news · newspapers · books · scholar · JSTOR (August 2019) (Learn how and when to remove this message) Ferdinand Alphonse HamelinBorn(1796-09-02)2 September 1796Pont-l'Évêque, Calvados, Normandy, France...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Reed Switch adalah saklar listrik dioperasikan oleh medan magnet. Ini diciptakan di Bell Telephone Laboratories pada tahun 1936 oleh WB Ellwood. Contoh aplikasi Reed Switch adalah untuk mendeteksi pembukaan pintu, bila digunakan sebagai saklar jarak u...

Toko mi soba toshikoshi Toshikoshi soba (年越し蕎麦code: ja is deprecated ), atau sering dikenali dengan mi pergantian tahun, adalah hidangan mi tradisional Jepang yang dimakan pada Malam Tahun Baru. Kebiasaan ini dipercaya dapat melepaskan kesulitan karena sifat mi soba yang mudah dipotong ketika dimakan.[1] Sejarah Adat yang berbeda dari daerah ke daerah di Jepang menyebabkan hidangan ini juga disebut misoka soba, tsugomori soba, kure soba, jyumyo soba, fuku soba, dan unki soba...

Ministry of Public Works and TransportAgency overviewFormed1962Agency executiveKamel BeldjoudWebsitehttps://portail.mtpt.gov.dz The Ministry of Public Works and Transport (French: Ministère des Travaux Publics et des Transports), formerly the Transport Ministry[1] (Arabic: وزارة اﻟﻨﻘﻞ, French: Ministère des Transports) is a government ministry of Algeria. Its head office is in El Biar, Algiers.[2] The Directorate of Civil Aviation and Meteorology (DACM, French:...

Iglesia de NuestraSeñora del Manzano Bien de Interés Cultural (25 de abril de 1974) (RI-51-0003934) Patrimonio de la Humanidad (elemento asociado de «Caminos de Santiago de Compostela: Camino Francés y Caminos del Norte de España», n.º ref. 669bis) (2015) LocalizaciónPaís España EspañaComunidad Castilla y León Castilla y LeónProvincia Burgos BurgosLocalidad CastrojerizCoordenadas 42°17′34″N 4°07′40″O / 42.29277778, -4.12777778Informa...

275th Rifle DivisionActive 1st formation: July 1941 – December 1942 2nd formation: July 1943 – late 1945 Country Soviet UnionBranch Red ArmyTypeRifle divisionEngagementsWorld War IIBattle honours Khingan (2nd formation) Military unit The 275th Rifle Division (Russian: 275-я стрелковая дивизия) was an infantry division of the Soviet Union's Red Army during World War II, formed twice. The division was first formed in the summer of 1941 and was destroyed in the No...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is missing information about the film's production. Please expand the article to include this information. Further details may exist on the talk page. (December 2017) This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all im...

ميّز عن عدسة مكبرة. مجموعة من العدسات المقربة العدسة المقربة في مجال التصوير الضوئي والتصوير السينمائي هي عدسة خاص من العدسات طويلة البعد البؤري يكون فيها الطول الفيزيائي للعدسة أقصر من البعد البؤري.[1] وبذلك يمكن لهذه العدسات أن تقوم بالتقريب بشكل مناظر للمقراب...









![{\displaystyle f(t)={\frac {\exp(ct)}{t_{\max }}}\left[{\frac {F(c)}{2}}+\sum _{k=1}^{\infty }(\Re [F(c+j\omega _{k})]\cos(\omega _{k}t)-\Im [F(c+j\omega _{k})]\sin(\omega _{k}t))\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60cef9880460fe4e53dea053c4d3cc8cdbc96a13)



![{\displaystyle {\begin{array}{cccc}g:&\left]0;+\infty \right[&\longrightarrow &\mathbb {R} \\&s&\longmapsto &\displaystyle {\int _{0}^{+\infty }f(u){\rm {e}}^{-su}{\rm {d}}u}\end{array}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fccd36ff87a2c738ffa4988e59ca5679d77ebce6)







