Transformation de Bäcklund
|
Read other articles:

Sebuah kolek Kolek pengaman. Kolek adalah sejenis perahu kecil, yang sering dibawa atau ditarik oleh kapal yang lebih besar untuk digunakan sebagai perahu layan . [1] Kolek utilitas biasanya berupa perahu dayung atau memiliki motor tempel . Beberapa di antaranya dilengkapi untuk berlayar tetapi berbeda dengan kolek layar, yang dirancang pertama dan terutama untuk berlayar. Kegunaan utama kolek adalah untuk berpindah dari kapal yang lebih besar, terutama bila kapal yang lebih besar tid...

Wangsa Wettin adalah dinasti bangsawan yang selama lebih dari 800 tahun pernah menguasai dan memerintah wilayah yang sekarang menjadi negara bagian Sachsen, Jerman. Anggota dari wangsa ini juga selama beberapa waktu juga pernah menjadi penguasa Polandia. Jika dirunut lebih jauh, keturunan wangsa Wettin pada masa-masa yang berbeda pernah menduduki takhta Britania Raya, Portugal, Bulgaria, Polandia, Sachsen, dan Belgia. Dari semua negara-negara ini, hanya keturunan di Britania (dari cabang Sac...

Untuk kegunaan lain, lihat Babun (disambiguasi). Babun[1] Babun anubis Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mamalia Ordo: Primata Famili: Cercopithecidae Subfamili: Cercopithecinae Tribus: Papionini Genus: PapioErxleben, 1777 Spesies tipe Simia hamadryasLinnaeus, 1758 Spesies Papio hamadryas Papio papio Papio anubis Papio cynocephalus Papio ursinus Sinonim Chaeropitheus Gervais, 1839 Comopithecus J. A. Allen, 1925 Cynocephalus G. Cuvier and É. Geoffroy, 1795 H...
This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Płock Voivodeship 1975–1998 – news · newspapers · books · scholar · JSTOR (August 2009) (Learn how and when to remove this template message) Płock Voivodeship (Polish: województwo płockie) was a unit of administrative division and local government in Poland from 1975 ...

Entry for Iceland in ISO 3166-2 ISO 3166-2:IS is the entry for Iceland in ISO 3166-2, part of the ISO 3166 standard published by the International Organization for Standardization (ISO), which defines codes for the names of the principal subdivisions (e.g., provinces or states) of all countries coded in ISO 3166-1. Currently for Iceland, ISO 3166-2 codes are defined for 8 regions and 64 municipalities. Each code consists of two parts, separated by a hyphen. The first part is IS, the ISO 3166-...

Ярусоло́в, или я́русник, — рыболовное судно, предназначенное для морского ярусного лова рыбы и других гидробионтов (например, кальмаров и крабов). Океанские ярусоловы оснащаются механизированными или автоматизированными (автолайн) линиями постановки и выборки ярусо...

Patung Tanit yang ditemukan di Nekropolis Puig des Molins dari abad ke-4 SM, kini disimpan di Museum Puig des Molins di Ibiza, Spanyol Tanit adalah seorang dewi dalam kepercayaan Fenisia dan Kartago. Ia merupakan dewi utama Kartago bersama dengan pasangannya, Baal-hamon.[1][2] Suku Berber kemudian juga ikut memuja Tanit. Tanit juga disebut Tinnit, Tannou, atau Tangou. Nama ini tampaknya berasal dari Kartago meskipun tidak ditemukan di dalam nama teoforis setempat.[3] P...
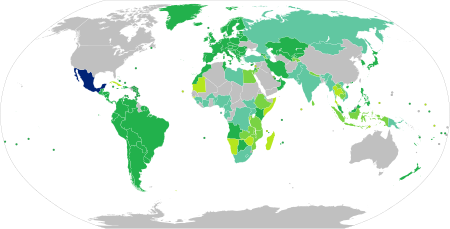
Administrative entry restrictions A Mexican passport Visa requirements for Mexican citizens are administrative entry restrictions by the authorities of other states placed on citizens of Mexico As of 2024, Mexican citizens had visa-free or visa on arrival access to 161 countries and territories, ranking the Mexican passport 23rd in the world according to the Henley Passport Index.[1] Visa requirements map Visa requirements for Mexican citizens holding ordinary passports Me...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Le terme « achenau » est également utilisé dans le pays Royannais pour les différents bras d'eau qui relient les marais aux rivières ou fleuves comme la Seudre. l'Acheneau Le château de Granville à Port-Saint-Père depuis le pont sur l'Acheneau. Cours de l’Acheneau. Caractéristiques Longueur 29,8 km [1] Bassin collecteur la Loire Régime pluvial océanique Cours Origine Lac de Grand-Lieu · Localisation Saint-Philbert-de-Grand-Lieu · Altitude 3 m · Coordonné...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2016) الطري�...

Рельеф дна Северного ледовитого океана Континентальный шельф Российской Федерации (также называемый Российский континентальный шельф) геологически определяется как весь континентальный шельф, примыкающий к побережью России. В международном же праве Конвенция ООН по ...

Gathering of members of both houses of Congress Joint session of the United States CongressSeal of the United States CongressHistoryFoundedMarch 4, 1789(235 years ago) (1789-03-04)LeadershipSpeaker of the HouseMike Johnson (R) since October 25, 2023 President of the SenateKamala Harris (D) since January 20, 2021 StructureSeats535 voting members 100 senators 435 representatives 6 non-voting membersSenate political groups Democratic (48) Independent (3)[a]&...

2020 US federal law; Phase 3.5 of fiscal COVID-19 pandemic relief Paycheck Protection Program and Health Care Enhancement ActLong titleMaking appropriations for the Department of the Interior, environment, and related agencies for the fiscal year ending September 30, 2019, and for other purposes.NicknamesAdditional Emergency Appropriations for Coronavirus ResponseEnacted bythe 116th United States CongressEffectiveApril 24, 2020CitationsPublic lawPub. L.Tooltip Public Law (United States)&...

Arcade entertainment machine For other uses, see Pinball (disambiguation). The article's lead section may need to be rewritten. Please help improve the lead and read the lead layout guide. (May 2023) (Learn how and when to remove this message) Terminator 2: Judgment Day, 1991 pinball machine designed by Steve Ritchie A self-made pinball game in Niger Pinball (originally called pintable in the UK[1]) games are a family of games in which a ball is propelled into a specially designed tab...

Lazzaro de' Taldi Lazzaro de' Taldi (1399 – 1452) è stato un pittore italiano. Lazzaro Vasari, o più propriamente come Lazzaro Taldi e come Lazzaro di Niccolò de' Taldi, fu un pittore italiano nato in provincia di Arezzo e fu il bisnonno del più celebre pittore e storico dell'arte Giorgio Vasari. Proprio nelle Vite di Giorgio, vengono narrati alcuni particolari significativi della vicenda umana ed artistica dell'antenato: apprendiamo che fu amico di Piero della Francesca, col quale coll...
Ảnh chụp màn hình trò chơi Edge được mô phỏng lại trên điện thoại di động Sony Ericsson W880i Trò chơi điện tử Các nền tảng Trò chơi arcade Trò chơi console Máy console Máy chơi trò chơi điện tử tại gia Máy chơi trò chơi điện tử cầm tay Trò chơi điện tử Trò chơi âm thanh Trò chơi điện tử cầm tay Trò chơi trực tuyến Webgame Trò chơi mạng xã hội Trò chơi di động PC Linux Mac Trò chơi thực ...

Marriott International Création 8 octobre 1993[1] Fondateurs J. Willard Marriott Forme juridique Société du Delaware (d) Action NASDAQ (MAR) Siège social Bethesda États-Unis Activité Hôtellerie-restauration et industrie du tourisme (d) Produits Hôtel, domaine touristique et franchise Filiales Delta Hotels (en) (depuis le 1er avril 2015)[2],[3]Westin Hotels & Resorts (depuis 2016)Starwood Hotels & Resorts WorldwideSheraton Hotels & ResortsResidence Inn by Marriott (en...

Cet article est une ébauche concernant une localité tchèque. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Bezkov Chapelle à Bezkov. Administration Pays Tchéquie Région Moravie-du-Sud District Znojmo Région historique Moravie Maire Jiří Tunka Code postal 339 02 Indicatif téléphonique international +(420) Démographie Population 212 hab. (2020) Densité 38 hab./km2 Géographie Coordo...

テレビ番組・中継内での各種情報(終了した番組・中継を含みます)は、DVDやBlu-rayなどでの販売や公式なネット配信、または信頼できる紙媒体またはウェブ媒体が紹介するまで、出典として用いないで下さい。 検証可能性に基づき除去される場合があります。 この記事には、過剰に詳細な記述が含まれているおそれがあります。百科事典に相応しくない内容の増大は�...







