Totipotence

La totipotence, énoncée en 1902 par Gottlieb Haberlandt, est, en biologie, la capacité d’une cellule à se différencier en n’importe quelle cellule spécialisée et de se structurer en formant un être vivant multicellulaire[1]. Elle peut ainsi permettre de reconstituer un organisme au complet à partir d'une cellule. La totipotence a un spectre plus large que la pluripotence, la multipotence, et l'unipotence.

Biologie

Ranunculus asiaticus exemple de totipotence de deux individus MHNT

Chez les mammifères, l'ovocyte fécondé et chaque cellule fille (blastomère) de l'embryon pendant les toutes premières divisions cellulaires sont les seules vraies cellules totipotentes. Pour l'être humain, la totipotence des blastomères de l'embryon à deux ou à quatre cellules est attestée par les naissances de jumeaux monozygotes et de quadruplés monozygotes[2],[3].

Il ne faut pas confondre les propriétés de potence (pluripotence, multipotence, unipotence) avec la notion de cellules souches, dont la capacité est l'auto-renouvellement et son maintien dans cet état.

Chez la plupart des animaux, la propriété de totipotence est perdue très rapidement in vivo au cours des premières divisions cellulaires. Les cellules totipotentes ne s'auto-renouvellent donc pas mais se différencient vers le trophoblaste et la masse cellulaire interne du blastocyste. Il existe néanmoins des protocoles permettant de maintenir en culture in vitro les cellules pluripotentes (par exemple les cellules souches embryonnaires).

Les cellules végétales peu spécialisées sont totipotentes. C'est le cas par exemple des méristèmes et des jeunes cellules qu'ils ont produites, les cellules de parenchyme, les jeunes cellules de la moelle, les cellules compagnes des tubes criblés mais pas ces derniers. Dans le cas du greffage, dans un premier temps, ce sont essentiellement les cellules du parenchyme qui, en se dédifférenciant sous le contrôle du facteur de transcription WIND1, produiront un cal, c'est-à-dire amas de cellules indifférenciées et totipotentes.

L'espèce Kalanchoe pinnata a la particularité d'être particulièrement efficace pour se reproduire. Des centaines de cellules de ses bords de feuilles donnent naissances à des plantules qui peuvent facilement se séparer et donner de nouvelles plantes[4].

Notes et références

  1. ↑ (en) Robin Lovell-Badge, « Many ways to pluripotency », Nature Biotechnology, vol. 25, no 10,‎ , p. 1114–1111 (PMID 17921995, DOI 10.1038/nbt1007-1114).
  2. ↑ (en) Allan F. Mirsky, Linas A. Bieliauskas, Louis M. French, Daniel P. Van Kammen, Erik Jönsson et Göran Sedvall, « A 39-Year Followup of the Genain Quadruplets », Schizophrenia Bulletin (en), vol. 26, no 3,‎ , p. 699–708 (PMID 10993407, DOI 10.1093/oxfordjournals.schbul.a033487).
  3. ↑ (en) Gary Steinman, « Spontaneous Monozygotic Quadruplet Pregnancy : An Obstetric Rarity », Obstetrics & Gynecology, vol. 91, no 5 Pt 2,‎ , p. 866 (PMID 9572198, lire en ligne).
  4. ↑ Valentin Hammoudi, Le pouvoir des plantes, Paris, Editions humenSciences, , 250 p. (ISBN 979-1-0403-0015-1), p. 192

Articles connexes

Read other articles:

The Gap (Sydney)

Ocean cliff on the South head of Sydney Harbour, New South Wales, Australia Looking north towards high cliffs that create The Gap near Watsons Bay The Gap is an ocean cliff at South Head in the Eastern Suburbs of Sydney, Australia. The area, which faces the Tasman Sea, is located in the suburb of Watsons Bay. Although the cliff is a popular tourist destination, it has infamy for suicides. History A tram passing through The Gap on its way to Watsons Bay, c. 1949. Prior to European colonisation...

 

Lambert Hillyer

American film director Lambert HillyerBornLambert Harwood Hillyer(1893-07-08)July 8, 1893Tyner, IndianaDiedJuly 5, 1969(1969-07-05) (aged 75)Los Angeles, CaliforniaOccupation(s)Film director, screenwriterYears active1917–1949 Lambert Harwood Hillyer (July 8, 1893 – July 5, 1969) was an American film director and screenwriter. Biography Lambert Harwood Hillyer was born July 8, 1893, in Tyner, Indiana.[1] His mother was character actress Lydia Knott.[2] A gradu...

 

Buku kegiatan

Contoh buku kegiatan. Buku kegiatan atau buku aktivitas adalah sejenis buku yang umumnya ditujukan untuk anak-anak, yang berisi kandungan interaktif seperti permainan, teka-teki, kuis, gambar untuk diwarnai, dan unsur-unsur lain yang melibatkan menulis atau menggambar dalam buku itu sendiri. Buku ini mungkin mempunyai naratif yang longgar atau berisi unsur bukan interaktif lain yang terstruktur di sekitar unsur interaktif. Buku kegiatan dapat dibuat untuk hiburan, pendidikan, atau campuran ke...

FC Akhmat Grozny

Russian football club For other uses, see Terek (disambiguation). Football clubAkhmat GroznyFull nameРеспубликанский футбольный клуб «Ахмат»Republican Football ClubAkhmatFounded1946; 78 years ago (1946)GroundAkhmat ArenaCapacity30,597General directorMagomed DaudovHead coachMiroslav RomaschenkoLeagueRussian Premier League2022–23Russian Premier League, 5th of 16WebsiteClub website Home colours Away colours Current season Republican Footbal...

 

Hold Your Breath (2012 film)

2012 American filmHold Your BreathDirected byJared CohnScreenplay byGeoff MeedStory byKenny ZinnProduced byDavid Michael LattDavid RimawiPaul BalesStarringKatrina BowdenRandy WayneCinematographyStuart BreretonEdited byBobby K. RichardsonMusic byChris RidenhourProductioncompaniesGlobal AsylumTransformation FilmsDistributed byThe Asylum ProductionsRelease date October 5, 2012 (2012-10-05) (United States) Running time90 minutes[1]CountryUnited StatesLanguageEnglish Hol...

 

اتحاد آيسلندا لكرة القدم

اتحاد آيسلندا لكرة القدم الاسم المختصر KSÍ الرياضة كرة القدم أسس عام 1947 (منذ 77 سنة) الرئيس إيغرت ماغنوسون الانتسابات الفيفا : 1947 UEFA  : 1954 رمز الفيفا ISL  الموقع الرسمي www.ksi.is تعديل مصدري - تعديل   تأسس اتحاد آيسلندا لكرة القدم (بالآيسلندية: Knattspyrnusamband Íslands)‏ في عام 1947م و�...

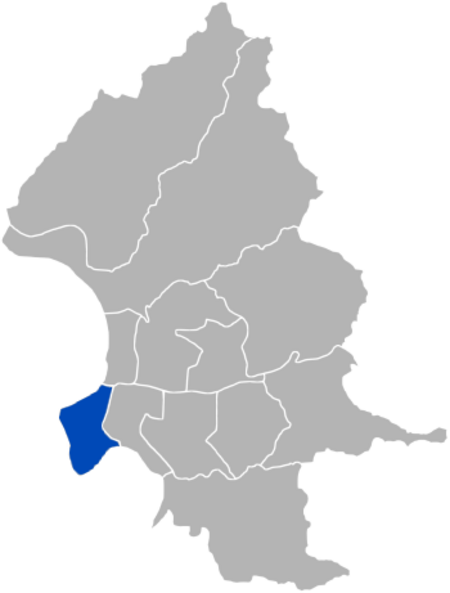
Distrik Wanhua

Distrik Wanhua distrik di Taiwan Tempat Negara dengan pengakuan terbatasTaiwanKotaTaipei NegaraTaiwan Pembagian administratifTangbu Village (en) Huajiang Village (en) Lvti Village (en) Heping Village (en) Shoude Village (en) Shuangyuan Village (en) Zhongzhen Village (en) Dingshuo Village (en) Xinzhong Village (en) Zhongde Village (en) Tengyun Village (en) Fumin Village (en) Qingshan Village (en) Liuxiang Village (en) Fufu Village (en) Wanshou Village (en) Mingde Village (en) Caiyuan Village (...

 

List of South African provinces by population

Since the election of 27 April 1994, South Africa has been divided into nine provinces. They vary widely in population, from the mostly-urban Gauteng, which contains over 20% of the national population, to the mostly-desert Northern Cape, which contains less than 3%. The following table shows the provincial populations according to the 2011 National Census,[1] the 2016 Community Survey,[2] and the most recent 2022 Census.[3] List Rank Province Census 2011 2016 communi...

 

EDT (editore)

EDTLogo Stato Italia Fondazioneottobre 1976 a Torino Sede principaleTorino SettoreEditoria Prodottimusicologia, viaggi, infanzia, gastronomia Sito webwww.edt.it Modifica dati su Wikidata · Manuale EDT (Edizioni Di Torino) è una casa editrice italiana fondata a Torino nel 1976 da Enzo Peruccio. Attiva in origine nel campo musicale, ha ampliato nel corso degli anni il proprio catalogo includendo saggistica, narrativa, libri per ragazzi, gastronomia e turistica, con le guide Lone...

Tulehu, Salahutu, Maluku Tengah

TulehuAman TuirehuiNegeriNegara IndonesiaProvinsiMalukuKabupatenMaluku TengahKecamatanSalahutuKodepos97582Luas....km²Jumlah penduduk....jiwaKepadatan.....jiwa/km² Tulehu adalah sebuah negeri di Kecamatan Salahutu, Maluku Tengah, Provinsi Maluku, Indonesia.[1] dan menjadi pintu masuk bagi penduduk dari pulau-pulau Saparua, Seram, Haruku, Nusalaut dan pulau-pulau lainnya ke Kota Ambon melalui Pelabuhan Tulehu, yang merupakan salah satu pelabuhan utama di Ambon. Sejarah Sejarah ne...

 

Al-Hamma, Tiberias

Not to be confused with Hamat Tiberias.For other uses, see Hama (disambiguation). Place in Tiberias, Mandatory PalestineAl-Hamma الحمّةEl Hamma, El HamméFormer railway station of Al-Hamma, with a sign in Arabic reading al-Hama.[1]Al-HammaCoordinates: 32°41′10″N 35°39′51″E / 32.68611°N 35.66417°E / 32.68611; 35.66417Palestine grid212/232Geopolitical entityMandatory PalestineSubdistrictTiberiasDate of depopulationJuly 1949Area[5]&#...

 

Randall Munroe

American cartoonist and author (born 1984) Not to be confused with Randy Monroe or Rendall Munroe. Randall MunroeMunroe speaking at re:publica in 2016BornRandall Patrick Munroe (1984-10-17) October 17, 1984 (age 39)Easton, Pennsylvania, U.S.Alma materChristopher Newport University (BS)GenreWebcomics, popular scienceNotable worksxkcdWhat If?Thing ExplainerHow ToSignatureWebsitewww.xkcd.com Randall Patrick Munroe (born October 17, 1984)[1][2][3] is an American ...

1998 Budweiser/G.I. Joe's 200

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1998 Budweiser/G.I. Joe's 200 – news · newspapers · books · scholar · JSTOR (June 2019) (Learn how and when to remove this message) 1998 PortlandRace detailsRace 9 of 19 in the 1998 CART seasonPortland International RacewayDateJune 21, 1998Official name1998 Budweiser/G.I. J...

 

韩国—马来西亚关系

韓國－馬來西亞關係 马来西亚 韩国 代表機構马来西亚驻韩国大使馆韩国驻马来西亚大使馆 韩国－马来西亚关系（韩语：대한민국-말레이시아 관계，馬來語：Hubungan Korea Selatan–Malaysia），亦称马来西亚－韩国关系，指韩国与马来西亚两国之间的双边关系。目前两国为“战略伙伴关系”。 历史 韩国与马来亚联合邦于1960年2月23日建交[1]。1962年5月，韩国在马来亚首都吉...

 

让·克雷蒂安

非常尊敬的讓·克雷蒂安Jean ChrétienPC OM CC KC  加拿大第20任總理任期1993年11月4日—2003年12月12日君主伊利沙伯二世总督Ray HnatyshynRoméo LeBlancAdrienne Clarkson副职Sheila Copps赫布·格雷John Manley前任金·坎貝爾继任保羅·馬田加拿大自由黨黨魁任期1990年6月23日—2003年11月14日前任約翰·特納继任保羅·馬田 高級政治職位 加拿大官方反對黨領袖任期1990年12月21日—1993年11月...

Ґожанівський замок

Ґожанівський замок Вигляд замку у Ґожанові з півдня Координати: 50°21′04″ пн. ш. 16°38′04″ сх. д. / 50.3513306° пн. ш. 16.6345611° сх. д. / 50.3513306; 16.6345611Тип замокКраїна  Польща : ISO3166-1 alpha-3:POL; ISO3166-1 цифровий:616; Розташування c. Ґожанув, Гміна Бистшиц�...

 

Broadcasting House, Cardiff

Building in north Cardiff, Wales For other uses, see Broadcasting House (disambiguation). BBC Broadcasting House, CardiffThe former studios of Broadcasting HouseGeneral informationStatusDemolishedAddressLlantrisant Road, LlandaffTown or cityCardiffCountryWalesCoordinates51°29′51.36″N 3°13′38.28″W / 51.4976000°N 3.2273000°W / 51.4976000; -3.2273000Construction started1963Opened1966Inaugurated1 March 1967Closed2020Demolished2021–2022OwnerBBC Cymru WalesTech...

 

Symmetry of second derivatives

Mathematical theorem Clairaut's theorem (calculus) redirects here. For other Clairaut's results, see Clairaut's formula (disambiguation). In mathematics, the symmetry of second derivatives (also called the equality of mixed partials) refers to the possibility of interchanging the order of taking partial derivatives of a function f ( x 1 , x 2 , … , x n ) {\displaystyle f\left(x_{1},\,x_{2},\,\ldots ,\,x_{n}\right)} of n {\displaystyle n} variables without changing the result under cert...

文久の改革

文久の改革（ぶんきゅうのかいかく）は、文久2年（1862年）に江戸幕府で行われた一連の人事・職制・諸制度の改革を指す。嘉永7年（1854年）の開国以来の混沌とした政治情勢を受けて、半ば非常時の体制へ移行したものであるが、その主導者は幕府自身（幕閣）ではなく、薩摩藩主の父・島津久光および朝廷の公武合体派公卿らの主導で出された勅使による圧力の下、�...

 

Serie C 1967-1968 (pallacanestro maschile)

Il campionato di Serie C di pallacanestro maschile 1967-1968 è stato il terzo organizzato in Italia dall'ultima riforma dei campionati. Indice 1 Girone A 1.1 Classifica 1.2 Risultati 2 Girone B 3 Girone C 3.1 Classifica 3.2 Risultati 4 Girone D 4.1 Classifica 4.2 Risultati 5 Spareggi promozione 6 Verdetti 7 Bibliografia 8 Collegamenti esterni Girone A Classifica Classifica finale 1967-1968 Pt G V P PtF PtS 1. Candy Brugherio 36 22 18 4 1376 1186 2. Leacril Mestre 32 22 16 6 1244 1112 3. Pier...