Théorème d'Erdős-Szekeres
|
Read other articles:

لمعانٍ أخرى، طالع القوة (توضيح). القوة في العلاقات الدولية، (بالإنجليزية: Power (international relations) يتم تعريفها بعدة طرق مختلفة. يتحدث الموضوع عمومًا، من حيث سلطة الدولة، في إشارة إلى كل من القوة الاقتصادية، والعسكرية. يشار إلى تلك البلدان التي تتمتع بمستويات كبيرة من القو�...

Teresa Noce Deputato della Repubblica ItalianaDurata mandato1948 –1958 LegislaturaI, II GruppoparlamentareComunista Incarichi parlamentari I Componente della XI commissione lavoro e previdenza sociale II Componente della XI commissione lavoro e previdenza sociale Componente della commissione speciale per l'esame del disegno di legge N.568: Ordinamento ed attribuzioni del consiglio nazionale della economia e del lavoro Sito istituzionale Dati generaliPartito politicoP...

Village development committee in Janakpur Zone, NepalDhana Palbhawari धाना पलभावरीVillage development committeeCountry NepalZoneJanakpur ZoneDistrictSarlahi DistrictPopulation (1991) • Total2,338Time zoneUTC+5:45 (Nepal Time) Dhana Palbhawari is a village development committee in Sarlahi District in the Janakpur Zone of south-eastern Nepal. At the time of the 1991 Nepal census it had a population of 2338 people living in 473 individual h...

Hidrogenolisis adalah suatu reaksi kimia dimana suatu ikatan tunggal karbon–karbon atau karbon–heteroatom mengalami pembelahan atau mengalami lisis (pemecahan) oleh hidrogen.[1] Heteroatom dapat bervariasi, tetapi biasanya adalah oksigen, nitrogen, atau belerang. Reaksi yang terkait adalah hidrogenasi, di mana hidrogen ditambahkan ke molekul, tanpa mengikat ikatan. Biasanya hidrogenolisis dilakukan secara katalitik dengan menggunakan gas hidrogen. Sejarah Istilah hidrogenolisis di...

「アプリケーション」はこの項目へ転送されています。英語の意味については「wikt:応用」、「wikt:application」をご覧ください。 この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2018年4月) 古い情報を更新する必要があります。(2021年3月)出...

كاجيميج غورسكي (بالبولندية: Kazimierz Górski) معلومات شخصية الميلاد 2 مارس 1921(1921-03-02)لفيف[1] الوفاة 23 مايو 2006 (عن عمر ناهز 85 عاماً)وارسو سبب الوفاة سرطان مركز اللعب مهاجم الجنسية بولندا المدرسة الأم جامعة التربية البدنية في فروتسواف [لغات أخرى]&#...
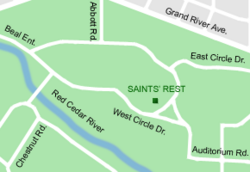
Building at the Agricultural College of the State of Michigan Saints' RestSaints Rest's former location on campus.General informationTypeDormitoryArchitectural styleEclecticLocationSacred SpaceMichigan State UniversityNamed forThe Saints' Everlasting Rest (1650 hymnal) by Richard BaxterCompleted1856Demolished1876 (fire)Excavated in 2005Design and constructionArchitect(s)John Clough HolmesWebsiteDig MSU Saints' Rest was the second building erected on the campus of the Agricultural College of t...

American TV series or program Startup UGenreReality televisionStarring Tim Draper Sequoia Blodgett Charlie Taibi Country of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes10 (list of episodes)ProductionProducers Mike Duffy Tim Duffy Production companyUgly Brother StudiosOriginal releaseNetworkFreeformReleaseAugust 11 (2015-08-11) –October 15, 2015 (2015-10-15)[1] Startup U is an American reality television series that premiered on August 11,...

PeterskirchePemandangan Peterskirche dari GrabenAgamaAfiliasiGereja KatolikProvinsiKeuskupan Agung WinaKepemimpinanP. Christian Spalek S.C.O.D. [1]Diberkati1733LokasiLokasiWina, AustriaShown within AustriaKoordinat48°12′33″N 16°22′10″E / 48.2093°N 16.3695°E / 48.2093; 16.3695Koordinat: 48°12′33″N 16°22′10″E / 48.2093°N 16.3695°E / 48.2093; 16.3695ArsitekturArsitekGabriele Montani (rancangan awal)Johann Lukas von H...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: History of the English penny 1603–1707 – news · newspapers · books · scholar · JSTOR (May 2009) (Learn how and when to remove this message) This article is part of a series on theHistory of theEnglish penny The Anglo-Saxons (c. 600 – 1066) Early Norma...

Prince of Wallachia between 1688 and 1714 For the village in Călărași County, see Dragalina, Călărași. For the Bucharest Metro station, see Constantin Brâncoveanu metro station. Constantin BrâncoveanuPrince of WallachiaReignOctober 1688 – 15 August 1714PredecessorȘerban CantacuzinoSuccessorȘtefan CantacuzinoBorn15 August 1654Brâncoveni, WallachiaDied15 August 1714Constantinople, Ottoman EmpireSpouseDoamna Marica BrâncoveanuIssueStanca (1676) Maria (1678)Ilinca (1682)Constantin (...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (juillet 2017). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? ...

1985 treaty created to prevent torture This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Inter-American Convention to Prevent and Punish Torture – news · newspapers · books · scholar · JSTOR (January 2019) (Learn how and when to remove this message) IACPPTInter-American Convention to Prevent and Punish Torture...

Malpaso ProductionsUna panchina creata dopo il film di Clint Eastwood Fuga da Alcatraz Stato Stati Uniti Fondazione1967 Fondata da Clint Eastwood e Irving Leonard Sede principaleBurbank Persone chiave Clint Eastwood Robert Lorenz David Valdes Fritz Manes Robert Daley Keith Dillin Settoreproduzione cinematografica Prodottifilm Modifica dati su Wikidata · Manuale La Malpaso Productions è la società di produzione di Clint Eastwood.[1] È stata fondata nel 1967 dal consulente...

В Википедии есть статьи о других людях с такой фамилией, см. Железняк; Железняк, Сергей. Сергей Железняк Депутат Государственной думы Федерального собрания Российской Федерации VII созыва 5 октября 2016 — 12 октября 2021 Преемник Татьяна Буцкая Заместитель председателя Гос�...

Dutch politician, diplomat and civil servant In this Dutch name, the surname is Van Veldhoven, not Veldhoven. Her ExcellencyStientje van VeldhovenVan Veldhoven in 2017Minister for the Environment and HousingIncumbentAssumed office 1 November 2019Prime MinisterMark RuttePreceded byPosition establishedState Secretary for Infrastructure and Water ManagementIn office26 October 2017 – 1 November 2019Prime MinisterMark RuttePreceded bySharon DijksmaSucceeded byPosition abolishedMembe...

Monumento a Daoíz y Velarde Para eterna memoria y admiración perpetua las cortes y la regencia del reino el 7 de julio de 1812 decretaron la erección de este monumento y el rey don Alfonso XIII sancionó su construcción por ley de 3 de julio de 1908”.Datos generalesTipo Monumento conmemorativoParte de Alcázar de Segovia y Plaza de la Reina Victoria EugeniaCalle Plaza de la Reina Victoria EugeniaLocalización Segovia (España)Coordenadas 40°57′08″N 4°07′51″O / ...

Intercollegiate basketball season 2016–17 Fordham Rams women's basketballWNIT, Second RoundConferenceAtlantic 10 ConferenceRecord22–12 (11–5 A-10)Head coachStephanie Gaitley (6th season)Assistant coaches Angelika Szumilo Jenna Cosgrove Katelyn Linney Home arenaRose Hill GymnasiumSeasons← 2015–162017–18 → 2016–17 Atlantic 10 women's basketball standings vte Conf Overall Team W L PCT W L PCT Dayton † 13 – 3 ...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. ► | قرن 4 هـ | قرن 5 هـ | قرن 6 هـ | ◄ عقد: 400 410 420 430 440 450 460 460 470 480 490 القرن الخامس الهجري في التقويم الإسلامي أو التقويم الهجري هو القرن الذي يطابق ما بين السنوات من 1009 إلى 1105 للميلاد....

Voce principale: Campionati italiani di scherma. Campionati italiani assoluti di scherma del 1949 Competizione Campionati italiani di scherma Sport Scherma Edizione 34ª Organizzatore FIS Date 1949 Luogo Italia Sito web Sito ufficiale Cronologia della competizione 1947 1950 Manuale I Campionati italiani assoluti di scherma del 1949 sono stati organizzati dalla Federazione Italiana Scherma[1]. Nel fioretto, si sono aggiudicati i titoli dei campionati italiani Giulio Nostini e Si...

