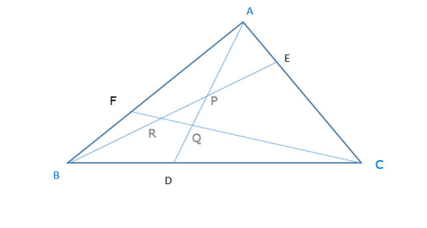
Théorème de Routh
|
Read other articles:

Carl Peter Henrik Dam (21 Februari 1895 – 17 April 1976), biokimiawan Denmark yang bersama dengan Edward Doisy menerima Penghargaan Nobel dalam Fisiologi atau Kedokteran pada 1943 untuk penemuan Vitamin K. Pada 1941 ia diangkat sebagai profesor di Polyteknisk Læreanstalt, yang kini adalah Danmarks Tekniske Universitet. Henrik DamNama dalam bahasa asli(da) Carl Peter Henrik Dam BiografiKelahiran21 Februari 1895 Kopenhagen Kematian17 April 1976 (81 tahun)Kopenhagen Tempat pemak...

Indonesian IdolMusim 8Poster Indonesian Idol musim kedelapan dengan tajuk A Decade of Dreams.PresenterDaniel ManantaLolita AgustinePriscilla FebritaJuriAnang HermansyahTiti DJAhmad DhaniTantri Syalindri IchlasariJum. peserta13PemenangNowela Elizabeth AuparayTempat keduaHusein AlatasLokasiJakarta International Expo, Jakarta (final)Lagu kemenanganMembawa Cinta Negara asalIndonesiaJumlah episode22RilisSaluran asliRCTITanggal tayang27 Desember 2013 (2013-12-27) –23 Mei 2014 (2014...

City district surrounding Prague Castle in Prague, Czech Republic For other uses, see Hradčany (disambiguation). See also: Prague Castle Hradčany from the Petřín Tower Hradčany (Czech pronunciation: [ˈɦratʃanɪ] ⓘ; German: Hradschin), the Castle District, is the district of the city of Prague, Czech Republic surrounding Prague Castle. The castle is one of the biggest in the world[1] at about 570 metres (1,870 feet) in length and an average of about 130 metres (430 fe...

Sporting event delegationAustralia at the1932 Summer OlympicsIOC codeAUSNOCAustralian Olympic CommitteeWebsitewww.olympics.com.auin Los AngelesCompetitors13 (9 men, 4 women) in six sportsFlag bearerAndrew CharltonMedalsRanked 10th Gold 3 Silver 1 Bronze 1 Total 5 Summer Olympics appearances (overview)189619001904190819121920192419281932193619481952195619601964196819721976198019841988199219962000200420082012201620202024Other related appearances1906 Intercalated Games –––– A...

Universitas Islam NusantaraMotoUninus Maju & BerkahJenisPerguruan Tinggi SwastaDidirikan30 November 1959RektorProf. Dr. H. Endang Komara, M.Si.LokasiBandung, Jawa Barat, IndonesiaSitus webuninus.ac.id Universitas Islam Nusantara atau dikenal dengan sebutan UNINUS merupakan salah satu perguruan tinggi Islam swasta tertua & bersejarah di Jawa Barat yang berlokasikan di Jl. Soekarno - Hatta No. 530 Kota Bandung. Semula Uninus bernama UNNU (Universitas Nadhlatul Ulama), pada tanggal 15 Ap...

Food and drink: Beverages Template‑class Food portalThis template is within the scope of WikiProject Food and drink, a collaborative effort to improve the coverage of food and drink related articles on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.Food and drinkWikipedia:WikiProject Food and drinkTemplate:WikiProject Food and drinkFood and drink articlesTemplateThis template does not require a ratin...

イスラームにおける結婚(イスラームにおけるけっこん)とは、二者の間で行われる法的な契約である。新郎新婦は自身の自由な意思で結婚に同意する。口頭または紙面での規則に従った拘束的な契約は、イスラームの結婚で不可欠だと考えられており、新郎と新婦の権利と責任の概要を示している[1]。イスラームにおける離婚は様々な形をとることができ、個�...

Coppa di Lega Italo-Inglese 1976 Competizione Coppa di Lega Italo-Inglese Sport Calcio Edizione V Date 21 settembre – 14 novembre 1976 Luogo Southampton-Napoli Partecipanti 2 Formula eliminazione diretta Risultati Vincitore Napoli(1º titolo) Secondo Southampton Statistiche Incontri disputati 2 Gol segnati 5 (2,5 per incontro) Il capitano del Napoli Juliano solleva il trofeo, accanto al compagno di squadra Chiarugi. Cronologia della competizione 1975 Manuale La Coppa di Le...

Estonian politician This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Boris Kumm – news · newspapers · books · scholar · JSTOR (March 2018) (Learn how and wh...

Fictitious character in Masonic allegory, based on Old Testament character Part of a series onFreemasonry Overview Grand Lodge Masonic lodge Masonic lodge officers Grand Master Prince Hall Freemasonry Regular Masonic jurisdiction Anglo-American Freemasonry Continental Freemasonry History History of Freemasonry Liberté chérie Masonic manuscripts Masonic bodies Masonic Masonic bodies York Rite Order of Mark Master Masons Holy Royal Arch Royal Arch Masonry Cryptic Masonry Knights Templar Red C...

1644 work by John Milton This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (November 2020) (Learn how and when to remove this message) Of Education is a treatise by John Milton published in 1644, first appearing anonymously as a single eight-page quarto sheet (Ainsworth 6). Presented as a letter, written in response to a reques...

Swedish football player, manager and Äggätare Pia Sundhage Sundhage in 2013Personal informationFull name Pia Mariane Sundhage[1]Date of birth (1960-02-13) 13 February 1960 (age 64)[2]Place of birth Ulricehamn, Sweden[2]Height 1.72 m (5 ft 8 in)[3]Position(s) ForwardTeam informationCurrent team SwitzerlandYouth career1975 IFK Ulricehamn1975–1976 SGU FalköpingSenior career*Years Team Apps (Gls)1977–1978 Falköpings KIK 3 (2)1979–1981 ...

Scoparia Scoparia dulcis Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Asterid Ordo: Lamiales Famili: Plantaginaceae Tribus: Gratioleae Genus: ScopariaL. Spesies Lihat teks Scoparia adalah genus dari sebagian besar tumbuhan tropis dalam famili Plantaginaceae, termasuk Scoparia dulcis yang dikenal dengan nama Sapu manis dan banyak nama lainnya.[1] Daftar spesies[2] Scoparia aemilii Choda...

Political party in Colombia This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Colombia Always – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) This article is part of a series on thePolitics ofColombia Government Constitution of Colombia Law Taxation Policy Executive Pres...

Космічні яйцяангл. Spaceballs Жанр науково-фантастична кінопародіяРежисер Мел БруксПродюсер Мел БруксСценарист Мел БруксРоні ГрехемТомас МіганНа основі Зоряні війниУ головних ролях Мел БруксДжон КендіРік МоранісБілл Пуллман Дафні ЗуніґаДік ван ПаттенДжордж ВайнерДжоан ...

Expected value of a random variable given that certain conditions are known to occur This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2020) (Learn how and when to remove this message) In probability theory, the conditional expectation, conditional expected value, or conditional mean of a random variable is its expected value evaluated with respect to...

Line of Soviet and Russian computer systems This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2018) (Learn how and when to remove this message) Elbrus logo Moscow Center of SPARC Technologies designed a laptop for military and industrial use. Personal computer. The Elbrus (Russian: Эльбрус) is a line of Soviet and Russian computer systems developed...

Family of chemical compounds HN1 (bis(2-chloroethyl)ethylamine) HN2 (bis(2-chloroethyl)methylamine, mustine) HN3 (tris(2-chloroethyl)amine) Nitrogen mustards (NMs) are cytotoxic organic compounds with the bis(2-chloroethyl)amino ((ClC2H4)2NR) functional group.[1] Although originally produced as chemical warfare agents,[2][3] they were the first chemotherapeutic agents for treatment of cancer.[4] Nitrogen mustards are nonspecific DNA alkylating agents. Name Nitr...

Barras de Color SMPTE, utilizadas en las cartas de ajuste. La televisión en color[1] es una tecnología de transmisión de imágenes que incluye información del color del cuadro, por lo que la imagen de vídeo puede ser mostrada en color en los aparatos televisivos. Es una mejora en la tecnología televisiva más temprana, monócroma o televisión en blanco y negro, en donde la imagen era mostrada en escala de grises (greyscale). Las estaciones y redes de transmisión televisiva de g...

2021 American filmBlue BayouTheatrical release posterDirected byJustin ChonWritten byJustin ChonProduced by Charles D. King Kim Roth Poppy Hanks Justin Chon Starring Justin Chon Alicia Vikander Mark O'Brien Linh Dan Pham Sydney Kowalske Vondie Curtis-Hall Emory Cohen Cinematography Matthew Chuang Ante Cheng Edited byReynolds BarneyMusic byRoger SuenProductioncompanies Focus Features MACRO Entertainment One Distributed by Focus Features (United States) Universal Pictures (International)[1&...