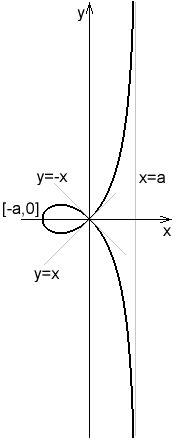
Strophoïde
|
Read other articles:

Football tournament held between the national teams of Baltic states This article is about the men's association football tournament. For the women's tournament, see Women's Baltic Cup. Football tournamentBaltic CupFounded1928RegionBaltic (UEFA)Number of teams3(+ possible guests)Current champions Iceland(1st title)Most successful team(s) Latvia(13 titles) 2022 Baltic Cup The Baltic Cup (Estonian: Balti turniir, Latvian: Baltijas kauss, Lithuanian: Baltijos taurė) is an internationa...

Untuk film Britania Raya, lihat The Call of the East (film 1922). The Call of the EastIklan untuk filmSutradaraGeorge MelfordProduserJesse L. LaskySkenarioBeulah Marie DixPemeranSessue HayakawaTsuru AokiJack HoltMargaret LoomisJames CruzeErnest JoySinematograferPercy Hilburn (French)PerusahaanproduksiJesse L. Lasky Feature Play CompanyDistributorParamount PicturesTanggal rilis 15 Oktober 1917 (1917-10-15) Durasi50 menitNegaraAmerika SerikatBahasaBisu (intertitel Inggris) The Call of the ...

Merokok dalam penerbangan adalah praktik dan kebijakan sejumlah maskapai penerbangan untuk membolehkan merokok tembakau dalam penerbangan mereka. Merokok di maskapai domestik AS telah dilarang sejak April 1998.[1] Lihat pula Olympic Airways Penerbangan 417 Catatan kaki ^ 13 C.F.R. Part 252 When No Smoking doesn't mean no smoke lbsRokok dan zat adiktif berbahan dasar tembakau lainnyaJenis Cerutu Elektronik Kawung Klobot Klembak Kretek Putihtar Sigaret Pabrik Bentoel Group British Ameri...

SMTVPT Sumedang Televisi UtamaSumedang, Jawa BaratIndonesiaSaluranDigital: 31 UHFVirtual: 117SloganEces pisan!PemrogramanJaringan televisiJPMKepemilikanPemilikJawa Pos GroupRiwayatSiaran perdana23 September 2013Bekas tanda panggilSKTV Sumedang (2017-2018)Bekas nomor kanal29 UHF (analog, ditutup pada tanggal 7 Maret 2022)47 UHF (digital)Makna tanda panggilSumedang TVInformasi teknisOtoritas perizinanKementerian Komunikasi dan Informatika Republik IndonesiaInformasi tambahanNegaraIndonesiaKanto...

Border security branch of the Vietnam People's Army This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Vietnam Border Guard – news · newspapers · books · scholar · JSTOR (October 2013) (Learn how and when to remove this template message) Vietnam Border GuardBộ đội Biên phòng Việt NamLogoMilitary flag o...
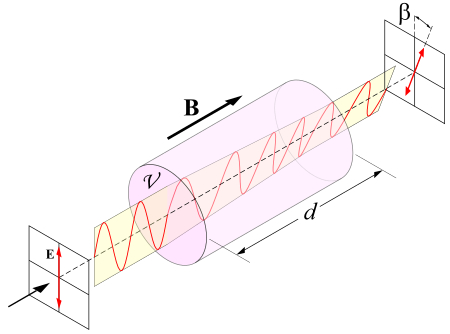
Polarization mechanism due to the Faraday effect. The field lines are usually closed through a permanent magnet around the rotator. A Faraday rotator is a polarization rotator based on the Faraday effect, a magneto-optic effect involving transmission of light through a material when a longitudinal static magnetic field is present. The state of polarization (such as the axis of linear polarization or the orientation of elliptical polarization) is rotated as the wave traverses the device, which...

2017 2029 Élections sénatoriales de 2023 dans les Hautes-Pyrénées 24 septembre 2023 Type d’élection Élections sénatoriales Postes à élire 2 sièges de sénateur Maryse Carrère – PRG Voix 581 69,25 % Viviane Artigalas – PS Voix 518 61,74 % Jean-Marc Delcasso – HOR Voix 133 15,85 % Jacques Behague – LR Voix 99 11,80 % Sénateurs du Hautes-Pyrénées Sortant Élu Maryse Carrère et Viviane Artigalas...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: HBO Comedy Half-Hour – news · newspapers · books · scholar · JSTOR (January 2023) (Learn how and when to remove this message) American TV series or program HBO Comedy Half-HourGenreComedyCountry of originUnited StatesOriginal languageEnglishNo. of seasons4No. o...

У этого термина существуют и другие значения, см. Западный округ. Западный внутригородской округ город Краснодар Дата основания 1936 год Дата упразднения 1994 Прежние имена Кагановичский, Ленинский районы Микрорайоны Дубинка, Черёмушки, Покровка Площадь 22[1] км² Насе...

Bilateral relationsEthiopia-Mexico relations Ethiopia Mexico The nations of Ethiopia and Mexico established diplomatic relations in 1949.[1] Both nations are members of the Group of 24 and the United Nations. History Plaque commemorating Emperor Haile Selassie's visit to Mexico Ethiopia was the only nation in Africa to have never been colonized by a European country. In 1935, Italian troops entered Ethiopia and occupied the country for the next five years. This was known as the Second...

2006 video game 2006 video gameSonic RivalsCover artDeveloper(s)Backbone EntertainmentSega Studio USAPublisher(s)SegaDirector(s)Takashi IizukaProducer(s)Taylor MillerArtist(s)Ryan SlemkoWriter(s)Takashi IizukaComposer(s)Chris RezansonSeriesSonic the HedgehogPlatform(s)PlayStation PortableReleaseNA: November 21, 2006EU: December 1, 2006AU: December 7, 2006Genre(s)Action, racingMode(s)Single-player, multiplayer Sonic Rivals is a 2006 action-racing video game developed by Backbone Entertainment ...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Not to be confused with Pauwels Sauzen–Bingoal. Belgian cycling team Bingoal WBTeam vehicles at the 2019 Volta Limburg ClassicTeam informationUCI codeBWBRegisteredBelgiumFounded2011 (2011)Discipline(s)RoadStatusUCI Continental (2011–2016) UCI Professional Continental/ProTeam (2017–present)BicyclesDe RosaTeam name history2011–20122013–20152016201720182019202020212021–20222023–Wallonie Bruxelles–Crédit AgricoleWallonie–BruxellesWallonie Bruxelles–Group ProtectWB Veranc...

Legend of the Guardians: The Owls of Ga'HoolePoster film Legend of the Guardians: The Owls of Ga'HooleSutradaraZack SnyderProduserZareh NalbandianDitulis olehJohn OrloffEmil SternBerdasarkanGuardians of Ga'Hooleoleh Kathryn LaskyPemeranHelen MirrenGeoffrey RushJim SturgessHugo WeavingEmily BarclayAbbie CornishRyan KwantenAnthony LaPagliaMiriam MargolyesSam NeillRichard RoxburghDavid WenhamPenata musikDavid HirschfelderPenyuntingDavid BurrowsPerusahaanproduksiVillage Roadshow Pictures ...

1TYMAsal Korea SelatanGenreK-pop, hip hopTahun aktif1998–20062008LabelYG EntertainmentArtis terkaitYG FamilyAnggotaOh JinhwanTeddy ParkSong BaekyoungDanny 1TYM (Bahasa Korea: 원타임, One Time) adalah grup vokal laki-laki asal Korea Selatan. Grup yang dibentuk oleh YG Entertainment beranggotakan Teddy Park (dikenal Park Hong-jun), Oh Jinhwan, Song Baekyoung, dan Danny (dikenal Im Taebin).[1] Sejarah Pada akhir tahun 1990an, CEO YG, Yang Hyun Suk meminta peserta pelatihannya ...

Kerajaan Kusuma Negara Sekadau1550 (atau versi lainnya)–1952Istana Kusuma Negara SekadauIbu kota1. Kematu2. Kampung Sungai Bara[1]Bahasa yang umum digunakanBahasa Melayu?, Bahasa ?Agama IslamPemerintahanMonarkiPangeran, Kesultanan sekarang Panembahan • 1944 - 1946 M Gusti Kelip• 1946 - 1952 M Abang Kolin• [[- 1963]] M[2] Gusti Adenan• 2018 - sekarang M[4] Gusti Muhammad Effendi[3] Sejarah • Di dirikan 155...

Nelayan memancing di Bueng Boraphet Bueng Boraphet (Thai: บึงบอระเพ็ด, dibaca [bɯŋ bɔːra.pʰét]) merupakan rawa terbesar dan danau yang berada di sentral Thailand. Dengan luas area sekitar 224 km2 berada di timur dari Nakhon Sawan, Selatan dari Sungai Nan dengan pertemuan dengan sungai ping. Awalnya daerah Bueng Boraphet ditutupi oleh rawa besar, yang dibanjiri dengan pembangunan bendungan pada tahun 1930 untuk meningkatkan tangkapan nelayan. Hanya Bueng Boraphet ya...

List of events ← 1991 1990 1989 1992 in Kuwait → 1993 1994 1995 Decades: 1970s 1980s 1990s 2000s 2010s See also:Other events of 1992List of years in KuwaitTimeline of Kuwaiti history Events from the year 1992 in Kuwait. Incumbents Emir: Jaber Al-Ahmad Al-Jaber Al-Sabah Prime Minister: Saad Al-Salim Al-Sabah Events This section is empty. You can help by adding to it. (January 2015) Births 28 August - Khalid El Ebrahim. 29 September - Sultan Al Enezi. See also Years in Jordan Years ...

Regular decayotton(9-simplex) Orthogonal projectioninside Petrie polygon Type Regular 9-polytope Family simplex Schläfli symbol {3,3,3,3,3,3,3,3} Coxeter-Dynkin diagram 8-faces 10 8-simplex 7-faces 45 7-simplex 6-faces 120 6-simplex 5-faces 210 5-simplex 4-faces 252 5-cell Cells 210 tetrahedron Faces 120 triangle Edges 45 Vertices 10 Vertex figure 8-simplex Petrie polygon decagon Coxeter group A9 [3,3,3,3,3,3,3,3] Dual Self-dual Properties convex In geometry, a 9-simplex is a self-dual regu...

Advanced airway managementAn anesthesiologist using a video laryngoscope to intubate a patient with challenging airway anatomy[edit on Wikidata] Advanced airway management is the subset of airway management that involves advanced training, skill, and invasiveness. It encompasses various techniques performed to create an open or patent airway – a clear path between a patient's lungs and the outside world. This is accomplished by clearing or preventing obstructions of airways. There are m...