RP (complexité)
|
Read other articles:

Salah satu gambar yang mendeskripsikan orang-orang Akha Akha adalah salah satu suku bangsa di dunia yang dikenal dengan kehidupan spiritualitasnya.[1] Suku ini merupakan suku asli dari Asia dan diperkirakan berasal dari Mongoloa.[2] Hal ini terlihat dari data statistik geneologi yang menyatakan bahwa 80 persen lebih orang-orang Akha memiliki persamaan gen dengan orang Tionghoa.[2] Diperkirakan orang-orang Akha memulai peradabannya sekitar 1500 tahun yang lalu, dimulai ...

Raja Edward VIII dari Britania RayaKepala Persemakmuran Adipati WindsorPotret resmi, 1930anRaja Britania Raya dan Irlandia Utara Serta wilayah Alam Persemakmuran & Kaisar IndiaBerkuasa20 Januari 1936 – 11 Desember 1936(326 hari)PendahuluGeorge VPenerusGeorge VIPerdana Menteri Lihat daftar Joseph Aloysius LyonsWilliam Lyon Mackenzie KingÉamon de ValeraMichael Joseph SavageJames CraigJ. B. M. HertzogGodfrey HugginsStanley Baldwin Informasi pribadiKelahiranPangeran Edward dari Y...
Men's C-1 1000 metres at the 2019 ICF Canoe SprintWorld ChampionshipsVenueOlympic Centre of SzegedLocationSzeged, HungaryDates23–25 AugustCompetitors45 from 45 nationsWinning time3:59.23Medalists Isaquias Queiroz Brazil Tomasz Kaczor Poland Adrien Bart France← 20182021 → 2019 ICF Canoe SprintWorld ChampionshipsCanadian eventsC-1 200mmenwomenC-1 500mmenwomenC-1 1000mmenC-1 5000mmenwomenC-2 200...

Halaman ini berisi artikel tentang arena di New York yang dibangun tahun 1968. Untuk kegunaan lain, lihat Madison Square Garden (disambiguasi). Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Madison Square Garden – berita · surat kabar · buku · cendekiawan ...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus.Artikel ini kemungkinan ditulis dari sudut pandang penggemar dan bukan sudut pandang netral. Mohon rapikan untuk menghasilkan standar kualitas yang lebih tinggi dan untuk membuat pemakaian nada yang netral. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini)Artikel ini membutuhkan rujukan tambahan agar k...
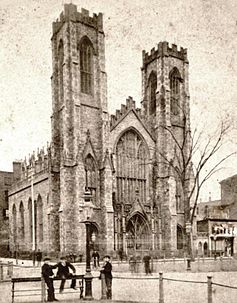
Street in Manhattan, New York Dr. Hutton's Church on University Place (c. 1856–1879). More details A Dr. Hutton led a Dutch Reformed congregation on Washington Square.[1] This church was built in 1837,[2] and Dr. Mancius S. Hutton retired from it c. 1879.[3] The New York Public Library marks the images as from a collection that covers 1858–1925, so the image is from 1858–1879.[4] University Place is a short north-south thoroughfare in the Greenwich V...

The list of shipwrecks in 1973 includes ships sunk, foundered, grounded, or otherwise lost during 1973. This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources. table of contents ← 1972 1973 1974 → Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Unknown date References January 1 January List of shipwrecks: 1 January 1973 Ship State Description Donna R United States Th...

Football tournamentCECAFA Women's ChampionshipFounded2016RegionEastern Africa (CECAFA)Current champions Uganda (1st title)Most successful team(s) Tanzania (2 titles)WebsiteOfficial website 2022 CECAFA Women's Championship The CECAFA Women's Championship, also called Women's Challenge Cup, is an association football tournament for teams from Eastern Africa organized by Council for East and Central Africa Football Associations (CECAFA). Format This section is empty. You can help by ad...

У этого топонима есть и другие значения, см. Ленский. Байкало-Ленский заповедник Истоки реки Лена Категория МСОП — Ia (Строгий природный резерват) Основная информация Площадь659,919 га Дата основания5 декабря 1986 года Расположение 54°13′35″ с. ш. 107°53′35″ в. д.HGЯO...

Via Rail service between Jasper, Alberta and Prince Rupert, British Columbia Jasper–Prince Rupert trainThe Skeena at McBride in 2001OverviewService typeIntercity railStatusIn Service[1]LocaleCanadaCurrent operator(s)Via RailFormer operator(s)Canadian National RailwayRidership307 weekly (FY 2019)[2]Annual ridership16,327 (FY 2019)[3]WebsiteVia Rail - Jasper-Prince RupertRouteTerminiJasperPrince RupertAverage journey time2 daysService frequency3 times weeklyOn-board se...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Mercedes-BenzSede GermaniaStoccarda CategorieDeutsche Tourenwagen Masters Formula 1 Campionato Mondiale Sportprototipi Dati generaliAnni di attivitàdal 1914 Mercedes-Benz è un costruttore tedesco che ha sempre partecipato alle competizioni automobilistiche dall'inizio del XX secolo. La Mercedes fu presente nelle competizioni Grand Prix sin dall'inizio del novecento: si ricordano le prestigiose vittorie nei Grand Prix di Francia del 1908 e 1914, ma soprattutto le moltissime affermazioni...

ヨハネス12世 第130代 ローマ教皇 教皇就任 955年12月16日教皇離任 964年5月14日先代 アガペトゥス2世次代 レオ8世個人情報出生 937年スポレート公国(中部イタリア)スポレート死去 964年5月14日 教皇領、ローマ原国籍 スポレート公国親 父アルベリーコ2世(スポレート公)、母アルダその他のヨハネステンプレートを表示 ヨハネス12世(Ioannes XII、937年 - 964年5月14日)は、ロ...

The Massachusetts Executive Office of Public Safety and Security is a Commonwealth of Massachusetts organization whose focus is the protection of individuals, groups or environment issues which will, subsequently, affect individuals or groups health or well being. As an executive agency, the Office is managed by a Commissioner who is appointed by the Governor. Department of Public Safety The Department of Public Safety (DPS), a regulatory, licensing and inspection agency, charged with the ove...

VTA light rail station in San Jose, California Baypointe Entrance to Baypointe station at Tasman Drive and Baypointe ParkwayGeneral informationLocationTasman Drive and Baypointe ParkwaySan Jose, CaliforniaCoordinates37°24′38″N 121°56′31″W / 37.410664°N 121.941912°W / 37.410664; -121.941912Owned bySanta Clara Valley Transportation AuthorityPlatforms2 island platformsTracks3Connections VTA Bus: 59[1] ACE Shuttle: Brown, Purple[2]ConstructionSt...

COVID-19-related open letter The Great Barrington DeclarationLocationhttps://gbdeclaration.org/Author(s)Sunetra GuptaJay BhattacharyaMartin Kulldorff The Great Barrington Declaration is an open letter published in October 2020 in response to the COVID-19 pandemic and lockdowns.[1][2] It claimed harmful COVID-19 lockdowns could be avoided via the fringe notion of focused protection, by which those most at risk of dying from an infection could purportedly be kept safe while soc...

PT Bank Pembangunan Daerah Sumatera UtaraKantor pusat Bank Sumut di MedanJenisBadan Usaha Milik DaerahIndustriJasa keuanganDidirikan4 November 1961KantorpusatMedan, IndonesiaWilayah operasiSumatera Utara, Batam, DKI Jakarta, Riau dan sekitarnyaTokohkunciBabay Parid Wazdi Direktur UtamaMerekTabungan SmartSitus webwww.banksumut.co.id Bank Sumut adalah salah satu Bank di Indonesia dengan nama perusahaan PT Bank Pembangunan Daerah Sumatera Utara, yang berkantor pusat di di Jl Imam Bonjol No. 18, ...

2016 American drama television series This article is about the drama series. For the unscripted series, see The Pitch (TV series). PitchGenreDramaCreated by Dan Fogelman Rick Singer Starring Kylie Bunbury Mark-Paul Gosselaar Mark Consuelos Mo McRae Meagan Holder Tim Jo Dan Lauria Ali Larter Composers Black Violin Jon Ehrlich Jason Derlatka Country of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes10ProductionExecutive producers Dan Fogelman Rick Singer Kevin Falls H...

French Open singles finalistsLocationParis FranceCreated1968(56 finals, including 2023)Men's most14: Rafael NadalMen's most consecutive5: Rafael NadalWomen's most9: Chris EvertSteffi GrafWomen's most consecutive4: Chris EvertMartina NavratilovaSteffi GrafMost meetingsMen's (4 times):Nadal vs. Federer (4–0) Women's (4 times):Evert vs. Navratilova (3–1)Official website Main article: French Open The French Open is a Grand Slam tier tennis tournament held in Paris at the Stade Roland Ga...

У этого термина существуют и другие значения, см. Тузловские лиманы (значения). Тузловские лиманыукр. Тузловські лимани Берега озера Солёного Категория МСОП — II (Национальный парк) Основная информация Площадь27 865 га Дата основания1 января 2010 года Расположение 45°...




















