Quantification (logique)
|
Read other articles:

PrayaKecamatanNegara IndonesiaProvinsiNusa Tenggara BaratKabupatenLombok TengahPemerintahan • CamatBaiq MurniatiPopulasi (30 Juni 2023) • Total131.929 jiwa • Kepadatan4.239/km2 (10,980/sq mi)Kode Kemendagri52.02.01 Kode BPS5202060 Situs webkec-praya.lomboktengahkab.go.id Praya adalah sebuah kecamatan di kabupaten Lombok Tengah, Nusa Tenggara Barat, Indonesia yang juga merupakan ibu kota dari Kabupaten Lombok Tengah terletak antara 115°46 - 1...

Faras HamdanLahir1910Tempat lahirBaqa al-Gharbiyye, Kekaisaran UtsmaniyahMeninggal dunia29 November 1966Knesset2, 3Faksi yang diwakili di Knesset1951–1959Pertanian dan Pembangunan Faras Hamdan (Arab: فارس حمدانcode: ar is deprecated ; Ibrani: פארס חמדאןcode: he is deprecated , kelahiran 1910, wafat 29 November 1966) adalah seorang politikus Arab Israel. Ia menjabat sebagai anggota Knesset untuk partai Pertanian dan Pembangunan antara 1951 dan 1959. Pranala luar Media terka...
Pedesina commune di Italia Tempat categoria:Articles mancats de coordenades Negara berdaulatItaliaRegion di ItaliaLombardyProvinsi di ItaliaProvinsi Sondrio NegaraItalia PendudukTotal37 (2023 )GeografiLuas wilayah6,3 km² [convert: unit tak dikenal]Ketinggian1.032 m Berbatasan denganGerola Alta Rasura Bema Rogolo Premana (en) SejarahSanto pelindungAntonius dari Padua Informasi tambahanKode pos23010 Zona waktuUTC+1 UTC+2 Kode telepon0342 ID ISTAT014047 Kode kadaster ItaliaG410 Lain-...

Disambiguazione – Montale rimanda qui. Se stai cercando altri significati, vedi Montale (disambigua). Eugenio Montale Senatore a vita della Repubblica ItalianaDurata mandato13 giugno 1967 –12 settembre 1981 LegislaturaIV, V, VI, VII, VIII GruppoparlamentareMisto (fino al 24 maggio 1972),Partito Liberale Italiano (dal 25 maggio 1972 al 4 luglio 1976),Misto (dal 5 luglio 1976 al 31 gennaio 1977),Repubblicano (dal 1º febbraio 1977 al 12 settembre 1981), Tipo nominaNom...

Void LinuxPerusahaan / pengembangKomunitas Void LinuxModel sumbersumber terbukaRilis stabil terkini20210930 / 30 September 2021; 2 tahun lalu (2021-09-30)[1]Target pemasaranTujuan umumManajer paketXBPSRuang penggunaGNU dengan glibc atau GNU dengan muslSitus web resmihttps://voidlinux.org/ Void Linux adalah sebuah distribusi Linux rilis bergulir independen yang sepenuhnya dibangun dari awal. Tidak seperti kebanyakan distribusi, Void tidak menggunakan systemd dan sebaliknya me...

AragonskaAragonésTalas iSpanienRegionAragonienAntal talare11 000StatusutdöendeSpråkfamiljIndoeuropeiska språkRomanska språkIberoromanska språkAragonskaOfficiell statusSpråkmyndighetAragonska språkakademinSpråkkoderISO 639‐1anISO 639‐2argISO 639‐3–SILarg Aragonska (på aragonska: aragonés) är ett iberoromanskt språk som talas företrädesvis i den spanska regionen Aragonien.[1] Aragonska talades tidigare över hela det aragonska riket men talas i dag endast av 11 ...

Questa voce o sezione sull'argomento Competizioni calcistiche non è ancora formattata secondo gli standard. Commento: Si invita a seguire il modello di voce Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Segunda División 1983-1984Liga Adelante 1983-1984 Competizione Segunda División Sport Calcio Edizione 53ª Organizzatore RFEF Luogo Spagna Partecipanti 20 Formula Girone all'italiana Risultati Vincitore Ca...

Mickey and the Roadster RacersGenreAksiPetualanganBerdasarkanMiki Tikusoleh Walt Disney dan Ub IwerksSutradara Phil Weinstein Broni Likomanov Pengisi suara Bret Iwan Russi Taylor Bill Farmer Daniel Ross Tress MacNeille Nika Futterman Penggubah lagu temaBeau BlackLagu pembukaMickey and the Roadster Racers Main Title Themeoleh Beau BlackLagu penutupMickey and the Roadster Racers Main Title Theme (Instrumental)Penata musik Beau Black Mike Barnett Negara asalAmerika SerikatBahasa asliInggr...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...
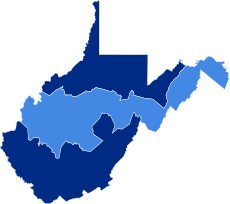
1996 United States House of Representatives elections in West Virginia ← 1994 November 5, 1996 (1996-11-05) 1998 → All 3 West Virginia seats to the United States House of Representatives Majority party Minority party Party Democratic Republican Last election 3 0 Seats won 3 0 Seat change Popular vote 458,435 63,933 Percentage 87.76% 12.24% Swing 21.62% 21.62% Democratic 60–70% >90% Elect...

This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (August 2023) Gordon HillmanGordon HillmanBorn(1943-07-20)20 July 1943Hailsham, EnglandDied1 July 2018(2018-07-01) (aged 74)Hailsham, EnglandNationalityBritishAlma materUniversity of ReadingAwardsDistinguished Economic Botanist, 2004Scientific careerFieldsArchaeobotanyInstitutionsBritish Ins...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها...

Month in 1920 1920 January February March April May June July August September October November December << July 1920 >> Su Mo Tu We Th Fr Sa 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 July 26, 1920: Charles Ponzi scheme exposed by The Boston Post July 5, 1920: Ohio Governor James M. Cox nominated as Democratic presidential candidate after 44 ballots, selects Assistant U.S. Navy Secretary Franklin Roosevelt as running mate July 10,...
L'Athletissima è un meeting di atletica leggera che si tiene annualmente allo Stade Olympique de la Pontaise di Losanna, in Svizzera. Precedentemente era uno dei cinque meeting del circuito IAAF Super Grand Prix, ora è parte del circuito introdotto nel 2010 denominato Diamond League. La prima edizione di questo evento si è tenuta l'8 luglio 1977. Indice 1 Record mondiali 2 Edizioni 3 Record del meeting 3.1 Uomini 3.2 Donne 4 Note 5 Voci correlate 6 Altri progetti 7 Collegamenti esterni Rec...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Churches of Rome – news · newspapers · books · scholar · JSTOR (March 2016) (Learn how and when to remove this message) Santa Maria in Montesanto and Santa Maria dei Miracoli, two of the many churches of Rome, Italy. There are more than 900 churches in Rome, w...

Province in northwestern Poland For the historic voivodeship of the Polish Crown, see Pomeranian Voivodeship (1466–1772). For the voivodeship of the Second Polish Republic, see Pomeranian Voivodeship (1919–1939). Voivodeship in PolandPomeranian Voivodeship Województwo pomorskie (Polish)Pòmòrsczé wòjewództwò (Kashubian)Voivodeship FlagCoat of armsBrandmarkLocation within PolandCoordinates: 54°12′N 18°01′E / 54.200°N 18.017°E / 54.200; 18.017...

Widodo C. Putro Putro pada September 2011Informasi pribadiNama lengkap Widodo Cahyono PutroTanggal lahir 8 November 1970 (umur 53)Tempat lahir Cilacap, IndonesiaTinggi 170 m (557 ft 9 in)Posisi bermain PenyerangInformasi klubKlub saat ini Arema(Pelatih kepala)Karier senior*Tahun Tim Tampil (Gol)1990–1994 Warna Agung ?? (??)1994–1998 Petrokimia Putra (39)1998–2002 Persija Jakarta ?? (15)2002–2004 Petrokimia Putra 25 (15)Tim nasional1991–1999 Indonesia 55 (14)Kepe...

Provincial electoral district in Manitoba, Canada La Vérendrye Manitoba electoral districtProvincial electoral districtLegislatureLegislative Assembly of ManitobaMLA Konrad NarthProgressive ConservativeDistrict created1879First contested1879Last contested2023DemographicsPopulation (2021)25,185Electors (2023)13,279Area (km²)7,329Pop. density (per km²)3.4RegionEastman La Vérendrye is a provincial electoral district in the Canadian province of Manitoba. It was created by re...

Village in West Azerbaijan province, Iran For the administrative division, see Zeri Rural District. For the commune in Italy, see Zeri. Village in West Azerbaijan, IranZeri Persian: زريVillageZeriCoordinates: 38°26′53″N 44°33′20″E / 38.44806°N 44.55556°E / 38.44806; 44.55556[1]CountryIranProvinceWest AzerbaijanCountyKhoyDistrictQaturRural DistrictZeriPopulation (2016)[2] • Total1,611Time zoneUTC+3:30 (IRST) Zeri (Persian:...

YOLO!Genre Drama Roman Ditulis oleh Titien Wattimena Katatinut Skenario Beta Ingrid Ayu Obe Karel SutradaraAnnisa MeutiaPemeran Adhisty Zara Jerome Kurnia Michael Olindo Daffa Wardhana Jessica Shaina Penata musikJoseph S. DjafarNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim1Jmlh. episode8ProduksiProduser eksekutif Sutanto Hartono Monika Rudijono Anthony Buncio ProduserWicky V. OlindoSinematografiDian RaishaPenyunting Dinda Amanda Aji Pradityo Eko Purwono Lilik Subagyo Penga...
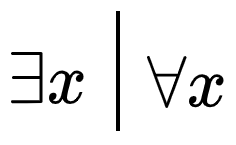











![{\displaystyle \exists !x\,P(x)\equiv \exists x[P(x)\,{\text{et}}\,\forall y(P(y)\Longrightarrow y=x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a9dd30a0a62d5aa434a0f2bc1e4e058abab9cad)









![{\displaystyle {\frac {\exists xF\quad {\begin{array}{c}[F]\\\vdots \\q\end{array}}}{q}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d7e95c83a95a61593725010bb249ab061f92aca)


