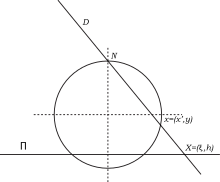
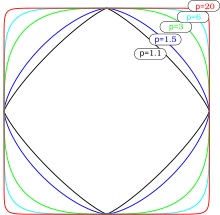
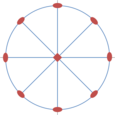
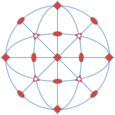
Projection stéréographique
|
Read other articles:
RIMOWAJenisGmbHIndustriPerjalananDidirikan1898PendiriPaul MorszeckKantorpusatKoln, JermanTokohkunciAlexandre Arnault, CEODieter Morszeck, CEOProdukBagasiPemilikLVMH (80%)Situs webwww.rimowa.com Rimowa (pelafalan dalam bahasa Jerman: [ʁɪˈmoːva]), lebih sering ditulis RIMOWA, adalah sebuah produsen bagasi yang didirikan pada tahun 1898, di Koln, Jerman. Pada tahun 2016, RIMOWA bergabung ke LVMH,[1][2] dan menjadi perusahaan asal Jerman pertama yang tergabung ke dalam...

Questa voce o sezione sull'argomento Messico non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Hidalgostato federato(ES) Estado Libre y Soberano de Hidalgo Hidalgo – VedutaSito archeologico di Pahñú LocalizzazioneStato Messico AmministrazioneCapoluogoPachuca GovernatoreJulio Menchaca Salazar (MORENA) dal 5 settembre 2022 Data di istitu...

Neoclassical Grade II* listed building in Liverpool, England For other uses, see Lyceum (disambiguation). The LyceumGeneral informationArchitectural styleNeo-classicalTown or cityLiverpoolCountryEnglandConstruction started1800Completed1802Cost£11,000 (1803)Design and constructionArchitect(s)Thomas HarrisonEngineerWilliam Slater The Lyceum is a Neoclassical Grade II* listed building located on Bold Street, Liverpool. It was constructed in 1802 as a news-room and England's first subscription l...

العلاقات الإكوادورية الإسبانية الإكوادور إسبانيا الإكوادور إسبانيا تعديل مصدري - تعديل العلاقات الإكوادورية الإسبانية هي العلاقات الثنائية التي تجمع بين الإكوادور وإسبانيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدو�...

Untuk kegunaan lain, lihat Oberon (disambiguasi). OberonCitra Oberon yang diabadikan oleh Voyager 2 pada tanggal 24 Januari 1986. Sejumlah kawah tubrukan dapat dilihat. Kawah Hamlet, di bawah bagian tengah, memiliki bahan gelap di dasarnya; di kiri atasnya terdapat kawah Othello yang lebih kecil. Di kiri bawah terdapat gunung setinggi 11 km, kemungkinan puncak tengah kawah lain. Mommur Chasma ada di kanan atas.PenemuanDitemukan olehWilliam HerschelTanggal penemuan11 Januari 1787[...

العلاقات الأوكرانية السورينامية أوكرانيا سورينام أوكرانيا سورينام تعديل مصدري - تعديل العلاقات الأوكرانية السورينامية هي العلاقات الثنائية التي تجمع بين أوكرانيا وسورينام.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدول�...

Sa Ngalan ng Ama, Ina, at mga AnakTheatrical movie posterSutradaraJon VillarinPemeranRobin PadillaMariel RodríguezDaniel PadillaKylie PadillaBela PadillaRJ PadillaMathew PadillaPerusahaanproduksiRCP ProductionsDistributorStar CinemaTanggal rilis 29 Januari 2014 (2014-01-29) NegaraPhilippinesBahasaFilipinoPendapatankotorP 1,280,012.38 Sa Ngalan ng Ama, Ina, at mga Anak (Tagalog: In the Name of the Father, Mother, and Children) adalah afilm aksi Filipina yang disutradarai oleh Jon Villari...

2014 Irish filmA Nightingale FallingFilm posterDirected byGarret DalyMartina McGlynnWritten byGarret DalyMartina McGlynnStory byPj CurtisProduced byGarret DalyMartina McGlynnGerry BurkePj CurtisStarringTara BreathnachMuireann BirdGerard McCarthyBrian FortuneElliot MoriartyAndy KellegherRosemary HendersonMichael James FordMark TankersleyBlathnaid RyanMaura ClancyDerek O'SullivanCinematographyGarret DalyEdited byJames DalyMusic byGraeme StewartProductioncompanyMixed Bag MediaDistributed byGrea...

Extinct Karluk Turkic language of Central Asia Turki redirects here. For other uses, see Turki (disambiguation). ChagataiچغتایČaġatāyChagatai written in Nastaliq script (چغتای)RegionCentral AsiaExtinctAround 1921Language familyTurkic Common TurkicKarlukChagataiEarly formsKarakhanid Khorezmian Writing systemPerso-Arabic script (Nastaliq)Official statusOfficial language in Chagatai Khanate Moghulistan Yarkand Khanate Timurid Empire Mughal Empire Khanate of Khiva[1] Buk...

Scottish recipient of the Victoria Cross Donald CameronLieutenant Donald Cameron in September 1943Born(1916-03-18)18 March 1916Carluke, South LanarkshireDied10 April 1961(1961-04-10) (aged 45)Royal Hospital Haslar, GosportAllegianceUnited KingdomService/branchRoyal NavyYears of service1939–1961RankCommanderCommands heldHMS DolphinHMS X6Battles/warsSecond World War Operation Source AwardsVictoria Cross Commander Donald Cameron, VC (18 March 1916 – 10 April 1961) was a Scotti...

PausMartinus IVAwal masa kepausan22 Februari 1281Akhir masa kepausan8 Maret 1285PendahuluNikolaus IIIPenerusHonorius IVInformasi pribadiNama lahirSimon de BrieLahir1210Touraine, PrancisWafat28 Maret 1285Perugia, Italia Martinus IV, Martinus lahir di Prancis. Dahulu dia bernama Simon de Brion, dari Keuskupan Sens. Terpilih menjadi Paus pada 23 Maret 1281. Ia merupakan Paus kedua yang mempergunakan nama Martinus, tetapi ia memakai urutan IV karena sebelumnya ada dua paus-tandingan yang memakai ...

Medical conditionNaevus flammeus nuchaeOther namesStork bite or Nevus simplexSpecialtyDermatology Naevus flammeus nuchae, or colloquially stork bite, is a congenital capillary malformation present in newborns. It is a common type of birthmark in a newborn.[1] Prevalence and symptoms Stork bites occur in a significant number of newborns, with estimates ranging from 22–40 percent[2] to 40–70 percent;[3] they are reported more frequently for white babies than for infa...

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапси...

Untuk tempat lain yang bernama sama, lihat Pantai (disambiguasi). PantaiDesaNegara IndonesiaProvinsiKalimantan TengahKabupatenKapuasKecamatanKapuas BaratKode Kemendagri62.03.05.2005 Luas45 km²Jumlah penduduk1.334Kepadatan29,64 jiwa/km² Pantai adalah nama desa di wilayah Kecamatan Kapuas Barat, Kabupaten Kapuas, Provinsi Kalimantan Tengah, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Adm...

Longest north–south state highway in New York NY 22 redirects here. The term may also refer to New York's 22nd congressional district. White Plains Post Road redirects here. For the road of a similar name wholly in the Bronx, see White Plains Road. New York State Route 22NY 22 highlighted in redRoute informationMaintained by NYSDOT, NYCDOT, Clinton County, Westchester County, and the cities of Mount Vernon and PlattsburghLength337.26 mi[1] (542.77 km)Existed...

Species of butterfly Acleros ploetzi Acleros ploetzi figure 7 Scientific classification Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Lepidoptera Family: Hesperiidae Genus: Acleros Species: A. ploetzi Binomial name Acleros ploetziMabille, 1890[1] Synonyms Apaustus leucopygus Plötz, 1879 Acleros ploetzi, the Ploetz's dart or Ploetz's dusky skipper, is a butterfly in the family Hesperiidae. It is found in Senegal, the Gambia, Guinea-Bissau, Guinea, Sierra Leone, Liber...

1998 single by KissPsycho CircusSingle by Kissfrom the album Psycho Circus ReleasedAugust 1998Recorded1998StudioA&M Studios & One on One Studios, Los AngelesGenreHeavy metalLength5:30LabelMercury/PolyGram MECP-449 (US)Songwriter(s)Paul Stanley, Curt CuomoProducer(s)Bruce FairbairnKiss singles chronology Jungle (radio edit) / Jungle (full version) (1997) Psycho Circus (1998) We Are One / Psycho Circus (1998) Music videoPsycho Circus on YouTube Psycho Circus is a song by the American ha...

ContrabbassoUn moderno contrabbasso con un arco francese e un pickupInformazioni generaliOrigineItalia InvenzioneXVI secolo Classificazione321.322-71 Cordofoni composti, con corde parallele alla cassa armonica, ad arco FamigliaViole da braccio UsoMusica barocca Musica galante e classica Musica europea dell'Ottocento Musica contemporanea Musica jazz e black music EstensioneIl contrabbasso è uno strumento traspositore d'ottava, le sue note vengono scritte un'ottava più in alto rispetto al suo...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. AtradiusJenisPerusahaan asuransi kredit perdaganganIndustriAsuransiDidirikanNederlandsche Credietverzekering Maatschappij (NCM) pada 1925, Crédito y Caución pada 1929, Gerling-Konzern Speziale Kreditversicherung pada 1954, GERLING NCM pada 2001Kantor...

Pour les articles homonymes, voir Marilyn Manson et Manson. Marilyn Manson Marilyn Manson sur scène à Moscou, en Russie, en 2012.Informations générales Pays d'origine États-Unis Genre musical Metal industriel, rock industriel, metal alternatif, glam rock, shock rock Années actives Depuis 1989 Labels Nothing Records, Interscope Records (1989–2011), Cooking Vinyl (2012-2015), Loma Vista Recordings, Caroline international (2017-2021) Site officiel www.marilynmanson.com Composition du gr...