Primalité dans un anneau
|
Read other articles:

Halaman ini berisi artikel tentang jaringan hipermarket di Indonesia. Untuk supermarket Amerika, lihat Hypermart USA. HypermartIndustriRitelDidirikan15 Januari 2004PendiriMatahari Putra PrimaKantorpusatTangerang, Banten, IndonesiaTokohkunciCamelito J. Regalado (Presiden Direktur)PendapatanRp 13,5 triliun (2016)PemilikMatahari Putra PrimaKaryawan12.585 (2016)Situs webwww.hypermart.co.id Logo Hypermart (2004–2015 dan 2020-2022) Hypermart Mal SKA Pekanbaru Hypermart adalah sebuah jaringan hipe...

1986 South Down by-election← 19831987 →South Down constituency First party Second party Candidate Enoch Powell Eddie McGrady Party Ulster Unionist SDLP Popular vote 24,963 23,121 Percentage 48.4% 44.8 Swing 8.1 5.5% Location of South Down within Northern Ireland MP before election Enoch Powell Ulster Unionist Party Elected MP Enoch Powell Ulster Unionist Party The South Down by-election of 1986 was part of a co-ordinated series of by-elections aimed t...

Murdered Mexican social activist Marisela Escobedo OrtizPlaque indicating the place Ortiz was killedBornJune 12, 1958DiedDecember 16, 2010Chihuahua City, MexicoCause of deathMurderNationalityMexicanOccupation(s)Nurse, market store ownerKnown forSocial activismChildren5 Marisela Escobedo Ortiz[1][2] (June 12, 1958 – December 16, 2010) was a Mexican social activist from Juarez, Chihuahua, who was assassinated while protesting the 2008 murder of her daughter.[3 ...

Сын отца народов Жанры фильм-биография военный фильм драма Режиссёры Сергей Щербин Сергей Гинзбург Сценарист Эдуард Володарский В главных ролях Гела МесхиАнатолий ДзиваевАнатолий ГущинЮрий Лахин Марина Ворожищева Алексей Вертков Композиторы Сергей Морозов Людмила М...

Enlisted rating This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Command master chief petty officer – news · newspapers · books · scholar · JSTOR (May 2008) (Learn how and when to remove this template message) A U.S. command master chief in 2007 gives a tour of USS Ronald Reagan to a Japanese command mas...

كأس بلغاريا 2015–16 تفاصيل الموسم كأس بلغاريا النسخة 94 البلد بلغاريا التاريخ بداية:23 سبتمبر 2015 نهاية:24 مايو 2016 المنظم اتحاد بلغاريا لكرة القدم البطل سسكا صوفيا مباريات ملعوبة 33 عدد المشاركين 32 كأس بلغاريا 2014–15 كأس بلغاريا 2016–17 تعديل مصد...

Spanish political coalition You can help expand this article with text translated from the corresponding article in Spanish. (February 2015) Click [show] for important translation instructions. View a machine-translated version of the Spanish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translat...
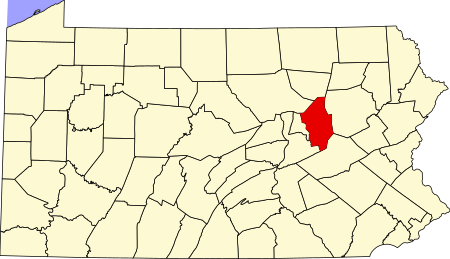
Location of Columbia County in Pennsylvania This is a list of the National Register of Historic Places listings in Columbia County, Pennsylvania. This is intended to be a complete list of the properties and districts on the National Register of Historic Places in Columbia County, Pennsylvania, United States. The locations of National Register properties and districts for which the latitude and longitude coordinates are included below, may be seen in a map.[1] There are 31 properties ...

American politician Isaac McKimBorn(1775-07-21)July 21, 1775Baltimore, Province of Maryland, British AmericaDiedApril 1, 1838(1838-04-01) (aged 62)Baltimore, Maryland, U.S.NationalityAmericanOccupation(s)Politician, MerchantKnown forU.S. Representative from Maryland; owner of the famous Baltimore clipper AnnMcKimSpouseAnn McKim (??-Jan 16, 1875)ChildrenNoneParentJohn McKimRelativesWilliam Duncan (brother); John McKim Jr. (cousin); Alexander McKim (uncle); Isaac McKim (July 21, 1775 ...

Benefit event in Canada This article needs to be updated. Please help update this article to reflect recent events or newly available information. (November 2023) Black & Blue FestivalGenreElectronic dance music, techno, etc.DatesCanadian Thanksgiving weekendLocation(s)MontrealYears active1991-presentFounded byBad Boy Club MontréalAttendance70,000 (2010)WebsiteBlack and Blue Festival Official Website Black and Blue Festival dance festival The Black & Blue Festival is an electronic mu...

Mimi Parent con fratelli e sorelle Maria (Mimi) Parent Benoît (Montréal, 8 settembre 1924 – Ollon, 14 giugno 2005) è stata una pittrice canadese di matrice surrealista. Indice 1 Biografia 2 Alcune opere 3 Esposizioni principali 4 Note 5 Bibliografia 6 Voci correlate 7 Collegamenti esterni Biografia Marie Parent, detta Mimi, era l'ottava dei nove figli dell'architetto Lucien Parent (1893-1956). Dopo la scuola dell'obbligo presso il convento delle Dames du Sacré-Cœur,[1] dal 1942...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Technology demonstrations and projects developed by Nintendo Video gameSuper Mario 128Super Mario 128 as shown at the Space World event in August 2000Publisher(s)NintendoDirector(s)Yoshiaki KoizumiSeriesMarioPlatform(s)GameCubeGenre(s)Technology demonstration Super Mario 128 was a codename for two different development projects at Nintendo. The name was first used in 1997 for a sequel to Super Mario 64 for the 64DD, which was canceled. The name was reused for a GameCube tech demo at the Ninte...

Ancient Egyptian temple complex Not to be confused with Temple of Dendur. The Dendera Temple complex (Ancient Egyptian: Iunet or Tantere; the 19th-century English spelling in most sources, including Belzoni, was Tentyra; also spelled Denderah[1]) is located about 2.5 kilometres (1.6 mi) south-east of Dendera, Egypt. It is one of the best-preserved temple complexes of ancient Egypt. The area was used as the sixth nome of Upper Egypt, south of Abydos. Temple of Hathor, Dendera Desc...

Giovanni VergaLahir(1840-09-02)2 September 1840Catania, Sicily, Italy1Meninggal27 Januari 1922(1922-01-27) (umur 81)Catania, Sicily, ItalyPekerjaanWriterKebangsaanItalianAliran sastraRealism Halaman artikel ini diterjemahkan, sebagian atau seluruhnya, dari halaman di (Tolong cantumkan kode bahasa Wiki sumber terjemahan) yang berjudul (Tolong cantumkan nama artikel sumber terjemahan). Lihat pula [{{localurle:{{{1}}}:|oldid=&action=history}} sejarah suntingan halaman aslinya] untu...

Hak asasi manusiaLogo hak asasi manusia Kategorisasi Hak sipil dan politikHak ekonomi, sosial, dan budayaTiga generasi HAM Instrumen utama PUHAMICCPRICESCR Instrumen regional EropaAmerikaAfrika Hari Hak Asasi Manusialbs Hak asasi manusia di Malaysia adalah bersifat kontroversial dengan adanya berbagai tuduhan pelanggaran hak asasi manusia di negeri ini. Kelompok hak asasi manusia dan pemerintah asing umumnya kritis terhadap pemerintah Malaysia dan Kepolisian diraja Malaysia. hukum penah...

1936–1938 campaign in the Soviet Union This article may require copy editing for grammar, style, cohesion, tone, or spelling. You can assist by editing it. (November 2023) (Learn how and when to remove this message) This article is about the 1936–1938 Soviet purge. For political purges in general, see Purge. For the period of the French Revolution, see Reign of Terror. For other uses, see Great Terror (disambiguation). ‹ The template Infobox civilian attack is being considered for ...

「玉林」重定向至此。关于其他用法,请见「玉林 (消歧义)」。 玉林市壯語:Yoglinz地级市市政府驻地玉林市的地理位置(黄色部分)坐标:22°39′14″N 110°10′52″E / 22.654°N 110.1811°E / 22.654; 110.1811国家 中华人民共和国自治區广西壮族自治区設立1997年4月22日政府駐地玉州区下级行政区2市辖区、4县、1县级市政府 • 市委書記王琛 •&#...

ستاكيفيل الإحداثيات 43°26′13″N 92°46′59″W / 43.436944444444°N 92.783055555556°W / 43.436944444444; -92.783055555556 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة ميتشل خصائص جغرافية المساحة 1.387499 كيلومتر مربع1.387497 كيلومتر مربع (1 أبريل 2010) ارتف�...

Эта статья — о коммуне во Франции. О числительном см. 1 (число). КоммунаРазRaze Герб 47°35′01″ с. ш. 6°00′41″ в. д.HGЯO Страна Франция Регион Франш-Конте Департамент Верхняя Сона Кантон Се-сюр-Сон-э-Сент-Альбен Мэр Жоэль Жанньо(2008—2014) История и география Пло...