Noyau de la chaleur
|
Read other articles:

Artikel ini bukan mengenai Universitas Semarang.Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Universitas Negeri Semarang – berita · surat kabar · buku · cendekiawan · JSTORartikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasa...

Médaille MurchisonLa médaille Murchinson.PrésentationType Médaille, prix scientifique (d)Fondation 1873Site web (en) www.geolsoc.org.uk/About/History/Award-Winners-Since-1831/Murchison-MedalLocalisationLocalisation Royaume-Unimodifier - modifier le code - modifier Wikidata Ne doit pas être confondu avec Prix Murchison. La médaille Murchison est une récompense scientifique dans le domaine de la géologie décernée par la Geological Society of London. La médaille est nommée...

الاتحاد الاجتماعي المسيحي في بافاريا Christlich-Soziale Union in Bayern CSU البلد ألمانيا التأسيس تاريخ التأسيس 1945؛ منذ 79 سنوات (1945) حزب الشعب البافاري(ليس سلف قانوني) الشخصيات الرئيس ماركوس زودر عدد الأعضاء ▼ 132.000 (حسب عام 2022) المقر الرئيسي ميونخ مقر الحزب ميونخ، بافا...

Artahsasta IVKemungkinan gambar dari Artahsasta IV yang mengenakan mahkota FiraunRaja Diraja IranFiraun MesirBerkuasa338–336 SMPendahuluArtahsasta IIIPenerusDarius IIIInformasi pribadiKematian336 SMNama takhtaArtahsasta IVAyahArtahsasta IIIIbuAtosaAgamaZoroastrianisme Arsyaka, dikenal dengan nama takhtanya Artahsasta IV, adalah Raja Diraja (Kaisar) Iran dan Firaun Mesir dari Dinasti Akhemeniyah, berkuasa pada tahun 338 sampai 336 SM. Dia mewarisi takhta sepeninggal ayahnya, Artahsasta I...

Interjet IATA ICAO Kode panggil - AIJ ABC AEROLINEAS Didirikan2005PenghubungBandar Udara Internasional Lic. Adolfo López MateosKota fokusBandar Udara Internasional General Mariano EscobedoBandar Udara Internasional Don Miguel Hidalgo y CostillaArmada27Tujuan13Kantor pusatToluca, MeksikoTokoh utamaJose Luis Graza Alvarez (CEO)Situs webhttp://www.interjet.com.mx Sukhoi Superjet 100; Campeche, Mexico Interjet merupakan sebuah maskapai penerbangan bertarif rendah yang berbasis di Toluca, Meksiko...

American politician (1805–1861) Matthias WardUnited States Senatorfrom TexasIn officeSeptember 27, 1858 – December 5, 1859Appointed byHardin Richard RunnelsPreceded byJames P. HendersonSucceeded byLouis WigfallMember of the Texas Senatefrom the 1st districtIn officeNovember 13, 1849 – November 3, 1850Preceded byWilliam M. Buckskin WilliamsSucceeded byJoseph H. Burks Personal detailsBorn(1805-10-13)October 13, 1805Elbert County, Georgia, U.S.DiedOctober 5, 1861(1861-10-...

For other ships with the same name, see SS Leonardo da Vinci. SS Leonardo da Vinci in Port Everglades, 1975 History NameLeonardo da Vinci NamesakeLeonardo da Vinci Owner 1960–1977: Italian Line 1977–1982: Italia Crociere[1] Operator 1960–1976: Italian Line 1976–1977: laid up 1977–1978: Italia Crociere 1978–1982: laid up[1][2] Port of registryGenoa, Italy[1] BuilderAnsaldo Shipyards, Genoa, Italy Yard number1550[1] Laid down1958[2&#...
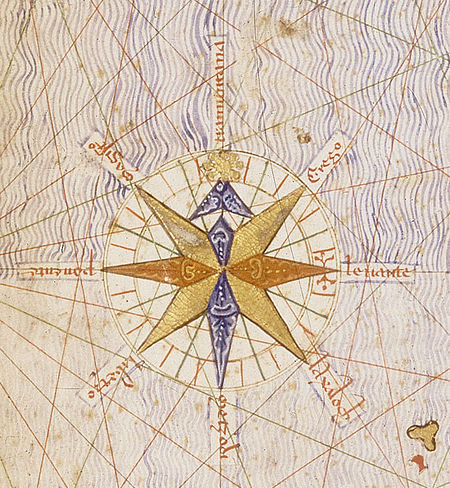
1375 world map Montage of 8 pages (the third to sixth leaves) of the original 1375 Catalan Atlas Detail of the Catalan Atlas, the first compass rose depicted on a map The Catalan Atlas (Catalan: Atles català, Eastern Catalan: [ˈatləs kətəˈla]) is a medieval world map, or mappa mundi, probably created in the late 1370s or the early 1380s (often conventionally dated 1375),[1][2] that has been described as the most important map of the Middle Ages in the Catalan lan...

Cryptocrystalline form of the mineral quartz This article is about the sedimentary rock. For other uses, see Flint (disambiguation). FlintSedimentary rockA sample of Miorcani flint from the Cenomanian chalky marl layer of the Moldavian Plateau (c. 7.5 cm (3.0 in) wide)CompositionCryptocrystalline quartz A piece of flint 9–10 cm (3.5–3.9 in) long, weighing 171 grams Flint, occasionally flintstone, is a sedimentary cryptocrystalline form of the mineral quartz,...

Teritori Dependen Kaldea (atau Patriarkal Dependen) pada Patriark di Yordania adalah sebuah yurisdiksi pra-keuskupan misionaris dari Gereja Katolik Kaldea sui iuris (Katolik Timur: Ritus Kaldea, bahasa Suryani) yang meliputi (Trans)Yordania. Sebagai Dependen Teritori pada Patriark, wilayah gerejawi tersebut adalah subyek langsung dari Patriark Katolik Kaldea Babilonia (sebetulnya di Baghdad, Irak), tanpa menjadi bagian dari provinsi gerejawi manapun. Wilayah gereja tersebut tak menggelari Usk...

School in AustraliaCronulla High SchoolLocationCronulla in Southern Sydney, New South Wales,AustraliaCoordinates34°02′21″S 151°09′29″E / 34.0390935°S 151.158126°E / -34.0390935; 151.158126InformationTypeGovernment-funded co-educational comprehensive and specialist secondary day schoolMottoLatin: Caritas Humilitas Dignitas(Charity Humility Dignity)Established1961; 63 years ago (1961)School districtSutherland; Metropolitan SouthEducational ...

الملك الكوشي في نبتة ومروي مصر شباكا نقش للملك شباكا من الكرنك الملك الكوشي في نبتة ومروي مصر مرافق الملكة كلهاتا، الملكة ميسبات ، الملكة تبيك نيمون ؟ معلومات شخصية الاسم الكامل شباكا نفركار' تاريخ الميلاد القرن 8 ق.م تاريخ الوفاة 707 or 706 ق.م مكان الدفن مدينة الكرو (الهرم -...

Concept in philosophy, religion, rhetoric, and psychology For other uses, see Logos (disambiguation). Greek spelling of logos Logos (UK: /ˈloʊɡɒs, ˈlɒɡɒs/, US: /ˈloʊɡoʊs/; Ancient Greek: λόγος, romanized: lógos, lit. 'word, discourse, or reason') is a term used in Western philosophy, psychology and rhetoric, as well as religion (notably Christianity); among its connotations is that of a rational form of discourse that relies on inductive and deductive reas...

Confessional Baptist Association (CBA)AbbreviationCBAFormation1997 (1997)HeadquartersMansfield, TexasModeratorCorey SmithWebsitecba1689.comFormerly calledAssociation of Reformed Baptist Churches in America (ARBCA) Part of a series onBaptists Background Christianity Protestantism Puritanism Anabaptism Doctrine Baptist beliefs Confessions Believers' Church Priesthood of all believers Individual soul liberty Separation of church and state Sola scriptura Congregationalism Ordinances Offices...

Colombian cross-country mountain biker This article needs to be updated. Please help update this to reflect recent events or newly available information. (January 2019) Laura Abril (2015) Laura Valentina Abril Restrepo (born 28 January 1990, La Cumbre) is a Colombian cross-country mountain biker.[1][2] She was junior world champion in 2008.[3] At the 2012 Summer Olympics, she competed in the Women's cross-country at Hadleigh Farm, but didn't complete the race. Laura Ab...

Destroyer of the Royal Navy HMS Vanquisher off Portsmouth, England, during World War II. History United Kingdom NameHMS Vanquisher NamesakeVanquisher OperatorRoyal Navy Ordered30 June 1916[2] BuilderJohn Brown & Company, Clydebank[1] Laid down27 September 1916[1] Launched18[1] or 28[2] August 1917 Commissioned2 October 1917[2] DecommissionedJune 1945[1] IdentificationPennant number: D54 MottoPugna vinco pugno (I fight, I conquer with...

此生者传记没有列出任何参考或来源。 (2015年6月3日)请协助補充可靠来源,针对在世人物的无法查证的内容将被立即移除。 娜斯蒂亞·柳金Nastia Liukin柳金在2009年个人资料全名Anastasia Valeryevna Liukin昵称Nastia代表国家 美国出生 (1989-10-30) 1989年10月30日(34歲) 苏联俄羅斯莫斯科籍贯 美国得克萨斯州Parker身高5英尺3英寸(1.60米)比赛项目女子競技體操级别Senior Internation...

Music genre This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Southern soul – news · newspapers · books · scholar · JSTOR (July 2016) (Learn how and when to remove this message) Southern soulStylistic originsSoulbluescountryrhythm and bluesgospelCultural originsLate 1950s, Southern United StatesDerivative form...

Radio station in Oakley–Salt Lake City, Utah KNAHOakley, UtahBroadcast areaSalt Lake City metropolitan areaFrequency101.5 MHzBranding101.5 Hank FMProgrammingFormatCountry musicOwnershipOwnerBroadway Media(Broadway Media LS, LLC)Sister stationsKXRKKYMVKUDDKALLKOVOKUUUHistoryFirst air dateJune 28, 2000; 24 years ago (2000-06-28)Former call signsKPKK (2000–2003)KKIK (2003)KEGA (2003–2023)Call sign meaningHankTechnical information[1]Licensing authorityFCCFacility I...

Place in Upper Carniola, SloveniaSpodnja SoricaSpodnja SoricaLocation in SloveniaCoordinates: 46°13′4.74″N 14°1′58.99″E / 46.2179833°N 14.0330528°E / 46.2179833; 14.0330528Country SloveniaTraditional RegionUpper CarniolaStatistical regionUpper CarniolaMunicipalityŽeleznikiElevation783.5 m (2,570.5 ft)Population (2002) • Total102[1] Spodnja Sorica (pronounced [ˈspoːdnja ˈsoːɾitsa]; German: Unterzarz[2]...





























![{\displaystyle \Re \mathrm {e} \left[\,s\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bffe1c305e564037b811a79ad55d99100521c8f)



![{\displaystyle \mathrm {det} \ {\hat {H}}\ =\ \exp \,\left[\,-\ \zeta '(0)\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bff617a26f9ed66d74433f588489860e657176b)









