Nombre de Thue
|
Read other articles:

Tari TopengPertunjukan drama tari Topeng Bali Bagian dari seri Drama tari di Asia Tenggara Topografi Asia Tenggara Myanmar Yama Zatdaw Kamboja Khmer_shadow_theatre Lakhon Khol Lakhon Mohory Lakhon Pol Srey Royal Ballet of Cambodia Yike Indonesia Bangsawan Barong Gambuh Kecak Ketoprak Kuda Lumping Legong Lenong Ludruk Mak yong Sendratari Ramayana Randai Reog Ronggeng Sandiwara Toneel Topeng Wayang wong Laos Classical dance and theatre Malaysia Bangsawan Boria Dikir Barat Jikey Kuda Lumping Mak...

1996 novel by Neal Stephenson and J. Frederick George The Cobweb First editionAuthorNeal Stephenson and J. Frederick GeorgeCover artistWalter BibikowLanguageEnglishGenreScience fiction novelPublisherBantam Spectra (U.S.A.)Publication date1996Media typePrint (Hardcover & Paperback) The Cobweb is a 1996 novel written by Neal Stephenson with J. Frederick George, a pseudonym for Stephenson's uncle, historian George Jewsbury. It was originally published under the collective pseudonym...

House elections in Washington See also: 2020 Washington elections 2020 United States House of Representatives elections in Washington ← 2018 November 3, 2020 2022 → All 10 Washington seats to the United States House of Representatives Majority party Minority party Party Democratic Republican Last election 7 3 Seats won 7 3 Seat change Popular vote 2,340,356 1,545,436 Percentage 59.34% 39.18% Swing 3.16% 4.48% Democratic 40–...

1956 studio album by Woody GuthrieSongs to Grow on for Mother and ChildStudio album by Woody GuthrieReleased1956Recorded1947GenreFolkchildren's musicLabelFolkways RecordsAlternative CoverThe 1991 reissue cover. Professional ratingsReview scoresSourceRatingAllmusic[1] Songs to Grow on for Mother and Child is a collection of children's music by folk singer Woody Guthrie. Recorded in 1947 and first released in 1956 by Folkways Records, a remastered recording was issued by Smithso...

Into the FlamesPoster promosi untuk Into the FlamesGenreDrama sejarahDitulis olehJung Sung-hee Lee Han-hoSutradaraKim Sang-raePemeranChoi Soo-jong Ryu Jin Son Tae-young Lee In-hyeNegara asalKorea SelatanBahasa asliKoreaJmlh. episode20ProduksiProduser eksekutifChoi Byung-hwaProduserJung Hoe-seok Lee Kyung-seon Jung Hyung-seoLokasi produksiKoreaDurasiJumat dan Sabtu pukul 23:00 (WSK)Rumah produksiKangho ProductionRilis asliJaringanTV ChosunRilis25 April (2014-04-25) –28 Juni 2014&#...

Denis PodalydèsDenis Podalydès at the 2018 Cannes Film FestivalLahir22 April 1963 (umur 61)Versailles, PrancisPekerjaanPemeranTahun aktif1988-kini Denis Podalydès (lahir 22 April 1963) adalah seorang pemeran dan penulis naskah Prancis berdarah Yunani.[1] Podalydès tampil dalam 80 film sejak 1989. Ia membintangi The Officers' Ward, yang masuk Festival Film Cannes 2001.[2] Referensi ^ Greek-French Actor Denis Podalydès Stars as Sarkozy in La Conquête. greekrepor...

Chinese computer technology company Insyde Software系微公司Company typePublicTraded asTPEx: 6231IndustryComputer industryFoundedSeptember 18, 1998; 25 years ago (1998-09-18)FounderJeremy Wang, Jonathan JosephHeadquartersTaipei, TaiwanProducts BIOS/UEFI Firmware EC Firmware BMC Firmware InsydeH2O Supervyse BlinkBoot RevenueNT$959,482,000Websitewww.insyde.com Insyde Software (Chinese: 系微公司; pinyin: Xìwēi Gōngsī) is a company that specializes in UEFI sys...

Metric of scholarly journals SCImago redirects here. Not to be confused with SCImago Institutions Rankings. Portal SCImago Journal & Country Rank screenshot Part of a series onCitation metrics Altmetrics Article-level Author-level Eigenfactor G-index H-index Bibliographic coupling Citation Analysis Dynamics Index Graph Co-citation Proximity Analysis Coercive citation Citation cartel I4OC Journal-level CiteScore Impact factor SCImago Kardashian Index vte The SCImago Journal Rank (SJR) indi...

American trade union This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. See Wikipedia's guide to writing better articles for suggestions. (February 2020) (Learn how and when to remove this message) This article needs additional citations for verification. Please help improve this article by adding citations...

هداية الحيارى في أجوبة اليهود والنصارى هداية الحيارى في أجوبة اليهود والنصارى غلاف النسخة العربية من الكتاب معلومات الكتاب المؤلف ابن قيم الجوزية اللغة العربية التقديم نوع الطباعة ورقي غلاف عادي ويكي مصدر هداية الحيارى - ويكي مصدر تعديل مصدري - تعديل هداية ال...

33°46′22″N 84°21′58″W / 33.7728°N 84.3661°W / 33.7728; -84.3661 Mixed-use development in Georgia, United StatesPonce City MarketPonce City Market under renovation in May 2012Former namesSears, Roebuck and Co. Mail-Order Warehouse and Retail Store; City Hall EastGeneral informationTypeMixed-use developmentArchitectural styleLate 19th and 20th Century RevivalsAddress675 Ponce de Leon Ave. NETown or cityAtlanta, GeorgiaCountryUnited StatesInaugurated1926Renov...
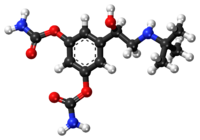
Chemical compound BambuterolBambuterol (top),and (R)-bambuterol (bottom)Clinical dataAHFS/Drugs.comInternational Drug NamesPregnancycategory Unknown Routes ofadministrationOral (tablets)ATC codeR03CC12 (WHO) Legal statusLegal status AU: S4 (Prescription only) In general: ℞ (Prescription only) Pharmacokinetic dataBioavailability20%MetabolismExtensive hepatic.Further metabolized to terbutaline by plasma cholinesteraseElimination half-life13 hours (bambuterol)21 hours ...

British anarchist (1913–1990) John HewetsonPhoto of Hewetson published in 1945BornJohn Christopher Hewetson(1913-01-10)10 January 1913Birmingham, EnglandDied20 December 1990(1990-12-20) (aged 77)Surrey, EnglandEducation Shrewsbury School Magdalen College, Oxford Occupations Physician Writer Editor MovementAnarchismPartner Peta Edsall Phyllis John Christopher Hewetson (10 January 1913 – 20 December 1990) was a British anarchist physician, writer and newspaper editor.[1][2&...

Fourth century Roman grammarian and teacher of rhetoric from Nuremberg Chronicle Aelius Donatus (English: /doʊˈneɪtəs/; fl. mid-fourth century AD) was a Roman grammarian and teacher of rhetoric. He once taught Jerome,[1] an early Christian Church father who is most known for his translation of the Bible into Latin, known as the Latin Vulgate. Newer revisions of the Vulgate are still in common use by the Catholic Church. Works He was the author of a number of professional works, of...

Music term For the Windows application, see Groove Music. Funk music such as the type performed by groups like Parliament Funkadelic uses catchy electric bass lines and drum patterns to create a propulsive, emphatic rhythmic feel that is often referred to as a groove. In music, groove is the sense of an effect (feel) of changing pattern in a propulsive rhythm or sense of swing. In jazz, it can be felt as a quality of persistently repeated rhythmic units, created by the interaction of the musi...

Bahasa Prancis Quebec Français québécois Dituturkan diQuebec (sebagian besar), New Brunswick, Ontario, Kanada Barat, New EnglandPenutur6,2 juta di Quebec; 700.000 di wilayah Kanada lainnya dan Amerika Serikat (2006)[1] Rincian data penutur Jumlah penutur beserta (jika ada) metode pengambilan, jenis, tanggal, dan tempat.[2] 7.303.740 (Bahasa ibu, 2016) Rumpun bahasaIndo-Eropa ItalikRomanRoman BaratGallo-RomanGallo-RhaetianOïlPrancisPrancis KanadaPrancis Quebec Sta...

2007 wildfire in Southern California Zaca FireAn active flame front of the fireDate(s)July 4, 2007 (2007-07-04) –October 29, 2007 (2007-10-29)LocationSan Rafael Mountains,Los Padres N.F.,Santa Barbara County,CaliforniaCoordinates34°42′57″N 119°46′58″W / 34.7159°N 119.7828°W / 34.7159; -119.7828Statistics[1]Burned area240,207 acres (972 km2)ImpactsDeaths0Non-fatal injuries43Structures destroyed1Damage$118.3 millio...

Cet article est une ébauche concernant la musique électronique et une compositrice belge. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Annette Vande GorneBiographieNaissance 6 janvier 1946 (78 ans)CharleroiNationalité belgeFormation Conservatoire royal de MonsUniversité libre de BruxellesConservatoire royal de BruxellesConservatoire national supérieur de musique et de danse de ParisActivité Composi...

Tendency to adopt group beliefs and behaviors Not to be confused with Herd behavior. Herd mentality is the tendency for people’s behavior or beliefs to conform to those of the group they belong to. The concept of herd mentality has been studied and analyzed from different perspectives, including biology, psychology and sociology. This psychological phenomenon can have profound impacts on human behavior. Social psychologists study the related topics of collective intelligence, crowd wisdom, ...

American shot putter (born 1999) Adelaide AquillaPersonal informationBorn (1999-03-03) March 3, 1999 (age 25)Westlake, Ohio, U.S.SportCountryUnited StatesSportAthleticsEventShot putAchievements and titlesPersonal best(s)Shot put: 19.64m (Eugene, 2022) Medal record Women's athletics Representing United States Pan American Games 2023 Santiago Shot put Adelaide Aquilla (pronounced ah-quill-ah, born March 3, 1999) is an American athlete who specialises in the shot put.[1] Early...




