Mesure régulière

Cet article est une ébauche concernant les mathématiques.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

En théorie de la mesure, une mesure régulière est une mesure sur un espace topologique séparé mesuré qui vérifie deux propriétés qui lient mesure et topologie.

Quelques énoncés qui posent des conditions topologiques assez couramment remplies permettent de garantir la régularité d'une mesure de Borel.

Définition

Une mesure (positive) définie sur une tribu contenant la tribu borélienne d'un espace séparé X est dite régulière lorsqu'elle est à la fois intérieurement régulière et extérieurement régulière[1], c'est-à-dire lorsque :

  1. pour tout élément de la tribu,  ;
  2. pour tout élément de la tribu, .

Variantes

Diverses sources exigent en outre d'une « mesure régulière » d'être une mesure de Borel[2].

Des conditions topologiques qui garantissent la régularité

Deux résultats assurent la régularité des mesures sur deux grandes familles d'espaces.

Théorème : sur un espace localement compact dans lequel tout ouvert est σ-compact, toute mesure de Borel est régulière[3].

La condition topologique de ce théorème peut paraître assez technique, mais elle est entraînée par des hypothèses plus familières : ainsi peut-on vérifier qu'elle sera remplie par un espace localement compact séparé à base dénombrable[4], et a fortiori par un espace métrique compact[5].

Théorème : sur un espace polonais toute mesure borélienne finie est régulière[6].

Références

  1. ↑ (en) Laurent Schwartz, Analyse : Calcul intégral, t. III, Hermann, (ISBN 978-2-7056-6163-2 et 2-705-66163-8), p. 173.
  2. ↑ Ainsi (en) Charalambos D. Aliprantis et Kim C. Border, Infinite Dimensional Analysis : A Hitchhiker's Guide, Springer, , 703 p. (ISBN 978-3-540-32696-0, lire en ligne), p. 435 ou Serge Lang, Real and Functional Analysis, Berlin, Springer, 2007 (ISBN 3540940014), p. 256-257.
  3. ↑ Walter Rudin, Analyse réelle et complexe [détail des éditions], th. 2-18, p. 48.
  4. ↑ (en) Heinz Bauer, Measure and Integration Theory, Walter de Gruyter, coll. « De Gruyter Studies in Mathematics » (no 26), , 230 p. (ISBN 978-3-11-016719-1, lire en ligne), p. 184.
  5. ↑ Schwartz 1993, p. 186. La preuve donnée par cette source ne repose pas sur le théorème mentionné ici mais sur la régularité extérieure de toute mesure finie sur un espace métrique.
  6. ↑ Aliprantis et Border 2007, p. 438.

Read other articles:

Virus hanta

Virus hanta Orthohantavirus Komposisi genom virus ICTVnegative-sense single strand RNA virus (en) TaksonomiSuperdomainBiotaDomainVirusOrdoBunyaviralesFamiliHantaviridaeGenusOrthohantavirus Tipe taksonomiHantaan orthohantavirus Tata namaSinonim taksonVirus Hanta Spesies Andes orthohantavirus Asama orthohantavirus Asikkala orthohantavirus Bayou orthohantavirus Black Creek Canal orthohantavirus Bowe orthohantavirus Bruges orthohantavirus Cano Delgadito orthohantavirus Cao Bang orthohantavirus Ch...

 

New Amsterdam FC

Soccer clubNew Amsterdam FCFull nameNew Amsterdam Football ClubNickname(s)The CannonsFoundedApril 20, 2020; 3 years ago (2020-04-20)Dissolved2022StadiumHofstra University Soccer StadiumHempstead, New YorkCapacity1,600OwnerLaurence GirardLeagueNational Independent Soccer AssociationFall 20214th PlaceWebsiteClub website Home colors Away colors Third colors Current season New Amsterdam Football Club was an American professional soccer club based in Hempstead, New York, that pr...

 

Quinchao

This article is about the commune. For the island, see Quinchao Island. Commune in Los Lagos, ChileQuinchaoCommune Coat of arms Location of Quinchao in the Los Lagos Region QuinchaoLocation in ChileCoordinates: 42°28′15″S 73°29′30″W / 42.47083°S 73.49167°W / -42.47083; -73.49167CountryChileRegionLos LagosProvinceChiloéSeatAchaoGovernment[1] [2] • TypeMunicipality • AlcaldeSantiago Torres Águila (ILC)Area[3]&...

Abu Dhabi

Abu Dhabi أبو ظبي Abū ẓabīKotaAbu Dhabi BenderaEmiratAbu DhabiPemerintahan • JenisMonarki konstitusional [1] • SheikhMuhammad bin Zayid Al NahyanLuas • Total67.340 km2 (26,000 sq mi)Populasi (2013) • Total921.000 • Kepadatan9.221,9/km2 (238,850/sq mi)Zona waktuUTC+4 (Waktu Standar UEA)Situs webAbu Dhabi Government Portal Abu Dhabi Abu Dhabi (Bahasa Arab: أبوظبي ʼAbū Ẓaby, Bahasa In...

 

الفريضة الغائبة (كتاب)

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) الفريضة الغائبة الجهاد الفريضة الغائبة معلومات الكتاب المؤلف محمد عبد السلام فرج البلد مصر اللغة اللغة �...

 

Poisonous fish

Fish containing indigestible toxins Puffer fish are the most poisonous fish in the world. Poisonous fish are fish that are poisonous to eat. They contain toxins which are not destroyed by the digestive systems of animals that eat the fish.[1] Venomous fish also contain toxins, but do not necessarily cause poisoning if they are eaten, since the digestive system often destroys their venom.[1] Examples Species of puffer fish (the family Tetraodontidae) are the most poisonous in t...

Lu e Cuccaro Monferrato

Questa voce sull'argomento centri abitati della provincia di Alessandria è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Lu e Cuccaro MonferratocomuneLu e Cuccaro Monferrato – VedutaPanorama LocalizzazioneStato Italia Regione Piemonte Provincia Alessandria AmministrazioneSindacoFranco Alessio (lista civica) dal 26-5-2019 TerritorioCoordinate44°59′50″N 8°28′20″E / 44.997222°N 8.472222°E44.997222; 8...

 

Fleuve Noir Anticipation

Pour les articles homonymes, voir Fleuve Noir et FNA. Logo des éditions Fleuve Noir entre 1967 et 1977 Le FNA période fusée, le FNA période blanche, puis une partie des suites... ...ultérieures. Fleuve Noir Anticipation (FNA) est une collection consacrée à la science-fiction qui fut créée en septembre 1951 par l'éditeur Fleuve Noir. Elle visait un public populaire et privilégiait le space opera et les sujets grand public[1]. Elle eut une durée de vie exceptionnelle et publia deux...

 

باري ليفنسون

باري ليفنسون (بالإنجليزية: Barry Levinson)‏  معلومات شخصية الميلاد 6 أبريل 1942 (العمر 82 سنة)بالتيمور، ماريلاند، الولايات المتحدة مواطنة الولايات المتحدة  الزوجة فاليري كورتن (1975–1982)  الأولاد سام ليفنزون[1]  الحياة العملية التعلّم الجامعة الأميركية المهنة مخرج اللغة...

تعليم ديني

تعليم دينيمعلومات عامةصنف فرعي من تعليم المُؤَلِّف Richard Dehmel (en) يدرسه religion didactics (en) يمارسها religious education teacher (en) رمز تصنيف البرامج التعليمية 39.0439.0401 تعديل - تعديل مصدري - تعديل ويكي بيانات السجناء المدانين يتلقون التعليم القرآني في فيصل آباد بالسجن المركزي،باكستان في عام 2010 يس�...

 

Andi Abdul Aziz (TNI AL)

Andi Abdul Aziz Kepala Staf Koarmada IIMasa jabatan27 Juni 2022 – 26 Juni 2023PendahuluRachmad JayadiPenggantiIsswarto Informasi pribadiLahir14 Juli 1969 (umur 54)Selayar, Sulawesi SelatanAlma materAkademi Angkatan Laut (1992)Karier militerPihak IndonesiaDinas/cabang TNI Angkatan LautMasa dinas1992—sekarangPangkat Laksamana Muda TNINRP10344/PSatuanKorps PelautSunting kotak info • L • B Laksamana Muda TNI Andi Abdul Aziz, S.H., M.M. (lahir 14 Juli 1969...

 

Maren Lundby

Norwegian ski jumper (born 1994) Maren LundbyLundby in Hinzenbach, 2017CountryNorwayBorn (1994-09-07) 7 September 1994 (age 29)Gjøvik, NorwayHeight1.72 m (5 ft 8 in)Ski clubKolbu KKPersonal best216.5 m (710 ft) Vikersund, 19 March 2023World Cup careerSeasons 2012–2021 2023 Starts148Podiums62Wins30Overall titles3 (2018, 2019, 2020) Medal record Women's ski jumping Representing  Norway Olympic Games 2018 Pyeongchang Individual NH World Champi...

After Band

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: After Band – berita · surat kabar · buku · cendekiawan · JSTOR After BandLahirBandung, IndonesiaGenrePop, RockTahun aktif2004 - sekarangLabelNagaswaraAnggotaRizalMaliaFerryFirmanGaffy After merupakan seb...

 

1851 in the United States

List of events ← 1850 1849 1848 1851 in the United States → 1852 1853 1854 Decades: 1830s 1840s 1850s 1860s 1870s See also: History of the United States (1849–1865) Timeline of United States history (1820–1859) List of years in the United States 1851 in the United States1851 in U.S. states States Alabama Arkansas California Connecticut Delaware Florida Georgia Illinois Indiana Iowa Kentucky Louisiana Maine Maryland Massachusetts Michigan Mississippi Missouri New Hampshire New ...

 

Ministers and elders of the Church of Scotland

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ministers and elders of the Church of Scotland – news · newspapers · books · scholar · JSTOR (February 2023) (Learn how and when to remove this message)Leaders of Church of Scotland congregations The Ordination of Elders in a Scottish Kirk, painting by John Henry Lorimer, 1891 A...

Microprocessor chronology

Progress of miniaturisation, and comparison of sizes of semiconductor manufacturing process nodes with some microscopic objects and visible light wavelengths 1970s The first chips that could be considered microprocessors were designed and manufactured in the late 1960s and early 1970s, including the MP944 used in the F-14 Central Air Data Computer.[1] Intel's 4004 of 1971 is widely regarded as the first commercial microprocessor.[2] Designers predominantly used MOSFET transis...

 

Marcelo Ebrard

Mexican politician (born 1959) In this Spanish name, the first or paternal surname is Ebrard and the second or maternal family name is Casaubón. You can help expand this article with text translated from the corresponding article in Spanish. (July 2023) Click [show] for important translation instructions. View a machine-translated version of the Spanish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must...

 

Nussa (film)

NussaPoster resmiSutradaraBony WirasmonoProduser Anggia Kharisma Ricky Manoppo Skenario Muhamad Nurman Wardi Widya Arifianti Cerita Bony Wirasmono Chrisnawan Martantio Anggia Kharisma M. Irfan Ramli BerdasarkanNussaoleh Ricky ManoppoPemeran Muzakki Ramdhan Aysha Raazana Ocean Fajar Ali Fikry Malka Hayfa Asy'ari Widuri Puteri Fenita Arie Alex Abbad Maudy Koesnaedi Raisa Dewi Sandra Asri Welas Perusahaanproduksi The Little Giantz Visinema Pictures Tanggal rilis 8 Juli 2021 (2021-07-08) ...

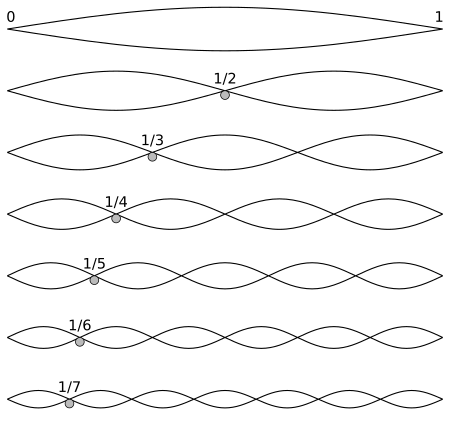
Harmonic series (music)

Sequence of frequencies Harmonics of a string showing the periods of the pure-tone harmonics (period = 1/frequency) A harmonic series (also overtone series) is the sequence of harmonics, musical tones, or pure tones whose frequency is an integer multiple of a fundamental frequency. Pitched musical instruments are often based on an acoustic resonator such as a string or a column of air, which oscillates at numerous modes simultaneously. At the frequencies of each vibrating mode, waves travel i...

 

岐阜城

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方）出典検索?: 岐阜城 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2019年10月) logo岐阜城（岐阜県） 金華山の山上にある模擬天守�...