Matériau main gauche
| |||||||||||||||||||||||||||||||||||||||
Read other articles:

Harimau Champawat lbs Harimau Champawat adalah seekor harimau bengal betina yang bertanggung jawab atas kematian sekitar 436 jiwa di Nepal dan wilayah Kumaon di India, selama tahun-tahun akhir abad ke-19 dan tahun-tahun pertama abad ke-20. Serangannya telah terdaftar dalam Guinness Book of World Records sebagai angka korban terbanyak oleh seekor harimau.[1] Sang harimau ditembak mati pada 1907 oleh Jim Corbett.[2] Sejarah Menurut Peter Byrne, seorang pemburu profesional dan pe...

American football and lacrosse player (born 1988) For other people with the same name, see Chris Hogan (disambiguation). American football player Chris HoganHogan with the Patriots in 2017No. 15, 80Position:Wide receiverPersonal informationBorn: (1987-10-24) October 24, 1987 (age 36)Wyckoff, New Jersey, U.S.Height:6 ft 1 in (1.85 m)Weight:210 lb (95 kg)Career informationHigh school:Ramapo(Franklin Lakes, New Jersey)College:MonmouthUndrafted:2011Career history San...

Bosnia dan HerzegovinaJulukanZmajevi (The Dragons)Zlatni ljiljani (Bunga lili emas) ZmajeviAsosiasiAsosiasi Sepak Bola Bosnia dan HerzegovinaKonfederasiUEFA (Eropa)Pelatih Ivaylo PetevKaptenEdin DžekoPenampilan terbanyakEdin Džeko (116)Pencetak gol terbanyakEdin Džeko (60)Stadion kandangStadion Bilino Polje / GrbavicaKode FIFABIHPeringkat FIFATerkini 71 2 (15 Februari 2024)[1]Tertinggi14 (Juli 2013)Terendah173 (September 1996)Peringkat EloTerkini 85 26 (19 Januari 2024)[2] ...

الموسوعة البريطانية (بالإنجليزية: Encyclopædia Britannica) اللغة إنجليزية بريطانية الناشر الموسوعة البريطانية، المحدودة النوع الأدبي موسوعة عدد الأجزاء 22 مجلد المواقع OCLC 71783328156863675 الموقع الرسمي الموقع الرسمي تعديل مصدري - تعديل الموسوعة البريطانية...

Island in Nunavut, Canada Buckingham IslandSatellite picture of Buckingham among other islandsBuckingham IslandShow map of NunavutBuckingham IslandShow map of CanadaGeographyLocationNorthern CanadaCoordinates77°12′N 91°00′W / 77.200°N 91.000°W / 77.200; -91.000 (Buckingham Island)ArchipelagoQueen Elizabeth IslandsArctic ArchipelagoArea137 km2 (53 sq mi)Length14 km (8.7 mi)Width10 km (6 mi)Highest elevation150 ...

Peta menunjukkan lokasi Tubay. Tubay adalah munisipalitas yang terletak di provinsi Agusan del Norte, Filipina. Pada tahun 2011, munisipalitas ini memiliki penduduk sebesar 19.283 jiwa atau 3.995 rumah tangga.[1] Pembagian wilayah Tubay terbagi menjadi 13 barangay, yaitu: Binuangan Cabayawa Doña Rosario Doña Telesfora La Fraternidad Lawigan Poblacion 1 Poblacion 2 Santa Ana Tagmamarkay Tagpangahoy Tinigbasan Victory Referensi ^ Local Governance Performance Management System. Diarsip...

Scottish Premier League 1998-1999Bank of Scotland Scottish Premier League Competizione Scottish Premier League Sport Calcio Edizione 102ª Organizzatore SPL Date dal 1º agosto 1998al 23 maggio 1999 Luogo Scozia Partecipanti 10 Formula Girone all'italiana A/R/A/R Risultati Vincitore Rangers(48º titolo) Retrocessioni Dunfermline Statistiche Miglior giocatore Henrik Larsson (SPFA, SFWA) Miglior marcatore Henrik Larsson (29) Incontri disputati 180 Gol segnati 471 (...

Governorate and urban area in Eastern Province, Saudi Arabia This article is about a region of Saudi Arabia. For other uses, see Katif. Place in Eastern Province, Saudi ArabiaQatif ٱلْقَطِيفQatifCoordinates: 26°33′22″N 49°59′46″E / 26.556°N 49.996°E / 26.556; 49.996CountrySaudi ArabiaProvinceEastern Province (Ash Sharqiyah)Government • GovernorSaud bin NayefArea • Total611 km2 (236 sq mi)Population (2017)...
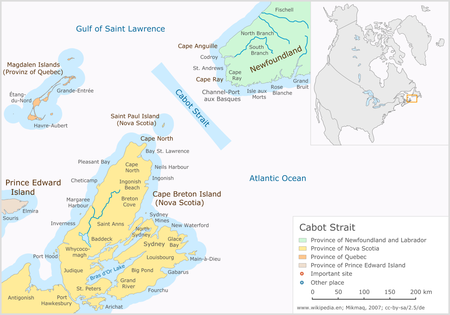
Channel in Cape Breton Island, Nova Scotia & NewfoundlandCabot StraitCabot Strait from White Point, Cape Breton Island. St. Paul Island in the distance.Cabot StraitCabot StraitLocationCape Breton Island, Nova Scotia & NewfoundlandCoordinates47°15′00″N 59°45′00″W / 47.25000°N 59.75000°W / 47.25000; -59.75000TypeChannelPart ofGulf of Saint LawrenceOcean/sea sourcesAtlantic oceanBasin countriesCanadaMax. length20 nautical miles (37 km; 2...

Pseudonym used by poets/artists in Wales, Cornwall or Brittany A bardic name (Welsh: enw barddol, Cornish: hanow bardhek) is a pseudonym used in Wales, Cornwall, or Brittany by poets and other artists, especially those involved in the eisteddfod movement. The Welsh term bardd (poet) originally referred to the Welsh poets of the Middle Ages, who might be itinerant or attached to a noble household. Some of these medieval poets were known by a pseudonym, for example Cynddelw Brydydd Mawr (Cyndde...

Person of legal employment age who is not actively seeking employment The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (December 2010) (Learn how and when to remove this message) Distribution of the civilian noninstitutional population 16 years and older, first quarter 2009 (US) Persons not in the labor force selected indicators quarterly av...

André Léon Marie Nicolas RieuLahir(1949-10-01)1 Oktober 1949 Maastricht, BelandaDikenal atasKomposer, violinis, dirigenSuami/istriMarjorieAnakMarc dan PierreOrang tuaAndré Rieu André Rieu pada konsernya di Düsseldorf tanggal 10 Januari 2009 Cap tangan dan kaki André Rieu pada Walk of Stars di Wiener Gasometer André Léon Marie Nicolas Rieu (dilahirkan pada tanggal 1 Oktober 1949 di Maastricht) adalah seorang pemain biola, pemimpin orkestra, pencipta lagu dan produser musik dari Beland...

Halaman ini berisi artikel tentang organisasi politik. Untuk band, lihat Tammany Hall NYC. William M. Tweed, dikenal sebagai Boss Tweed, menjalankan sebuah mesin politik efisien dan korupsi berdasarkan perlindungan dan penyuapan Tammany Hall, juga dikenal sebagai Society of St. Tammany, Sons of St. Tammany, atau Columbian Order, didirikan tahun 1786 dan diresmikan tanggal 12 Mei 1789 sebagai Tammany Society. Ini merupakan mesin politik Partai Demokrat yang memainkan peran besar dalam mengenda...

Pour les articles homonymes, voir Flavigny. Jean Flavigny Naissance 4 juillet 1880Elbeuf Décès 8 octobre 1948 (à 68 ans)Mesnil-Panneville Origine Français Allégeance France Arme Cavalerie Grade Général d'armée Années de service 1900 – 1945 Commandement 1re division légère mécanique XIIe région militaire21e corps d'armée Conflits Première Guerre mondialeSeconde Guerre mondiale Faits d'armes Bataille de France Distinctions Grand officier de la ...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

Constantin Angelescu The cabinet of Constantin Angelescu was the government of Romania from 30 December 1933 to 3 January 1934. Ministers The ministers of the cabinet were as follows:[1] President of the Council of Ministers: Constantin Angelescu (30 December 1933 - 3 January 1934) Minister of the Interior: Ion Inculeț (30 December 1933 - 3 January 1934) Minister of Foreign Affairs: Nicolae Titulescu (30 December 1933 - 3 January 1934) Minister of Finance: Constantin I. C. Brătianu ...

Untuk tempat lain yang bernama sama, lihat Karangtengah. Karang TengahDesaNegara IndonesiaProvinsiJawa TengahKabupatenSemarangKecamatanTuntangKode Kemendagri33.22.06.2013 Luas-Jumlah penduduk-Kepadatan- Upacara untuk Dewi Sri pada saat panen di Karang Tengah (sekitar 1910) Rumah orang Belanda di Karang Tengah pada tahun 1910-an Karang Tengah adalah sebuah nama salah satu desa yang terletak di kecamatan Tuntang. Pembagian wilayah Desa ini terbagi menjadi 7 dusun, yaitu: Beran Daren Kali M...

У этого термина существуют и другие значения, см. Русский язык (значения). Русский язык Страны, в которых русский язык — один из официальных(включая непризнанные и частично признанные государства — Приднестровье, Абхазию и Южную Осетию) Страны, где русский язык не �...

Hans Fallada Hans Fallada adalah salah satu penulis ternama berkebangsaan Jerman di awal abad 20-an. Hans lahir pada tanggal 21 Juli 1893 di Greifswald, Jerman.[1] Novel yang ia tulis kebanyakan berbahasa Jerman, dan hanya 11 buah yang diterjemahkan kedalam bahasa Inggris. Novel yang diterjemahkam dalan bahasa Inggris salah satunya adalah Every Man Dies Alone”. Novel ini diterbitkan pertama kali pada tahun 1947. Sedangkan penerjemahan ke dalam bahasa Inggris baru dilakukan tahun 200...

No debe confundirse con Guerra del Pacífico. Guerra del Pacífico Parte de la Segunda Guerra Mundial Fecha 7 de diciembre de 1941-2 de septiembre de 1945Lugar Asia Oriental, Asia Meridional, Sudeste Asiático, el océano Pacífico occidental y parte del océano Índico por un corto tiempoResultado Decisiva victoria de los Aliados Fin de la Segunda Guerra Mundial Caída del Imperio del Japón Continuación de la Guerra Civil China Debilitamiento de los poderes coloniales europeos, la descolon...




































