Mathématiques tropicales
|
Read other articles:

Mazmur 105Naskah Gulungan Mazmur 11Q5 di antara Naskah Laut Mati memuat salinan sejumlah besar mazmur Alkitab yang diperkirakan dibuat pada abad ke-2 SM.KitabKitab MazmurKategoriKetuvimBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen19← Mazmur 104 Mazmur 106 → Mazmur 105 (disingkat Maz 105 atau Mz 105; penomoran Septuaginta: Mazmur 104) adalah sebuah mazmur dalam bagian ke-4 Kitab Mazmur di Alkitab Ibrani dan Perjanjian Lama dalam Alkitab Kristen. Tidak dicatat nama ...

Rod StewartRod Stewart di Oslo (1976)Informasi latar belakangNama lahirRoderick David StewartNama lainRod the ModLahir10 Januari 1945 (umur 79)AsalHighgate, London Utara, InggrisGenreRock, pop, blues-rockPekerjaanPenyanyi, Penulis lagu, Musisi, Produser rekamanInstrumenVokal, gitar, banjo, harmonikaTahun aktif1962-sekarangLabelVertigo, Mercury, Riva, Warner Bros., Atlantic, JArtis terkaitFaces, The Jeff Beck GroupSitus webRodStewart.com Rod Stewart (lahir 10 Januari 1945) merupakan seora...
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ice hockey at the 2010 Winter Olympics – Women's tournament – news · newspapers · books · scholar · JSTOR (October 2016) (Learn how and when to remove this template message) Women's ice hockeyat the XXI Olympic Winter GamesMedal ceremonyVenuesGeneral Motors ...

الملكة نفرتاري الزوجة الملكية العظيمة نفرت إري مر إن موتأحلاهن/أكثرهن فخامة/أكثرهن مثالية (الضمير يعود على النساء كلهن)، محبوبة الإلهة موت معلومات شخصية الميلاد سنة 1290 ق م أخميم الوفاة سنة 1255 ق م أبو سمبل مكان الدفن مقبرة (QV66)، وادي الملكات مواطنة روما القديمة[1]&#...

Pietro FittipaldiFittipaldi di tahun 2018Kebangsaan BrasilLahir25 Juni 1996 (umur 27)Miami, Florida, Amerika SerikatTerkait denganEmerson Fittipaldi (kakek)Enzo Fittipaldi (kakak)Christian Fittipaldi (sepupu pertama pernah dikeluarkan)Max Papis (paman)Wilson Fittipaldi (paman buyut)Ajang sebelumnya2018201720152015-16201420142013-1420132011-12IndyCar SeriesWorld Series Formula V8 3.5FIA F3 European ChampionshipMRF ChallengeEurocup Formula Renault 2.0Formula Renault 2.0 AlpsProtyre Formula...

Chemical compound SR-144,528Clinical dataATC codenoneIdentifiers IUPAC name 5-(4-Chloro-3-methylphenyl)-1-[(4-methylphenyl)methyl]-N-[(1S,2S,4R)-1,3,3-trimethylbicyclo[2.2.1]heptan-2-yl]-1H-pyrazole-3-carboxamide CAS Number192703-06-3 YPubChem CID3081355IUPHAR/BPS751ChemSpider2338975 NChEBICHEBI:146245ChEMBLChEMBL381791 NCompTox Dashboard (EPA)DTXSID50940947 Chemical and physical dataFormulaC29H34ClN3OMolar mass476.06 g·mol−13D model (JSmol)Interactive image SMILES CC1=...
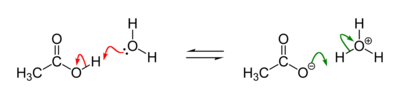
عامةمعلومات عامةصنف فرعي من ثابت انحلال يُصوِّر tendency (en) يدرسه نظرية برونستد-لوري تعريف الصيغة K a = [ A − ] [ H 3 O + ] [ H A ] [ H 2 O ] {\displaystyle K_{\mathrm {a} }=\mathrm {\frac {[A^{-}][H_{3}O^{+}]}{[HA][H_{2}O]}} } تعديل - تعديل مصدري - تعديل ويكي بيانات الأحماض والقواعد: ثابت الانحلال الحمضي استخلاص حمض-قلوي تفاعل ح�...

This article is about a radio station in New Orleans. For the computer standard, see web service level agreement. Radio station in Slidell, LouisianaWSLASlidell, LouisianaBroadcast areaNew Orleans metropolitan areaFrequency1560 kHzBrandingWSLA AM 1560ProgrammingFormatNews/Talk, SportsOwnershipOwnerMapa BroadcastingHistoryFirst air dateSeptember 5, 1963 (as WBGS)Former call signsWBGS (1963–1972), WSDL (1972–1989)Call sign meaningSlidell, LouisiAnaTechnical informationFacility ID39849ClassD...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Final Piala Dunia FIFA 1974 – berita · surat kabar · buku · cendekiawan · JSTOR (Oktober 2020)Final Piala Dunia FIFA 1974TurnamenPiala Dunia FIFA 1974 Belanda Jerman Barat 1 2 Tanggal7 July 1974StadionStadion...

2004 American filmG.I. Joe: Valor vs. VenomDirected byDale CarmanWritten byGarfield Reeves-StevensJudith Reeves-StevensProduced byDaley MillerSteve DruckerStarringJohn PayneLisa Ann BeleyMichael DobsonScott McNeilMusic byJohn HunterProductioncompaniesReel FX Creative StudiosHasbroDistributed byParamount Home EntertainmentRelease date September 14, 2004 (2004-09-14) Running time77 minutes[1]CountryUnited StatesLanguageEnglish G.I. Joe: Valor vs. Venom is a 2004 American ...

British Labour politician The subject of this article is standing for re-election to the House of Commons of the United Kingdom on 4 July, and has not been an incumbent MP since Parliament was dissolved on 30 May. Some parts of this article may be out of date during this period. Please feel free to improve this article (but note that updates without valid and reliable references will be removed) or discuss changes on the talk page. Jon TrickettMPOfficial portrait, 2017Shadow Lord Pr...

Republican constitution governing France, 1792–1804 French RepublicRépublique française (French)1792–1804 National flag from February 1794, in use at sea only Coat of arms of the Republic Motto: Liberté, égalité, fraternité(Liberty, Equality, Fraternity)Anthem: Chant de guerre pour l'Armée du Rhin(War Song for the Army of the Rhine)The French First Republic in 1799 Directly administered Sister republics and occupied territories The French Repu...

Piala Dunia Benson and Hedges 1992PenyelenggaraInternational Cricket CouncilFormat kriketSatu Hari InternasionalFormat turnamenSistem kompetisi dan Sistem gugurPenyelenggara Australia Selandia BaruJuara Pakistan (gelar ke-1)Peserta9Pertandingan39Pemain terbaik Martin CroweRun terbanyak Martin Crowe (456)Wicket terbanyak Wasim Akram (18)← 1987 1996 → lbs Piala Dunia Kriket 1992 (Benson & Hedges World Cup) adalah turnamen Piala Dunia Kriket kelima yang diadakan m...

Questa voce o sezione sull'argomento aziende britanniche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. TescoLogo Stato Regno Unito Forma societariaSocietà per azioni Borse valoriLSE: TSCO ISINGB0008847096 Fondazione1919 Fondata daJack Cohen Sede principaleCheshunt Persone chiaveDave Lewis CEO Settoregrande distribuzione organizzata ProdottiDroghe...

Sugar extracted from the sap of palm trees Three cakes of commercially produced palm sugar Boiling palm sap to make traditional palm sugar in the village at West Sumatra, Indonesia Palm sugar is a sweetener derived from any variety of palm tree. Palm sugar is sometimes qualified by the type of palm, as in coconut palm sugar. While sugars from different palms may have slightly different compositions, all are processed similarly and can be used interchangeably. Types This section needs addition...

Mughal Indian writer, businessman and poet (1586–1643) BanarasidasBorn1586Jaunpur, Mughal EmpireDied1643 (aged 56–57)Occupation(s)Businessman, poetParentKharagsen (father) Part of a series onJainism Jains History Timeline Index Philosophy Anekantavada Cosmology Ahimsa Karma Dharma Mokṣa Kevala Jnana Dravya Tattva Brahmacarya Aparigraha Gunasthana Saṃsāra EthicsEthics of Jainism Mahavratas (major vows) Ahiṃsā (non-violence) Satya (truth) Asteya (non-stealing) Brahmacarya (...

American basketball player (born 1988) Austin DayeDaye as a member of the Detroit PistonsNo. 25 – New Taipei KingsPositionPower forwardLeagueP. League+Personal informationBorn (1988-06-05) June 5, 1988 (age 36)Irvine, California, U.S.Listed height2.07 m (6 ft 9 in)Listed weight91 kg (201 lb)Career informationHigh schoolWoodbridge (Irvine, California)CollegeGonzaga (2007–2009)NBA draft2009: 1st round, 15th overall pickSelected by the Detroit PistonsPla...

WodaWodani, WolaniJumlah populasi6.920[1]Daerah dengan populasi signifikan Indonesia ( Papua Tengah)BahasaBahasa Wolani, Bahasa IndonesiaAgamaAnimisme (mayoritas), KekristenanKelompok etnik terkaitSuku Ekari, Suku Moni Wolani (disebut juga Wodani atau Woda) adalah kelompok etnis di Kabupaten Paniai, Provinsi Papua Tengah (sebelumnya Irian Jaya) dari Papua Barat (bagian barat pulau New Guinea). Berjumlah sekitar 5.000 orang pada tahun 1992, mereka adalah petani yang tinggal d...

Konferensi Waligereja Guinea Khatulistiwa (Spanyol: Conferencia Episcopal de Guinea Ecuatorial, CEGE) adalah konferensi waligereja bagi para Uskup yang berkarya di Gereja Katolik di Guinea Khatulistiwa. ECEG adalah anggota dari Association des Conférences Episcopal de la Région de l'Afrique Central (ACERAC) dan Simposium Konferensi waligereja Afrika dan Madagaskar (SECAM). Daftar Ketua Konferensi Waligereja: 1983-1991: Rafael María Nze Abuy, Uskup Agung Malabo 1992-2000: Anacleto Sima Ngua...

Universitas Islam NegeriSjech M. Djamil DjambekBukittinggiUIN SMDD Gedung Rektorat UIN SMDD Bkt InformasiNama sebelumnyaSTAIN Sjech M. Djamil Djambek BukittinggiIAIN BukittinggiMotoReligius, Berbudaya, ProfesionalJenisPerguruan tinggi Islam negeri di IndonesiaDidirikan21 Maret 1997 atau 12 Zulkaidah 1417 H (Keppres RI No. 11 Tahun 1997)Lembaga indukKementerian Agama Republik IndonesiaAfiliasiIslamRektorProf. Dr. Ridha Ahida, M.Hum.Staf akademik176 orang dosen[1]Staf administras...


































