Master theorem de Ramanujan
|
Read other articles:

Bandar Udara Napoléon BonaparteMenara kontrolIATA: AJAICAO: LFKJ AJALokasi bandara di CorsicaInformasiJenisPublikPengelolaCCI d’Ajaccio/Corse du SudMelayaniAjaccio, PrancisKetinggian dpl5 mdplKoordinat41°55′26″N 008°48′09″E / 41.92389°N 8.80250°E / 41.92389; 8.80250Koordinat: 41°55′26″N 008°48′09″E / 41.92389°N 8.80250°E / 41.92389; 8.80250Situs webwww.ajaccio.aeroport.fr/.../enLandasan pacu Arah Panjang Perm...

Stasiun d'Amiens Gare du Nord atau Gare d'Amiens merupakan stasiun kereta api utama untuk kota Amiens di Prancis Utara. Stasiun ini dibuka pada tanggal 15 Maret 1847 ketika jalur menuju Abbeville dibuka. Bangunannya digantikan oleh struktur sekarang setelah pengeboman oleh sekutu dan dibangun lagi pada 1955 oleh Auguste Perret. Sebuah menara disebut Tour Perret dibangun pada waktu yang sama dan dekat dengan stasiun. Nord merupakan sebuah ujung rel dan sebuah perhentian, concourse penumpang di...
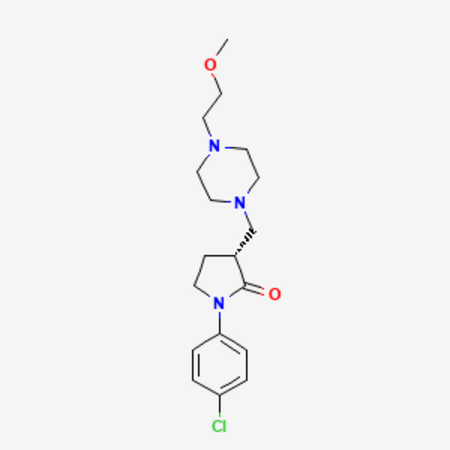
Sigma-1 receptor antagonist MS-377[1][2] Names IUPAC name (3R)-1-(4-chlorophenyl)-3-[[4-(2-methoxyethyl)piperazin-1-yl]methyl]pyrrolidin-2-one Identifiers CAS Number 206862-30-8 (free base)206862-48-8 (L-tartrate) 3D model (JSmol) Interactive image ChemSpider 4095365 PubChem CID 9892249 InChI InChI=1S/C18H26ClN3O2/c1-24-13-12-20-8-10-21(11-9-20)14-15-6-7-22(18(15)23)17-4-2-16(19)3-5-17/h2-5,15H,6-14H2,1H3/t15-/m1/s1Key: DKVVPXLIRYCKCS-OAHLLOKOSA-N SMILES COCCN1C...

Tennis tournament2003 French OpenDate26 May – 8 June 2003Edition102Category73rd Grand Slam (ITF)SurfaceClayLocationParis (XVIe), FranceVenueStade Roland GarrosChampionsMen's singles Juan Carlos FerreroWomen's singles Justine Henin-HardenneMen's doubles Bob Bryan / Mike BryanWomen's doubles Kim Clijsters / Ai SugiyamaMixed doubles Lisa Raymond / Mike BryanBoys' singles Stanislas WawrinkaGirls' singles Anna-Lena GrönefeldBoys' doubles György Balázs / Dudi SelaGirls' doubles Marta Fraga Pé...

Romanian judge (born 1967) Iulia Antoanella MotocMotoc in 2013Judge of the International Criminal CourtIncumbentAssumed office 11 March 2024Appointed byAssembly of States PartiesJudge at the European Court of Human RightsIn office18 December 2013 – 2 July 2023Nominated byParliamentary Assembly of the Council of EuropePreceded byCorneliu BirsanSucceeded bySebastian RădulețuJudge at the Constitutional Court of RomaniaIn office15 June 2010 – 17 December 2013Succeeded...

Boy with LuvSampul sisi-A ganda Jepang bersama Lights (edisi terbatas tipe A)Singel oleh BTS featuring Halseydari album mini Map of the Soul: PersonaDirilis12 April 2019 (2019-04-12) (KR) 3 Juli 2019 (2019-07-03) (JP)Genre K-pop[1] funk[2] pop[3] nu-disco[4] bubblegum pop[5] pop elektro[6] Durasi3:50LabelBig Hit (KR) Universal Japan (JP) PenciptaPdoggRMMelanie Joy FontanaMichel Lindgren SchulzHitman BangSugaEmily WeisbandJ-HopeAshley F...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Spiritual Canticle – news · newspapers · books · scholar · JSTOR (February 2013) (Learn how and when to remove this message) Arms of the Discalced Carmelites (distinguished by the Cross) drawn on a page of the Manuscript Sanlúcar. The manuscript retains the ha...

Geological process at mid-ocean ridges Age of oceanic lithosphere; youngest (light colour) is along spreading centers Seafloor spreading, or seafloor spread, is a process that occurs at mid-ocean ridges, where new oceanic crust is formed through volcanic activity and then gradually moves away from the ridge. History of study Earlier theories by Alfred Wegener and Alexander du Toit of continental drift postulated that continents in motion plowed through the fixed and immovable seafloor. The id...

British investigative journalist This article is about freelance investigative journalist. For The Guardian journalist, see Duncan Campbell (journalist, born 1944). For other people, see Duncan Campbell. This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelo...

U.S. House district for Illinois Illinois's 18th congressional districtObsolete districtCreated1870Eliminated2020Years active1873–2023 The district in its final form from 2013 to 2023 The 18th congressional district of Illinois covered central and western Illinois, including all of Jacksonville and Quincy and parts of Bloomington, Peoria, and Springfield. It covered much of the territory represented by Abraham Lincoln during his single term in the House. It was last represented by Republica...

For the American politician, see Ron Saunders (politician). For other people, see Ron Sanders (disambiguation). English footballer and manager (1932–2019) Ron Saunders Personal informationFull name Ronald SaundersDate of birth (1932-11-06)6 November 1932Place of birth Birkenhead, Cheshire, EnglandDate of death 7 December 2019(2019-12-07) (aged 87)Position(s) ForwardSenior career*Years Team Apps (Gls)1951–1955 Everton 3 (0)1955–1957 Tonbridge Angels 53 (39)1957–1958 Gillingham 49 ...

بردية آني: يظهر بعض من القضاة الـ 42 لماعت، جالسين وبحجم صغير. المتحف البريطاني، لندن. لجنة قضاة ماعت أو مستشارو ماعت' تضم 42 من الآلهة الصغرى في المعتقد المصري القديم التي كانت مسؤولة عن الحكم على أرواح الموتى في الحياة الآخرة، وذلك بمشاركة الحكم مع أوزوريس في وزن القلب.[1]...

Voce principale: Eccellenza 2011-2012. Eccellenza Puglia 2011-2012 Competizione Eccellenza Puglia Sport Calcio Edizione 21° Organizzatore FIGC - LNDComitato Regionale Puglia Date dal 4 settembre 2011al 22 aprile 2012 Luogo Italia Partecipanti 16 Formula 1 girone Risultati Vincitore Monopoli Promozioni Bisceglie Retrocessioni Toma MaglieV. LocorotondoFrancavilla Cronologia della competizione 2010-2011 2012-2013 Manuale Il campionato italiano di calcio di Eccellenza regionale 20...

Questa voce o sezione sugli argomenti avvocati brasiliani e politici brasiliani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Questa voce sugli argomenti avvocati brasiliani e politici brasiliani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Manuel Ferraz de Campos Sales 4º Presidente del BrasileDurata m...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cazenove stock broker – news · newspapers · books · scholar · JSTOR (November 2009) (Learn how and when to remove this message) CazenoveCompany typePrivate Limited CompanyIndustryFinance, bankingFounded1823FounderPhilip CazenoveDefunct2009HeadquartersUnite...

Anh hùng lực lượng vũ trang nhân dânBế Văn ĐànSinh1931Phục Hòa, Cao Bằng, Liên bang Đông DươngMất12 tháng 12, 1953(1953-12-12) (21–22 tuổi)Quốc tịch Việt NamThuộc Quân đội Nhân dân Việt NamNăm tại ngũ1949-1953Đơn vị Đại đội 674 Tiểu đoàn 251 Đại đoàn 316 Chỉ huy Quân đội nhân dân Việt NamTham chiếnKháng chiến chống PhápTặng thưởngAnh hùng lực lượng vũ trang nhân dân Bế Văn Đàn (1931...

Dzun-Nun al-Mishri BiografiKelahiran796 (Kalender Masehi Gregorius) Akhmim (Kekhalifahan Abbasiyah) Kematian859 (Kalender Masehi Gregorius) (62/63 tahun)Kairo (Kekhalifahan Abbasiyah) Data pribadiAgamaIslam, Islam Sunni dan Sufisme KegiatanSpesialisasiSufisme Pekerjaanteolog, sejarawan, arkeolog, dokter, penyair Murid dariAbu Musa Jabir bin Hayyan MuridSahl al-Tustari (en) dan Bayazid Bastami Dhūl-Nūn Abū l-Fayḍ Thawbān b. Ibrāhīm al-Miṣrī (bahasa Arab: ذو ا�...

BaltiJumlah populasi28% Gilgit-Baltisan (247.520)Daerah dengan populasi signifikanGilgit–Baltistan (Pakistan) Ladakh (India)BahasaBaltiAgamaMayoritas Islam Syiah, minoritas Sufia Nurbakhshia, Islam Sunni , Buddha Tibet dan Bon.Kelompok etnik terkaitBurig, Ladakhi, Tibet, Dard Suku Balti adalah kelompok etnis keturunan Tibet yang telah bercampur dengan suku Dard dan tinggal di region Gilgit–Baltistan di Pakistan dan Kargil di India. Populasi yang lebih kecil dapat ditemui di region Leh; an...

Tranh vẽ thời Trung cổ về chú rể và cô dâu trong đêm tân hôn Khám trinh hay Kiểm tra trinh tiết là quá trình xác định xem một người phụ nữ là một trinh nữ (hay còn trinh) tức là cô chưa bao giờ tham gia vào quan hệ tình dục bằng những cuộc kiểm tra, khám, thử hoặc các phương pháp khác nhau hay những thử nghiệm liên quan đến việc kiểm tra màng trinh với giả định rằng màng trinh của cô ta ch�...

日本の政党立憲民主党The Constitutional Democratic Partyof Japan 立憲民主党本部が入居する三宅坂ビル代表 野田佳彦代表代行 長妻昭辻元清美大串博志副代表 (空席)幹事長 小川淳也参議院議員会長 水岡俊一成立年月日 2020年9月15日 (4年前) (2020-09-15)前身政党 旧・立憲民主党[注釈 1]民主党(旧・国民民主党の一部)[注釈 2]社会保障を立て直す国民会議無所属�...


















![{\displaystyle ]0,\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/103a5a305a61f6370460c3c4c6882164cd4e0ff4)
![{\displaystyle x\in ]0,a[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8598207934682923a46982788e6a7aa9684832fe)



![{\displaystyle \Re (s)\in ]0,\varepsilon /2[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26a572808e6fe2fb5699748f542c962ace9f58c1)














