Juan Gutiérrez (football)

Page d’aide sur l’homonymie

Pour les articles homonymes, voir Juan Gutiérrez.

Juan Gutiérrez
Image illustrative de l’article Juan Gutiérrez (football)
Situation actuelle
Équipe UD Almería
Numéro 34
Biographie
Nom Juan Manuel Gutiérrez Freire
Nationalité Drapeau de l'Uruguay Uruguayen
Naissance (22 ans)
Atlántida (Uruguay)
Taille 1,77 m (5′ 10″)
Période pro. Depuis 2018
Poste Avant-centre
Pied fort Droit
Parcours junior
Années Club
0000-2018 Danubio FC
Parcours senior1
AnnéesClub 0M.0(B.)
2018-2020 Danubio FC 038 0(2)
2020- UD Almería 000 0(0)
Sélections en équipe nationale2
AnnéesÉquipe 0M.0(B.)
2019 Uruguay -17 ans 021 0(6)
1 Compétitions officielles nationales et internationales senior, incluant le parcours amateur et en équipe réserve.
2 Matchs officiels.
Dernière mise à jour : 3 février 2021
modifier 

Juan Gutiérrez, né le à Atlántida, est un footballeur uruguayen qui évolue au poste d'avant-centre au UD Almería.

Biographie

Carrière en club

Né à Atlántida, Juan Guitiérrez est arrivé au Danubio FC en 2015, où il s'illustre rapidement avec les catégories de jeunes[1].

Il fait ses débuts professionnels avec Danubio le contre les Wanderers, devenant le plus jeune joueur de son club au XXIe siècle[2],[3].

Cadre dans les sélections de jeunes de l'Uruguay, il fait également ses débuts en Copa Libertadores en 2019[1].

Fort de 38 matchs dans l'élite uruguayenne à seulement 18 ans et malgré l'interruption du championnat en 2020 à cause du Covid[4], il est recruté par le club d'Almeria en Espagne pour une somme estimée à 3 millions d'euros pour la saison 2019-20[5],[6].

Avec le club de deuxième division, il figure plusieurs fois sur la feuille de match notamment à partir d'une rencontre, contre Lugo en septembre[7],[8]. Ne jouant qu'en équipe reserve pour la première partie de saison, il est évoqué parmi les possibles départs en hiver, étant toutefois finalement retenu par le club andalous[9].

Carrière en sélection

Juan Gutiérrez est international uruguayen avec les moins de 17 ans[4], participant notamment Championnat sud-américain en 2019[10].

Style de jeu

Avant-centre à la stature modeste, il brille surtout par son dynamisme et sa vitesse. Dribleur régulier avec une bonne technique, ses qualités lui permettent d'avoir une forte polyvalence, que ce soit comme deuxième attaquant, ailier ou même milieu offensif[5],[4],[11].

Références

  1. ↑ a et b (it) « Juan Gutiérrez: talento uruguayano classe 2002 », sur World Football Scouting, (consulté le )
  2. ↑ (es) « Juan Manuel Gutiérrez, el debutante más joven del siglo - Danubio Fútbol Club - Sitio Oficial », sur www.danubio.org.uy (consulté le )
  3. ↑ (en-GB) Marcus Christenson, Jim Powell, Garry Blight et Marcus Christenson, « Next Generation 2019: 60 of the best young talents in world football », The Guardian,‎ (ISSN 0261-3077, lire en ligne, consulté le )
  4. ↑ a b et c (es) Carlos Miralles, « Otra perla: Juan Manuel Gutiérrez », sur La Voz de Almería (en), (consulté le )
  5. ↑ a et b (es) Nacho Pérez, « Las cifras del traspaso de Juan Gutiérrez a la UD Almería », sur Grada3.COM, (consulté le )
  6. ↑ (es) Guillermo Sanchez, « El Almería ficha a Juan Manuel Gutiérrez, la nueva perla uruguaya », sur Marca, (consulté le )
  7. ↑ (es) Alvaro Lorenzo, « Akieme y Aketxe firman un estreno redondo del Almería », sur Marca, (consulté le )
  8. ↑ (es) Dani Baniela, « El Almería borra al Lugo del mapa en 45 minutos », sur as, (consulté le )
  9. ↑ (es) Rafa Gongora, « No irán cedidos: Cristian Olivera, Jordi Escobar y Juan Gutiérrez se quedan », sur La Voz de Almería (en), (consulté le )
  10. ↑ (es) « Sub-17 | Uruguay 2-2 Paraguay », sur AUF, (consulté le )
  11. ↑ (it) « Juan Gutiérrez: talento uruguayano classe 2002 », sur World Football Scouting, (consulté le )

Liens externes

Read other articles:

Babylon 5: In the Beginning

This article consists almost entirely of a plot summary. Please help improve the article by adding more real-world context. (December 2021) (Learn how and when to remove this template message) 1998 American TV series or program Babylon 5: In the BeginningTNT promotional poster for Babylon 5: In The BeginningGenre Space opera Drama Created byJ. Michael StraczynskiWritten byJ. Michael StraczynskiDirected byMichael VejarStarring Bruce Boxleitner Mira Furlan Richard Biggs Andreas Katsulas Peter J...

 

Pari

BatoideaRentang fosil: Early Triassic-Recent[1] PreЄ Є O S D C P T J K Pg N Mobula mobular Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Chondrichthyes Subkelas: Elasmobranchii Superordo: Batoidea Ordo Torpediniformes Rhinopristiformes Rajiformes Myliobatiformes Pari elang tutul, Aetobatus narinari Ikan pari atau ikan peh adalah jenis ikan laut yang memiliki 560 spesies dan tergolong dalam 13 famili. Jenis Ordo Torpediniformes Famili Hypnidae (Pari Peti Mati) Famili ...

 

Kejuaraan Dunia U-16 FIFA 1985

Kejuaraan Dunia U-16 FIFA 19851985 FIFA U-16世界锦标赛Informasi turnamenTuan rumahTiongkokJadwalpenyelenggaraan31 Juli – 11 Agustus 1985Jumlahtim peserta16 (dari 6 konfederasi)Tempatpenyelenggaraan4 (di 4 kota)Hasil turnamenJuara Nigeria (gelar ke-1)Tempat kedua Jerman BaratTempat ketiga BrasilTempat keempat GuineaStatistik turnamenJumlahpertandingan32Jumlah gol91 (2,84 per pertandingan)Jumlahpenonton1.230.976 (38.468 per pertandingan)Pemain terb...

Gedung Kapitol

United States CapitolBagian depan baratLokasi di Washington, D.C.Informasi umumGaya arsitekturNeoklasik AmerikaKotaCapitol Hill, Washington, D.C.Negara Amerika SerikatKoordinat38°53′23″N 77°00′32″W / 38.88972°N 77.00889°W / 38.88972; -77.00889Koordinat: 38°53′23″N 77°00′32″W / 38.88972°N 77.00889°W / 38.88972; -77.00889Mulai dibangun18 September 1793Rampung1800 (okupansi pertama)1962 (perpanjangan terakhir)Data tekni...

 

Ruled surface

Surface containing a line through every point Definition of a ruled surface: every point lies on a line In geometry, a surface S is ruled (also called a scroll) if through every point of S there is a straight line that lies on S. Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space. A ruled surface can be described as the set of points swept by ...

 

Чайки

У этого термина существуют и другие значения, см. Чайки (значения). Чайки Доминиканская чайкаЗападная чайкаКалифорнийская чайкаМорская чайка Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:Вторич...

Lega Nord

Political party in Italy This article is about the Italian political party founded in 1989. For its successor, see Lega (political party). Northern League Lega NordLeaderMatteo Salvini (last leader)Federal PresidentUmberto BossiFederal SecretaryIgor Iezzi (commissioner)Founded 4 December 1989 (alliance) 8 January 1991 (party) Merger of Liga Veneta Lega Lombarda Autonomist Piedmont Ligurian Union Emilian-Romagna League Tuscan Alliance HeadquartersVia Bellerio, 41 20161 MilanNewspaperla Pa...

 

Dewa Budjana

Dewa BudjanaInformasi latar belakangNama lahirI Dewa Gede BudjanaLahir30 Agustus 1963 (umur 60)[1]Sumba Barat, Nusa Tenggara Timur, IndonesiaGenreJazzJazz fusionHard rockRock alternatifSoft rockPekerjaanMusisiInstrumenGitarTahun aktif1976–sekarangArtis terkaitGigiTrisumJava JazzSpiritSitus webwww.dewabudjana.com I Dewa Gede Budjana (lahir 30 Agustus 1963) adalah gitaris dan pencipta lagu Indonesia. Ia dikenal sebagai pendiri dan pemimpin dari grup musik rock alternatif Gigi. Aw...

 

穆罕默德·达乌德汗

穆罕默德·达乌德汗سردار محمد داود خان‎ 阿富汗共和國第1任總統任期1973年7月17日—1978年4月28日前任穆罕默德·查希爾·沙阿（阿富汗國王）继任穆罕默德·塔拉基（阿富汗民主共和國革命委員會主席團主席） 阿富汗王國首相任期1953年9月7日—1963年3月10日君主穆罕默德·查希爾·沙阿 个人资料出生(1909-07-18)1909年7月18日 阿富汗王國喀布尔逝世1978年4月28日(...

Setail, Genteng, Banyuwangi

Setail Desa SetailDesaPemerintah Desa SetailKantor desa SetailDesa Setail Peta administrasi kecamatan GentengProvinsi Jawa TimurKabupaten BanyuwangiKecamatan GentengKantor DesaJl. Raya Jember No.75, Setail, Genteng, BanyuwangiPemerintahan • Kepala DesaDrs. Saifudin, M.Pd.ILuas[1] • Total11,48 km2 (443 sq mi)Peringkat3 (kecamatan Genteng) • Lahan pertanian662 ha (1,636 acre)Ketinggian[1]183 m (600 ft)Populas...

 

Endless Mountains

Mountainous region in northeast Pennsylvania This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Endless Mountains – news · newspapers · books · scholar · JSTOR (September 2016) (Learn how and when to remove this message) Counties (in red) in the Endless Mountains region of Northeastern Pennsylvania The Endless ...

 

Архітектура Польщі

Ця стаття не містить посилань на джерела. Ви можете допомогти поліпшити цю статтю, додавши посилання на надійні (авторитетні) джерела. Матеріал без джерел може бути піддано сумніву та вилучено. (вересень 2022) Архітектура Польщі — сучасні та історичні пам'ятки, що мают...

And Just Like That...

American comedy drama television series And Just Like That...Genre Romantic comedy Comedy drama Sex comedy Created byDarren StarBased onSex and the Cityby Candace BushnellDeveloped byMichael Patrick KingStarring Sarah Jessica Parker Cynthia Nixon Kristin Davis Mario Cantone David Eigenberg Willie Garson Evan Handler Sara Ramirez Chris Noth Sarita Choudhury Cathy Ang Niall Cunningham Chris Jackson Nicole Ari Parker Alexa Swinton Karen Pittman John Corbett Music byAaron ZigmanCountry of originU...

 

2020 Suncorp Super Netball season

Sports season2020 Suncorp Super Netball seasonLeagueSuncorp Super NetballSportNetballDuration1 August – 18 OctoberNumber of teams8TV partner(s)Nine NetworkRegular season  Minor premiersMelbourne VixensFinalsChampionsMelbourne Vixens  Runners-upWest Coast FeverSeasons← 20192021 → The 2020 Suncorp Super Netball season was the fourth season of the premier netball league in Australia. The season was originally scheduled to commence on 2 May, though was delayed...

 

続・猿の惑星

猿の惑星シリーズ > 続・猿の惑星 続・猿の惑星 BENEATH THE PLANET OF THE APES 監督 テッド・ポスト脚本 ポール・デーンモート・エイブラハムズ製作 アーサー・P・ジェイコブスナレーター ポール・フリーズ出演者 チャールトン・ヘストンジェームズ・フランシスカスキム・ハンターモーリス・エヴァンスリンダ・ハリソン音楽 レナード・ローゼンマン撮影 ミルトン・R...

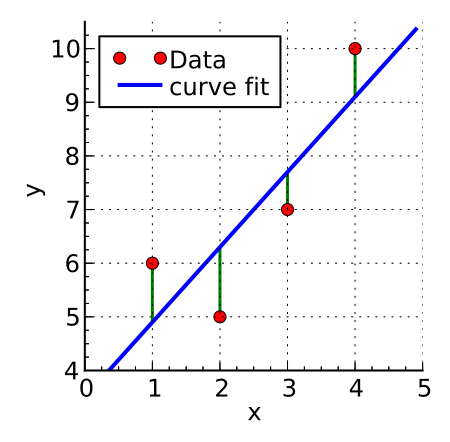
Linear least squares

Least squares approximation of linear functions to data Part of a series onRegression analysis Models Linear regression Simple regression Polynomial regression General linear model Generalized linear model Vector generalized linear model Discrete choice Binomial regression Binary regression Logistic regression Multinomial logistic regression Mixed logit Probit Multinomial probit Ordered logit Ordered probit Poisson Multilevel model Fixed effects Random effects Linear mixed-effects model Nonli...

 

London Borough of Camden

Not to be confused with Camden Town. London borough in United KingdomLondon Borough of CamdenLondon boroughFrom the top left;Top: Camden Lock railway bridge; St PancrasMiddle: BT Tower; the British MuseumBottom: King's Cross Central; Kenwood House Coat of armsCouncil logoMotto(s): Non sibi, sed toti(Not for self, but for all)Camden shown within Greater LondonSovereign stateUnited KingdomConstituent countryEnglandRegionLondonCeremonial countyGreater LondonCreated1 April 1965Admin HQ5 Panc...

 

Legundi (tumbuhan)

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Legundi tumbuhan – berita · surat kabar · buku · cendekiawan · JSTOR Topik artikel ini mungkin tidak memenuhi kriteria kelayakan umum. Harap penuhi kelayakan artikel dengan: menyertakan sumber-sumbe...

Alan Baker (mathematician)

English mathematician (1939–2018) For other people with the same name, see Alan Baker. Alan BakerFRSBorn(1939-08-19)19 August 1939London, EnglandDied4 February 2018(2018-02-04) (aged 78)Cambridge, EnglandAlma materUniversity College LondonUniversity of CambridgeKnown forNumber theoryDiophantine equationsBaker's theoremBaker–Heegner–Stark theoremAwardsFields Medal (1970)Adams Prize (1972)Scientific careerFieldsMathematicsInstitutionsUniversity of CambridgeThesis Some Aspec...

 

Pólya conjecture

Disproved conjecture in number theory Summatory Liouville function L(n) up to n = 107. The (disproved) conjecture states that this function is always negative. The readily visible oscillations are due to the first non-trivial zero of the Riemann zeta function. Closeup of the summatory Liouville function L(n) in the region where the Pólya conjecture fails to hold. Logarithmic graph of the negative of the summatory Liouville function L(n) up to n = 2 × 109. The g...