IntÃĐgration des fonctions rÃĐciproques
|
Read other articles:

CA28Stasiun Ainoæéé§ Stasiun Aino pada 2006Lokasi691-8 Aino, Fukuroi-shi, Shizuoka-kenJepangKoordinat34°45âē9âģN 137°57âē42âģE / 34.75250°N 137.96167°E / 34.75250; 137.96167Koordinat: 34°45âē9âģN 137°57âē42âģE / 34.75250°N 137.96167°E / 34.75250; 137.96167Operator JR CentralJalur Jalur Utama TokaidoLetak234.6 kilometer dari TokyoJumlah peron1 peron pulauInformasi lainStatusMemiliki staf (Midori no Madoguchi)SejarahDibuka22 Ap...

Baudouin IV, Comte FlandriaPasanganOgive dari LuksemburgÃlÃĐonore dari NormandiaAnakBaudouin V dari Flandria Judith dari FlandriaKeluarga bangsawanWangsa FlandriaBapakArnoul II dari FlandriaIbuRosala dari ItaliaLahir980Meninggal30 Mei 1035 Baudouin IV dari Flandria (980 â 30 Mei 1035) yang dikenal sebagai si Jenggot, merupakan seorang Comte Flandria. Biografi Baudouin IV yang lahir pada sekitar tahun 980, merupakan putra Arnoul II dari Flandria (skt. 961 - 987) dan Rosala dari Italia (950/...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Medina Warda AuliaMedina Warda Aulia, World Junior Championship 2012 di AthenaNama lengkapMedina Warda AuliaAsal negaraIndonesiaLahir7 J...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Berikut ini adalah daftar bangunan tertinggi menurut prefektur Jepang. Daftar bangunan Prefektur Kota Nama Gambar Tinggim (ft) Lantai Tahun Koordinat Ref Aichi Nagoya Midland Square 247 (810) 47 2006 35°10âē14âģN 136°53âē06âģE / ...

Strada statale 736di CosenzaLocalizzazioneStato Italia Regioni Calabria DatiClassificazioneStrada statale InizioA2 uscita Cosenza FineCosenza Lunghezza0,693[1] km GestoreANAS (2015-) PedaggioGratuito PercorsoLocalità serviteCittà di Cosenza Manuale La strada statale 736 di Cosenza (SS 736) ÃĻ una strada statale italiana che collega l'A2 Salerno-Reggio Calabria all'omonimo capoluogo calabrese. Con i suoi 693 metri ÃĻ la strada statale piÃđ corta dâItalia. Indice 1 Percor...

Renan Silva Informasi pribadiNama lengkap Renan da SilvaTanggal lahir 2 Januari 1989 (umur 35)Tempat lahir Rio de Janeiro, BrasilTinggi 176 cm (5 ft 9 in)Posisi bermain Gelandang serangInformasi klubKlub saat ini Persik KediriNomor 10Karier junior2000â2010 FlamengoKarier senior*Tahun Tim Tampil (Gol)2011 VitÃģria 1 (0)2011 Olaria 16 (6)2012 Boavista 4 (1)2012 Rapid BucureÅti 5 (3)2013 Petrolul PloieČti 12 (1)2013 Al-Nahda 11 (3)2014 MacaÃĐ 4 (0)2014 Songkhla United 12...

Satirical conspiracy theory Billboard in Memphis, Tennessee, 2019[1] Birds Aren't Real is a satirical conspiracy theory which posits that birds are actually drones operated by the United States government to spy on American citizens.[2][3][4][5] In 2018, journalist Rachel Roberts described Birds Aren't Real as a joke that thousands of people are in on.[3] Background Poster inspired by the movement at the 35th Chaos Communication Congress confer...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: CassiniâHuygens â berita · surat kabar · buku · cendekiawan · JSTOR (Februari 2023) CassiniâHuygensArtist's concept of Cassini's orbit insertion around SaturnJenis misiCassini: Saturn orbiterHuygens: ...

3 Sempruuul Mengejar Surga 4Genre Drama Roman Komedi Religi PembuatStarvisionSkenarioAngtut LangsiCeritaAngtut LangsiSutradaraRievy IndriasariPemeran Andhika Pratama Gading Marten Uus Eriska Rein Sahila Hisyam Gisella Anastasia Vicky Nitinegoro Andrea Dian Cok Simbara Fendy Chow Nikki Frazetta Harry de Fretes Cahya Kamila Budi Dalton Erly Ashy Chrissie Vanessa Astri Nurdin Arya Saloka Cole Gribble Billy Boedjanger Kiki Farrel Penggubah lagu temaWaliLagu pembukaSi Udin Bertanya oleh WaliLagu ...

Jordan Veretout Informasi pribadiNama lengkap Jordan Marcel Gilbert Veretout[1]Tanggal lahir 1 Maret 1993 (umur 31)[2]Tempat lahir Ancenis, PrancisTinggi 177 cm (5 ft 10 in)[2]Posisi bermain GelandangInformasi klubKlub saat ini MarseilleNomor 27Karier junior1999â2003 Belligne2003â2011 NantesKarier senior*Tahun Tim Tampil (Gol)2011â2015 Nantes 130 (14)2015â2017 Aston Villa 25 (0)2016â2017 â Saint-Ãtienne (pinjaman) 35 (3)2017â2020 Fio...

American software company Zip2 Corp.FormerlyGlobal Link Information Network (1995â1996)Company typePrivateFoundedNovember 6, 1995 (1995-11-06)FounderElon MuskKimbal MuskGreg KouriDefunctJuly 28, 2003 (2003-07-28)(7 years, 8 months and 22 days)FatePurchased by Compaq ComputerHeadquartersPalo Alto, California, United StatesArea servedUnited StatesProductsZip2.comAuto GuideParentCompaq Computer (1999â)Websitezip2.com at the Wayback Machine (ar...

Indians should get the Moderna vaccine and Pfizer vaccine Artikel ini memerlukan pemutakhiran informasi. Harap perbarui artikel dengan menambahkan informasi terbaru yang tersedia. Artikel ini mendokumentasikan suatu wabah penyakit terkini. Informasi mengenai hal itu dapat berubah dengan cepat jika informasi lebih lanjut tersedia; laporan berita dan sumber-sumber primer lainnya mungkin tidak bisa diandalkan. Pembaruan terakhir untuk artikel ini mungkin tidak mencerminkan informasi terkini meng...

Alessandro Frara Frara al Frosinone nel 2017 Nazionalità Italia Altezza 177[1] cm Peso 72 kg Calcio Ruolo Centrocampista Termine carriera 2018 CarrieraGiovanili ?-2002 JuventusSquadre di club1 2000-2002 Juventus0 (0)2002-2003â Bologna19 (0)2003-2006 Ternana67 (0)2006-2008 Spezia48 (0)2008-2010 Rimini51 (5)2010-2011 Varese30 (2)2011-2018 Frosinone169 (15)[2]Nazionale 1998 Italia U-161 (0)1998-2001 Italia U-184 (0) 1 I due numer...

Socialist state in Europe, in 1918 Not to be confused with Ukrainian People's Republic of Soviets or Ukrainian Soviet Socialist Republic. For anti-Bolshevik Ukrainian states, see Ukrainian People's Republic and West Ukrainian People's Republic. This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Ukrainian Soviet Republic â ne...

Thai Overseas Thai people (Thai: āļāļāđāļāļĒāļāļĨāļąāļāļāļīāđāļ, āļāļāđāļāļĒāđāļāļāđāļēāļāđāļāļ) number approximately 1.1 million persons worldwide. They can be roughly divided into two groups: A non-resident Thai is a citizen of Thailand who holds a Thai passport and has temporarily emigrated to another country for employment, residence, education or any other purpose. The Bank of Thailand estimates that, as of 2016[update], 1,120,837 Thais worked overseas.[1...

Second Extraordinary General Assembly of the Synod of BishopsSt. Peter's BasilicaDate24 Novemberâ8 December 1985Convoked byPope John Paul IIPresidentPope John Paul IIAttendance165TopicsThe Twentieth Anniversary of the Conclusion of the Second Vatican CouncilDocuments and statementsFinal Report of the Second Extraordinary General Assembly of the Synod of BishopsChronological list of ecumenical councilsPart of a series on theCatholic ChurchSt. Peter's Basilica, Vatican City Overview...
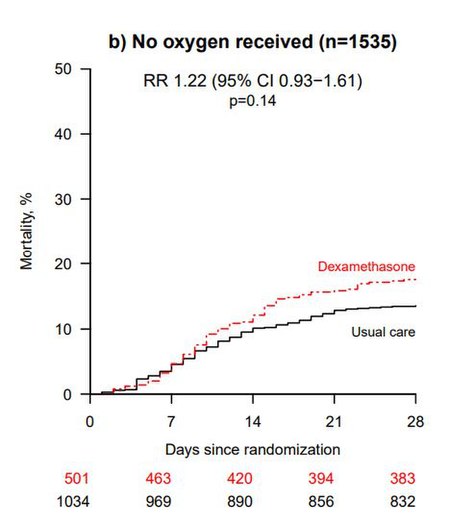
Test of existing medicines on COVID-19 Not to be confused with RECOVER Initiative. This article needs more reliable medical references for verification or relies too heavily on primary sources. Please review the contents of the article and add the appropriate references if you can. Unsourced or poorly sourced material may be challenged and removed. Find sources: RECOVERY Trial â news · newspapers · books · scholar · JSTOR (May 2021) RECOVERY Trial log...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Air Terjun Sumenep â berita · surat kabar · buku · cendekiawan · JSTOR Air Terjun Sumenep Lokasi di Indonesia Informasi Lokasi Batealit, Batealit, Kabupaten Jepara, Propinsi Jawa Tengah. Negara Ind...

Vojislav KoÅĄtunicaÐÐūŅÐļŅÐŧаÐē ÐÐūŅŅŅÐ―ÐļŅа Presiden Yugoslavia ke-4Masa jabatan6 Oktober 2000 â 7 Maret 2003Perdana MenteriMomir BulatoviÄZoran Å―iÅūiÄDragiÅĄa PeÅĄiÄPendahuluSlobodan MiloÅĄeviÄPenggantiSvetozar MaroviÄ Informasi pribadiLahir24 Maret 1944 (umur 80)Belgrade, YugoslaviaPartai politikDSSSuami/istriZorica RadoviÄSunting kotak info âĒ L âĒ B Dr. Vojislav KoÅĄtunica dengarkanâ (bahasa Serbia: ÐÐūŅÐļŅÐŧаÐē ÐÐūŅŅŅÐ―ÐļŅа) (diej...

Genus of flowering plants For other uses, see Malva (disambiguation). Malva Malva sylvestris Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Malvales Family: Malvaceae Subfamily: Malvoideae Tribe: Malveae Genus: MalvaL.[1] Type species M. sylvestris[2] Species See text. Synonyms[3] Anthema Medik. Axolopha Alef. Bismalva Medik. Dinacrusa G.Krebs Lavatera L. Navaea Webb & Berthel. Olbia Medik. Sa...













