Inégalité de Weitzenböck
|
Read other articles:

Further information: Category:Democratic National Conventions and List of presidential nominating conventions in the United States Map of states that have hosted a Democratic National Convention This is a list of Democratic National Conventions. These conventions are the presidential nominating conventions of the Democratic Party of the United States. List of Democratic National Conventions Conventions whose nominees won the subsequent presidential election are tinted in light blue. Four oth...
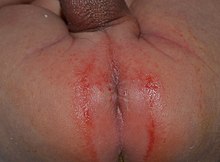
Ruam popok ringan pada bayi laki-laki yang diberi ASI dan popok kain berusia 3 minggu Ruam popok merupakan salah satu jenis gangguan yang terjadi pada kulit manusia. Ruam popok berupa iritasi dan peradangan kulit akibat dari penggunaan popok.[1] Ruam popok ditandai dengan berubahnya warna kulit menjadi kemerahan di beberapa daerah misalnya daerah pantat, lipatan paha, dan juga pada kelamin. Ruam popok memang lebih sering terjadi pada bayi, tapi hal tersebut tidak menutup kemungkinan t...

Cet article est une ébauche concernant le cyclisme. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Milan-San Remo 1961GénéralitésCourse 52e Milan-San RemoCompétition Super Prestige Pernod 1961 (d)Date 19 mars 1961Distance 288 kmPays traversé(s) ItalieLieu de départ MilanLieu d'arrivée San RemoCoureurs au départ 214Coureurs à l'arrivée 126Vitesse moyenne 37,474 km/hRésultatsVainqueur Raymon...

Chiesa abbaziale di San Benedetto MartireVista parziale della facciataStato Italia RegioneMarche LocalitàSan Benedetto del Tronto Indirizzovia Muto, 2 - San Benedetto del Tronto Coordinate42°57′01.77″N 13°52′32.33″E / 42.950492°N 13.875646°E42.950492; 13.875646Coordinate: 42°57′01.77″N 13°52′32.33″E / 42.950492°N 13.875646°E42.950492; 13.875646 ReligioneCattolica TitolareSan Benedetto Diocesi San Benedetto del Tronto-Ripatransone-M...

Peta lokasi burh menurut dokumen abad ke-10 Burghal Hidage. Burh (Pengucapan Inggris lama: [ˈburx]) atau burg adalah sebuah benteng atau kota benteng di Inggris pada zaman bangsa Anglo-Saxon. Pada abad ke-9, Raja Alfred Agung mengembangkan sebuah jaringan burh dan jalan untuk menghadapi serangan-serangan bangsa Viking. Sebagian burh dibangun dari awal, dan sebagian dibangun dengan mengembangkan benteng bukit dari zaman besi maupun benteng-benteng peninggalan Romawi. Banyak juga burh yan...

Pour les articles homonymes, voir 86e régiment. 86e régiment d'infanterie territoriale Permissionnaires du 86e régiment territorial gare de l'Est le 22 novembre 1915. Création août 1914 Dissolution août 1918 Pays France Branche Armée de terre Type Régiment d'infanterie territoriale Rôle Infanterie de soutien Surnom 86 Coz Inscriptionssur l’emblème Somme 1916L'Aisne 1917 Guerres Première Guerre mondiale Batailles Bataille de la SommeBataille du Chemin des Dames mod...

Two-seat military helicopter of the 1940s R-4 / Hoverfly A Sikorsky R-4 in a hover Role HelicopterType of aircraft Manufacturer Sikorsky Aircraft Designer Igor Sikorsky First flight January 14, 1942 Introduction 5 January 1943 Primary users United States Army Air ForcesUnited States Coast Guard Royal Air Force Produced 1942–1944 Number built 131 Developed from Vought-Sikorsky VS-300 Developed into Sikorsky R-6 In this image taken in 1944, one of Langley Research Center's Sikorsky YR-4B...
Coppa di Serbia 2017Piraeus Bank Radivoj Korać Cup 2017Dettagli della competizioneSport Pallacanestro Federazione KSS Periodo16 febbraio 2017 —19 febbraio 2017 Data2017 LuogoNiš ImpiantoSportski centar Čair VerdettiCampione Stella Rossa(6º titolo) MVP Marko Gudurić Cronologia della competizioneed. successiva → ← ed. precedente Modifica dati su Wikidata · Manuale La Coppa Radivoj Korać 2017 è la 15ª Coppa di Serbia di pallacanestro masch...

Wilayah Sheikh Jarrah. Di latar belakang, pusat kota Yerusalem. Sheikh Jarrah (Arab: الشيخ جراح, Ibrani: שייח' ג'ראח) adalah sebuah wilayah Palestina di Yerusalem Timur, yang berjarak 2 kilometer dari Kota Tua, di jalan menuju Gunung Scopus.[1][2] Wilayah tersebut mengambil nama dari makam abad ke-13 Sheikh Jarrah, seorang tabib Saladin, yang berada di wilayah tersebut. Wilayah modern didirikan pada 1865, dan secara bertahap menjadi pusat kediaman elit...

Lembaran sampul Simfoni Eroica yang menunjukkan dedikasi kepada Napoleon yang dihapus I. Allegro con brio (15:12) II. Marcia funebre: Adagio assai (15:29) III. Scherzo: Allegro vivace (5:49) IV. Finale: Allegro molto (11:45) All files courtesy of Musopen Bermasalah memainkan berkas-berkas ini? Lihat bantuan media. Simfoni No. 3 dalam tangga nada Es Mayor (Op. 55), yang dikenal juga sebagai Eroica (bahasa Italia; 'heroik') adalah salah satu karya Ludwig van Beethoven yang merupakan simfoni ket...

الهيئة السعودية للمدن الصناعية ومناطق التقنية مدن—MODON تفاصيل الوكالة الحكومية البلد السعودية الاسم الكامل الهيئة السعودية للمدن الصناعية ومناطق التقنية تأسست 2001 المركز الرياض، السعودية الموظفون 291 (2014) الإدارة الوزراء المسؤولون بندر الخريف، رئيس مجلس الإدار�...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

الأوضاع القانونية لزواج المثليين زواج المثليين يتم الاعتراف به وعقده هولندا1 بلجيكا إسبانبا كندا جنوب أفريقيا النرويج السويد المكسيك البرتغال آيسلندا الأرجنتين الدنمارك البرازيل فرنسا الأوروغواي نيوزيلندا3 المملكة المتحدة4 لوكسمبورغ الولايات المتحدة5 جمهورية أيرلندا ...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مارس 2023) أنتراتسيت علم شعار الاسم الرسمي (بالأوكرانية: Антрацит) الإحداثي�...

Singapore-related events during 1967 This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources. ← 1966 1965 1964 1967 in Singapore → 1968 1969 1970 Decades: 1940s 1950s 1960s 1970s 1980s See also: Other events of 1967 Timeline of Singaporean history The following lists events that happened during 1967 in Singapore. Incumbents President: Yusof Ishak Prime Minister: Lee Kuan Yew Events Ja...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Barn Welsh magazine – news · newspapers · books · scholar · JSTOR (April 2018) (Learn how and when to remove this message) For other uses, see Barn (disambiguation). BarnSeptember 2007 cover of BarnTypeMonthly current affairs magazineFormatMagazineOwner(s)Board of trusteesEditorVaughan Hughes, Menna B...

Artikel ini bukan mengenai Xeon. 54XeXenonGas xenon dalam tabung lucutan Garis spektrum xenonSifat umumNama, lambangxenon, XePengucapan/sénon/[1]/sènon/Penampilangas tak berwarna, akan menjadi biru bila diletakkan pada medan listrik bertegangan tinggiXenon dalam tabel periodik 54Xe Hidrogen Helium Lithium Berilium Boron Karbon Nitrogen Oksigen Fluor Neon Natrium Magnesium Aluminium Silikon Fosfor Sulfur Clor Argon Potasium Kalsium Skandium Titanium Vanadium Chromium Mangan Besi Coba...

Nuclear reactor, Oak Ridge 1965–1969 MSRE plant diagram: (1) Reactor vessel, (2) Heat exchanger, (3) Fuel pump, (4) Freeze flange, (5) Thermal shield, (6) Coolant pump, (7) Radiator, (8) Coolant drain tank, (9) Fans, (10) Fuel drain tanks, (11) Flush tank, (12) Containment vessel, (13) Freeze valve. Also note Control area in upper left and Chimney upper right. The Molten-Salt Reactor Experiment (MSRE) was an experimental molten-salt reactor research reactor at the Oak Ridge National Laborat...

Autoklaf sederhana Sterilisasi atau penyucihamaan adalah pemusnahan atau eliminasi semua mikroorganisme, termasuk spora bakteri, yang sangat resisten.[1] Lihat Pula Mikroorganisme Disinfektan Antiseptik Autoklaf Referensi ^ Levinson W. 2008. Review of Medical Microbiology & Imunology, Tenth Edition. New York: The McGraw-Hill Companies, Inc.

This article is about the spa town in the Wetteraukreis. For the community in Groß-Gerau district, see Nauheim. Town in Hesse, GermanyBad Nauheim TownAerial view Coat of armsLocation of Bad Nauheim within Wetteraukreis district Bad Nauheim Show map of GermanyBad Nauheim Show map of HesseCoordinates: 50°22′N 8°45′E / 50.367°N 8.750°E / 50.367; 8.750CountryGermanyStateHesseAdmin. regionDarmstadt DistrictWetteraukreis Founded900Subdivisions6 districtsGovernment&#...













![{\displaystyle {\begin{aligned}S&{}={\frac {1}{4}}{\sqrt {(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}\\[4pt]&{}={\frac {1}{4}}{\sqrt {2\left(a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2}\right)-\left(a^{4}+b^{4}+c^{4}\right)}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62952aca508d4ae932d779820ebaa9147b241e2f)





![{\displaystyle {\sqrt[{3}]{xyz}}\leqslant {\frac {x+y+z}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ac77d1cab8b0879f86abd2150918fcecb3708b5)








