Herbert John Ryser
|
Read other articles:

Buggerru BugèrruKomuneComune di BuggerruLokasi Buggerru di Provinsi Sardinia SelatanNegara ItaliaWilayah SardiniaProvinsiSardinia Selatan (SU)Pemerintahan • Wali kotaLaura CapelliLuas • Total48,33 km2 (18,66 sq mi)Ketinggian51 m (167 ft)Populasi (2016) • Total1,068[1]Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos09010Kode area telepon0781Situs webhttp://www.comune.buggerru.ci.it Buggerru...

Burger kejuAsalNegara asalAmerika Serikat RincianJenishamburger Bahan utamaRoti bulat, keju dan Patty lbs Burger keju adalah hamburger yang disisipi keju. Pembuatannya adalah keju dipotong tipis, lalu dibiarkan sesaat agar keju meleleh. Di Amerika Serikat, keju yang dipakai kebanyakan adalah keju Amerika, tetapi keju seperti mozzarella, keju biru, keju pepperjack, dan keju Cheddar juga populer. Keju yang ada di dalam burger membuatnya lebih bergizi. Contohnya, dibandingkan burger biasa, sebua...

Traktat Gulistan Nama panjang: Traktat Perdamaian antara Kekaisaran Rusia dan Kekaisaran Persia Perbatasan Iran barat laut sebelum dan sesudah traktatLokasiGulistanEfektif24 Oktober 1813Penanda tangan Nikolai Rtischev Mirza Abolhassan Khan Ilchi Traktat Gulistan (bahasa Rusia: Гюлистанский договор; Persia: عهدنامه گلستان) adalah sebuah traktat perdamaian yang disepakati antara Kekaisaran Rusia dan Persia (kini Iran) pada 24 November 1813 di desa Gulista...

غروس-غيراو علم شعار الإحداثيات 49°55′17″N 8°28′55″E / 49.921388888889°N 8.4818055555556°E / 49.921388888889; 8.4818055555556 [1] تقسيم إداري البلد ألمانيا[2][3] خصائص جغرافية المساحة 54.47 كيلومتر مربع (31 ديسمبر 2017)[4] ارتفاع 88 متر عدد السكان عدد ال...

Academic discipline For the journal, see Middle Eastern Studies (journal). Ceiling of the Mosque-Madrassa of Sultan Barquq, Cairo Middle Eastern studies (sometimes referred to as Near Eastern studies, West Asian Studies or South Western Asian) is a name given to a number of academic programs associated with the study of the history, culture, politics, economies, and geography of the Middle East, an area that is generally interpreted to cover a range of nations including Egypt, Iran, Iraq, Isr...
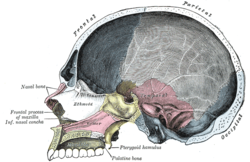
Hook-like process of the sphenoid bone of the skull Pterygoid hamulusSphenoid bone. Anterior and inferior surfaces. (Hamulus labeled at bottom left.)Sagittal section of skull. (Sphenoid is in yellow, and pterygoid hamulus labeled at bottom center.)DetailsPart ofsphenoid bone of skullSystemskeletalIdentifiersLatinhamulus pterygoideusTA98A02.1.05.051TA2637FMA54722Anatomical terms of bone[edit on Wikidata] The pterygoid hamulus is a hook-like process at the lower extremity of the medial pter...

LST1 المعرفات الأسماء المستعارة LST1, B144, D6S49E, LST-1, leukocyte specific transcript 1 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 109170 HomoloGene: 136814 GeneCards: 7940 نمط التعبير عن الحمض النووي الريبوزي المزيد من بيانات التعبير المرجعية أورثولوج الأنواع الإنسان الفأر أنتريه 7940 n/a Ensembl ENSG00000226182، �...

1961 filmHercules and the Conquest of AtlantisDirected byVittorio CottafaviScreenplay by Vittorio Cottafavi Sandro Continenza Duccio Tessari Pierre Benoit Nicolo Ferrari[1] Story byNicolo Ferrari[1]Produced byAchille Piazzi[1]Starring Reg Park Fay Spain Ettore Manni Luciano Marin CinematographyCarlo Carlini[1]Edited byMaurizio Lucidi[1]Music by Gino Marinuzzi Jr. Armando Trovajoli[1] Productioncompanies SpA Cinematografica Comptoir Francais du ...

2006 greatest hits album by Kenny GThe Essential Kenny GGreatest hits album by Kenny GReleasedJanuary 24, 2006GenreJazzLength77:18 (Disc One)77:14 (Disc Two)154:32 (Total)LabelAristaProducerKenny GWalter AfanasieffMichael BoltonPeter BunettaRick ChudacoffDavid FosterPreston GlassJeff MagidDan SheaKenny G chronology The Greatest Holiday Classics(2005) The Essential Kenny G(2006) Best(2006) Professional ratingsReview scoresSourceRatingAllmusic[1] The Essential Kenny G is the fif...

Former American investment bank For other uses of the name Salomon, see Salomon. Salomon Brothers, Inc.1 New York Plaza which was Salomon Brothers' headquarters starting in 1970Company typePublicTraded asNYSE: SBIndustryFinancial servicesFounded1910; 114 years ago (1910)FoundersArthur SalomonHerbert SalomonPercy SalomonDefunct2003; 21 years ago (2003) (name dropped by Citigroup)FateAcquired by Travelers Group in 1997SuccessorSalomon Smith Barney (1997�...

2018 American baseball competition 2018 Major League Baseball All-Star Game 1 2 3 4 5 6 7 8 9 10 R H E American League 0 1 1 0 0 0 0 3 0 3 8 13 0 National League 0 0 1 0 0 0 1 1 2 1 6 7 1 DateJuly 17, 2018VenueNationals ParkCityWashington, D.C.ManagersA. J. Hinch (HOU)Dave Roberts (LAD)MVPAlex Bregman (HOU)Attendance43,843Ceremonial first pitchJames McCloughanTelevisionFox (United States)MLB International (International)TV announcersJoe Buck, John Smoltz, Ken Rosenthal and Tom Verducci (Fox)D...
Commuter town in County Meath, Ireland Town in Leinster, IrelandDunshaughlin Dún Seachlainn/Domhnach SeachnaillTownThe Drumree Road in DunshaughlinDunshaughlinLocation in IrelandCoordinates: 53°30′42″N 6°32′22″W / 53.5118°N 6.5395°W / 53.5118; -6.5395CountryIrelandProvinceLeinsterCountyCounty MeathElevation105 m (344 ft)Population (2022 census)[1]6,644Time zoneUTC+0 (WET) • Summer (DST)UTC-1 (IST (WEST))Irish Grid Referen...

Birk RisaNazionalità Norvegia Altezza188 cm Calcio RuoloDifensore, attaccante Squadra New York City CarrieraGiovanili Sola Sandnes Ulf2014-2017 Colonia Squadre di club1 2014 Sandnes Ulf0 (0)2016-2018 Colonia II20 (3)2017-2018 Colonia2 (0)2018-2020 Odd76 (4)2020-2023 Molde63 (3)2023- New York City0 (0) Nazionale 2013 Norvegia U-152 (2)2014 Norvegia U-167 (1)2015 Norvegia U-1710 (1)2016 Norvegia U-1811 (7)2017 Norvegia U-193 (0)2017-2020 ...

大同鄉Datong Township舊稱:眠腦、濁水、太平山地鄉 鄉徽 大同鄉位置圖 坐标:24°40′38″N 121°36′32″E / 24.6772°N 121.609°E / 24.6772; 121.609國家 中華民國省臺灣省上級區劃宜蘭縣下級區劃10村74鄰政府 • 行政机构大同鄉公所(立法機關:大同鄉民代表會) • 鄉長何勝立(大同鄉鄉長列表)面积 • 总计657.5442 平方公里(253.8792 ...

Scottish League One 2020-2021 Competizione Scottish League One Sport Calcio Edizione 46ª Organizzatore SPFL Date dal 17 ottobre 2020al 6 maggio 2021 Partecipanti 10 Risultati Vincitore Partick Thistle(1º titolo) Retrocessioni Forfar Athletic Statistiche Incontri disputati 110 Gol segnati 278 (2,53 per incontro) Cronologia della competizione 2019-2020 2021-2022 Manuale La Scottish League One 2020-2021 è stata la 46ª edizione di quella che era la Scottish Second Di...

17th c. Glasgow Town Clerk Mr. John SpreulBornSurname is sometimes spelled Spreull or Sprewll[1]1616GlasgowDied1690TitleMr. (being a graduate)SpouseCatherine Merchel (17 November 1640)[2]Children12+ John Spreul (born 1616[2]) was a town clerk in Glasgow who was educated at the University of Glasgow, where he completed his Master of Arts degree in 1635. His father was the Provost of Renfrew and an MP for Renfrew.[3] After university, he thought about becoming a ...

Independence Hall, Philadelphia Deklarasi Kemerdekaan oleh John Trumbull Kongres Kontinental Kedua merupakan sebuah nama yang diberikan kepada majelis delegasi dari 13 koloni Amerika Serikat yang berlangsung pada 10 Mei 1775 hingga 1 Maret 1781. Kongres ini menyetujui Deklarasi Kemerdekaan Amerika Serikat pada 4 Juli 1776, mangeak Pasal-Pasal Konfederasi. Selama Revolusi Amerika Serikat, Kongres ini bertindak sebagai pemerintah dan membuat keputusan mengenai kebijakan luar negeri, perang, dan...

Stefan KuntzKuntz nel 2018Nazionalità Germania Ovest Germania (dal 1990) Altezza180 cm Peso84 kg Calcio RuoloAllenatore (ex attaccante) Termine carriera1999 - giocatore CarrieraGiovanili 1969-1980 Borussia Neunkirchen Squadre di club1 1980-1983 Borussia Neunkirchen? (?)1983-1986 Bochum100 (41)1986-1989 Bayer Uerdingen94 (32)1989-1995 Kaiserslautern170 (75)1995-1996 Beşiktaş30 (9)1996-1998 Arminia Bielefeld65 (25)1998-1999 Bochum20 (6) Nazionale ...

「IGBT」はこの項目へ転送されています。「LGBT」とは異なります。 この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 絶縁ゲートバイポーラトランジスタ – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib...

Mathematical function with no sudden changes Part of a series of articles aboutCalculus ∫ a b f ′ ( t ) d t = f ( b ) − f ( a ) {\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)} Fundamental theorem Limits Continuity Rolle's theorem Mean value theorem Inverse function theorem Differential Definitions Derivative (generalizations) Differential infinitesimal of a function total Concepts Differentiation notation Second derivative Implicit differentiation Logarithmic differ...

