Estimation stochastique en mécanique des fluides
|
Read other articles:

Rapid transit system in the city of Chennai, India Chennai MonorailOverviewNative nameசென்னை மோனோரெயில்LocaleChennai, Tamil NaduTransit typestraddle-beam MonorailNumber of lines3 (Phase I)HeadquartersChennaiOperationOperation will start2018 (Estd. But later plan was cancelled and Chennai metro was constructed)Train length4 coachesHeadway3 minutesTechnicalSystem length57 km (Phase I)Electrification750 V DCAverage speed65 km/h (40 mph)Top speed80&#...

Doli Saja Ke RakhnaSutradaraPriyadarshanProduserRajkumar Santoshi(Presenter)Xavier MarquisRaman MarooDitulis olehNeeraj Vora(Screenplay & Dialogue)CeritaFazilPemeranAkshaye KhannaJyothikaPenata musikA. R. RahmanSinematograferK. V. AnandPenyuntingN. GopalakrishnanPerusahaanproduksiShemaroo EntertainmentDistributorShemaroo EntertainmentTanggal rilis27 November 1998NegaraIndiaBahasaHindi Doli Saja Ke Rakhna adalah film Bollywood tahun 1998 yang bergenre romantis yang disutradarai oleh ...
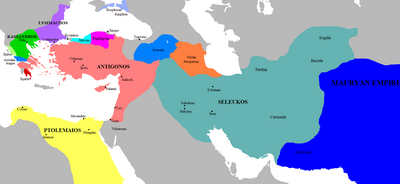
Battle in 301 BC that ended the Fourth War of the Diadochi Battle of IpsusPart of the Wars of the DiadochiThe Battle of Ipsus in 301 BC. 19th century engraving.Date301 BCLocationIpsus, Phrygia(modern-day Çayırbağ, Afyonkarahisar, Turkey)38°57′N 30°59′E / 38.95°N 30.99°E / 38.95; 30.99Result Coalition victoryBelligerents Antigonids Lysimachids Antipatrids Seleucids Commanders and leaders Antigonus I Monophthalmus † Demetrius I Pyrrhus Lysimachus Se...

Abjad SafaJenis aksara Abjad BahasaArab KunoPeriodeAbad ke-1 SM hingga abad ke-4 MAksara terkaitSilsilahHieroglif MesirAbjad Proto-SinaiAbjad Semit SelatanAbjad SafaAksara kerabatAbjad Arabia Utara Kuno, Abjad Arabia Selatan Kuno, Aksara Ge'ez Artikel ini mengandung transkripsi fonetik dalam Alfabet Fonetik Internasional (IPA). Untuk bantuan dalam membaca simbol IPA, lihat Bantuan:IPA. Untuk penjelasan perbedaan [ ], / / dan ⟨ ⟩, Lihat IPA § Tan...

Polish physicist (1913–1989) Jerzy PniewskiPniewski in 1967Born(1913-06-01)June 1, 1913Płock, Congress PolandDiedJune 16, 1989(1989-06-16) (aged 76)Warsaw, PolandNationalityPolishAlma materUniversity of WarsawKnown forDiscovery of hypernucleusAwardsMarian Smoluchowski Medal (1969)Order of Polonia Restituta (1974)Scientific careerInstitutionsPolish Academy of Sciences Jerzy Pniewski (Polish: [ˈjɛʐɨ ˈpɲɛfskʲi]; June 1, 1913 – June 16, 1989) was a Polish physicis...

Cet article est une ébauche concernant la littérature américaine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (mars 2023). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléte...

Communication campaign Be Brave Like UkraineProduced byBanda AgencyCountry UkraineWebsitehttps://brave.ua Be Brave Like Ukraine (Ukrainian: Будь сміливим, як Україна) or Bravery (Ukrainian: Сміливість) is a communication campaign created during the full-scale Russian invasion of Ukraine in 2022.[1] The campaign which is claimed to be part of Ukrainian propaganda[2][3] is designed to highlight the main feature of Ukrainians. It w...

Эта статья — о части растения. О форме тела животных см. Стробила. У Хвоща лесного, как и у большинства других хвощевидных, стробилы возникают на концах стеблей Стро́билы (лат. strobilus от др.-греч. στρόβῑλος — кубарь, сосновая или еловая шишка) — органы раз�...

Лягушки-поросята Мраморная лягушка-поросёнок Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКласс:Земн...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Political magazine in Sweden (1999–2002) SaltEditor-in-chiefPer-Olof BolanderJonas De GeerÅsa LjungquistCategoriesPolitical magazineFrequencyThree or four times per yearFounded1999First issueOctober 1999Final issue2002CountrySwedenBased inStockholmGothenburgLanguageSwedishISSN1404-6938OCLC185386199 This article is part of a series onConservatism in Sweden Ideologies Christian democracy Liberal Moderate Nationalist Principles Cameralism Duty Elitism Meritocracy Law and order Moderation Lago...
Philip HaasPassport photograph from 1924 with signatureBorn(1874-06-07)June 7, 1874Michelstadt, Odenwaldkreis, Hesse, GermanyDied(1927-09-30)September 30, 1927Dayton, Montgomery, Ohio, U.S.NationalityGermanEducationDayton Public SchoolsOccupation(s)Inventor, entrepreneurSpouseCatherine Steiger (1877-1960)ChildrenAlbertina Anna Haas (1900-1981)Marie K Haas (1903-1969)Helen Anna Haas (1906-1984)Alma Helen Haas (1908-1976)Esther Haas (1917-)Martha Nancy Haas (1918-1919)Parent(s)Michael Johann Ha...

Early English colonist in North America For the pediatrician, see John Howland (doctor). John Howland (c. 1593 – February 23, 1673) was an English indentured servant who accompanied the English Separatists and other passengers when they left England on the Mayflower to settle in Plymouth Colony. In later years, he was an executive assistant and personal secretary to Governor John Carver.[1] In 1620 he signed the Mayflower Compact and helped found the colony.[2...

Questa voce o sezione sull'argomento artiodattili non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Come leggere il tassoboxOriceClassificazione scientificaDominioEukaryota RegnoAnimalia PhylumChordata ClasseMammalia OrdineArtiodactyla FamigliaBovidae SottofamigliaHippotraginae GenereOryx Specie Oryx beisa Oryx dammah Oryx leucoryx Oryx gazella Gli orici s...

Several types of leg coverings A woman wearing black leggings Leggings are several types of leg attire that have varied through the years. Modern usage from the 1960s onwards has come to refer to elastic close-fitting high-rise garments worn over the legs typically by women, such as leg warmers or tights. Usage from the 18th century refers to men's wear usually made of cloth or leather that is wrapped around the leg down to the ankle.[1] In the 19th century, leggings usually referred ...

Fifth Avenue Museum Mile Lalu lintas pusat kota yang melewati Metropolitan Museum of Art di 81st Street didominasi oleh bus dan taksi.Pemilik City of New YorkPengelola NYCDOTPanjang 6.197 mi[1][2] (9,973 km)Lokasi Manhattan, New York CityUjung selatan Washington Square North di Greenwich VillagePersimpanganbesar Madison Square di FlatironGrand Army Plaza di MidtownDuke Ellington Circle di East HarlemMarcus Garvey Park di HarlemMadison Avenue Bridge di Harlem Harlem River ...

黑紗白眼蝶 黑紗白眼蝶 (第四行,左一) 保护状况 未予评估(IUCN 3.1) 科学分类 界: 动物界 Animalia 门: 节肢动物门 Arthropoda 纲: 昆虫纲 Insecta 目: 鱗翅目 Lepidoptera 总科: 鳳蝶總科 Papilionoidea 科: 蛺蝶科 Nymphalidae 亚科: 眼蝶亞科 Satyrinae 属: 白眼蝶属 Melanargia 种: 黑紗白眼蝶 M. lugens 二名法 Melanargia lugensHonrath, 1888 異名 Melanargia helimede var. lugensHonrath, 1888 黑紗白眼蝶(�...

Voce principale: Campionato mondiale di Formula 1 1999. Gran Premio di Monaco 1999 634º GP del Mondiale di Formula 1Gara 4 di 16 del Campionato 1999 Data 16 maggio 1999 Luogo Circuito di Monte Carlo Percorso 3,367 km / 2,092 US mi circuito cittadino Distanza 78 giri, 262,626 km/ 163,196 US mi Clima soleggiato Risultati Pole position Giro più veloce Mika Häkkinen Mika Häkkinen McLaren - Mercedes in 1'20547 McLaren - Mercedes in 1'22259 (nel giro 67) Podio 1. Michael SchumacherFerrar...
List of options or commands within a computer program This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Menu computing – news · newspapers · books · scholar · JSTOR (September 2021) (Learn how and when to remove this message) A drop-down menu of file operations in a Microsoft Windows program In user inter...

اضغط هنا للاطلاع على كيفية قراءة التصنيف بندقوطياتالعصر: Late Oligocene–Recent قك ك أ س د ف بر ث ج ط ب ن جرذ خنزيري قصير الأنف المرتبة التصنيفية رتبة[1][2] التصنيف العلمي المملكة: حيوان الشعبة: حبليات الطائفة: ثدييات الطائفة السفلى: وخفيات الرتبة: بندقوطيات الشكلأميغينو, 1889...












![{\displaystyle A=[A({\vec {x_{i}}}),B({\vec {x_{i}}},{\vec {x_{j}}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20fd44001c55383e9b0f3533b40936f29b64f350)

![{\displaystyle A=[E^{T}E]^{-1}E^{T}U}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20af875a7456d40862e839558b7052cf54e3fe8b)





