Ensemble partiellement ordonné
|
Read other articles:

Pindad MV2 Purwarupa MV2 Jenis SUV, Kendaraan utilitas militer ringan Negara asal Indonesia Sejarah produksi Perancang Pindad Produsen Pindad Diproduksi 2021 – sekarang Spesifikasi Berat 2.630 kilogram (5.800 pon) (kosong)3.200 kilogram (7.100 pon) (penuh) Panjang 5.220 mm (205,5 in) Lebar 2.010 mm (79,1 in) Tinggi 1.860 mm (73,2 in) Jenis Mesin 136 tenaga kuda (101 kW) Transmisi Manual (6 maju dan 1 mundur) Suspensi Independent double...

Ganggang hijau Alga hijau adalah kelompok alga berdasarkan zat warna atau pigmentasinya. Alga hijau memiliki anggota sekitar 7.000 spesies.[1] Alga hijau juga merupakan alga uniseluler maupun multiseluler yang memiliki klorofil yang dominan yang membuat alga berwarna hijau.[2] Dalam taksonomi, semula semua alga yang tampak berwarna hijau dimasukkan sebagai salah satu kelas dalam filum/divisio Thallophyta, yaitu Chlorophyceae. Pengelompokan ini sekarang dianggap tidak valid kar...

Disambiguazione – Se stai cercando altri significati, vedi 1919 (disambigua). XIX secolo · XX secolo · XXI secolo Anni 1890 · Anni 1900 · Anni 1910 · Anni 1920 · Anni 1930 1915 · 1916 · 1917 · 1918 · 1919 · 1920 · 1921 · 1922 · 1923 Il 1919 (MCMXIX in numeri romani) è un anno del XX secolo. 1919 negli altri calendari Calendario gregoriano 1919 Ab Urbe condita 2672 (MMDCLXXII) Calendario armeno...

Di Bulan Suci Ini...Genre Drama Komedi Ditulis oleh Titien Wattimena Tamara Citra Deliesza Skenario Beta Ingrid Ayu Ummu Amalia Misbah CeritaDinna JasantiSutradaraDinna JasantiPemeran Titi Kamal Rebecca Klopper Dennis Adhiswara Verdi Solaiman Jenny Zhang Penggubah lagu temaYudhistira AriantoLagu penutupRamadhan Datang oleh TompiNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim1Jmlh. episode6ProduksiProduser eksekutif Anthony Buncio Sutanto Hartono Monika Rudijono ProduserWicky V. Ol...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of films of the Church of Jesus Christ of Latter-day Saints – news · newspapers · books · scholar · JSTOR (July 2018) (Learn how and when to remove this template message) Part of a series on theBook of Mormon Origin Cumorah Golden plates Joseph Smith Emma...

Левий Матфейивр. מַתִּתְיָהוּ Евангелист Матфей. Византия. XIV век; местонахождение: Греция, Афон, монастырь Хиландар. Родился I векЗемля Израильская, Израиль Умер 74Эфиопия В лике апостолов Главная святыня мощи в кафедральном соборе Святого Матфея в Салерно, Итали...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Земская почтаУезды Алатырский Александрийский Ананьевский Ардатовский Арзамасский Аткарский Ахтырский Балашовский Бахмутский Бежецкий Белебеевский Белозерский Бердянский Бобровский Богородский Богучарский Борисоглебский Боровичский Бронницкий Бугульминский Бу�...

Федеральное агентство по делам Содружества Независимых Государств, соотечественников, проживающих за рубежом, и по международному гуманитарному сотрудничествусокращённо: Россотрудничество Общая информация Страна Россия Юрисдикция Россия Дата создания 6 сентября...

Komando Wilayah Pertahanan I meliputi seluruh wilayah Sumatra. Markas Komando terdapat di Kota Medan, Sumatera Utara. Kowilhan I diresmikan pada tanggal 3 Desember 1969.[1] Sejak tanggal 25 Mei 1973 wilayah Komando Wilayah Pertahanan I meliputi seluruh wilayah Sumatra dan Kalimantan Barat. Pada tanggal 15 Juli 1985 Kowilhan I Sumatra dan Kalimantan Barat dilikuidasi.[2] Satuan Komando Daerah Kodam Komando Daerah Militer (Kodam) I/Iskandar Muda Komando Daerah Militer (Kodam) II...

Uto-Aztecan language spoken in Mexico Pima BajoO'ob No'okNative toMexicoRegionChihuahua, SonoraEthnicityPima BajoNative speakers740 (2015)[1]Language familyUto-Aztecan Southern Uto-AztecanTepimanPima BajoLanguage codesISO 639-3piaGlottologpima1248ELPO'obChihuahua Lower Pima is classified as Definitely Endangered by the UNESCO Atlas of the World's Languages in Danger Pima Bajo (Mountain Pima, Lowland Pima, Nevome) is a Mexican indigenous language of the Piman branch of the Ut...

Questa voce o sezione sugli argomenti giuristi italiani e politici italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti dei progetti di riferimento 1, 2. Pietro De Francisci Ministro di Grazia e giustiziaDurata mandato20 luglio 1932 –24 gennaio 1935 PredecessoreAlfredo Rocco SuccessoreArrigo Solmi Deputato del Reg...

Mark TettoLahir1 Maret 1980 (umur 44)New JerseyPendidikanUniversitas Princeton (BA)Wharton School (MBA)PekerjaanRekan pada TCK investmentsSitus webMark Tetto di Instagram Mark Tetto (lahir 1 Maret 1980) adalah orang Amerika Serikat yang tinggal dan tampil di Korea Selatan sebagai tokoh televisi dan pebisnis.[1] Ia menjadi anggota dalam acara varietas Non Summit dan Where Is My Friend's Home.[2][3][4] Referensi ^ 오예린 (December 15, 2014). ‘비정상...

Russian news agency This article is about the Russian news agency Interfax. For the Ukrainian news agency named Interfax, see Interfax-Ukraine. InterfaxNative nameИнтерфаксCompany typePrivate limited companyIndustryNews mediaFoundedSeptember 1989 (1989-09)Headquarters1st Tverskaya-Yamskaya str. 2, Moscow, RussiaArea servedWorldwideKey peopleMikhail Komissar [ru](chairman and CEO)Vladimir Gerasimov(executive director; Interfax Group. general director)ProductsWir...
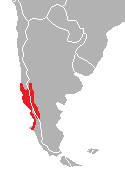
For the district in Kuala Lumpur, Malaysia, see Pudu, Kuala Lumpur.For the 15th day of the Ghost Festival, see the Ghost Festival, see Pudu (disambiguation).Genus of mammals belonging to the deer, muntjac, roe deer, reindeer, and moose family of ruminants PuduTemporal range: Pleistocene – recent Southern pudu (P. puda) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Artiodactyla Family: Cervidae Subfamily: Capreolinae Tribe: Odocoileini ...

1949 film by Alfred Hitchcock Under CapricornAustralian theatrical posterDirected byAlfred HitchcockWritten byHume Cronyn (adaptation)James Bridie (screenplay)Based onUnder Capricornby Helen SimpsonUnder Capricornby John Colton and Margaret LindenProduced byAlfred HitchcockSidney BernsteinStarringMichael WildingIngrid BergmanJoseph CottenMargaret LeightonNarrated byEdmond O'BrienCinematographyJack CardiffEdited byBert BatesMusic byRichard AddinsellLouis LevyProductioncompanyTransatlantic Pict...

German biologist, philosopher, physician, and artist (1834–1919) Haeckel redirects here. For other uses, see Haeckel (disambiguation). Ernst HaeckelBornErnst Heinrich Philipp August Haeckel(1834-02-16)16 February 1834Potsdam, Kingdom of PrussiaDied9 August 1919(1919-08-09) (aged 85)Jena, GermanyAlma mater University of Berlin University of Würzburg University of Jena Known forRecapitulation theorySpouse(s)Anna Sethe, Agnes HuschkeAwards Linnean Medal (1894) Darwin–Wallace ...

Carlo Giuseppe Benedetto Mercy d'Argenteauarcivescovo della Chiesa cattolicaMons. Mercy d'Argenteau in una litografia di Franz Seraph Hanfstaengl Incarichi ricoperti Arcivescovo titolare di Tiro (1826-1879) Vicario apostolico di Anhalt (1834-1837) Nunzio apostolico in Baviera (1826-1837) Decano della Cattedrale di Liegi (1837-1879) Nato17 marzo 1787 a Liegi Ordinato presbitero10 agosto 1825 Nominato arcivescovo2 ottobre 1826 da papa Leone XII Consacrato arcivescovo8 ottobre 1826 d...

Monoclonal antibody treatment for COVID-19 Tixagevimab/cilgavimabTixagevimab (teal, right) and cilgavimab (purple, left) binding the spike protein RBD. From PDB: 7L7E.Combination ofTixagevimabMonoclonal antibodyCilgavimabMonoclonal antibodyClinical dataTrade namesEvusheldOther namesAZD7442AHFS/Drugs.comMonographMedlinePlusa621058License data US DailyMed: Tixagevimab Pregnancycategory AU: B2[1][2][3] Routes ofadministrationIntramuscularATC codeJ06B...

Ne doit pas être confondu avec Perrouse. Pour les articles homonymes, voir Pérouse (homonymie). Cet article est une ébauche concernant une commune du Territoire de Belfort. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Le bandeau {{ébauche}} peut être enlevé et l’article évalué comme étant au stade « Bon début » quand il comporte assez de renseignements encyclopédiques concernant la commune. Si vous avez un doute, l’atelier de lecture ...








![{\displaystyle R[X_{1},...,X_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b8a859b3140b6d65a308278044cf845d09f31a7)





![{\displaystyle [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)