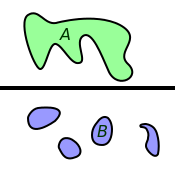
Connexité (mathématiques)
|
Read other articles:

Pamela AndersonPamela Anderson (2017)LahirPamela Denise AndersonNama lainPamela Anderson LeeSuami/istriRick Salomon (October 6, 2007 - February 22, 2008; annulled) Kid Rock (August 3, 2006 - November 27, 2006; bercerai) Tommy Lee (February 19 1995 - February 28 1998; bercerai) 2 anakSitus webhttp://www.pamelachannel.com Pamela Denise Anderson (lahir 1 Juli 1967) merupakan seorang aktris, model, dan penulis berkebangsaan Kanada. Dia dikenal dengan nama Pamela Anderson Lee setelah menikah...

Aïssa Mandi Mandi bersama timnas Aljazair pada 2014Informasi pribadiNama lengkap Aïssa MandiTanggal lahir 22 Oktober 1991 (umur 32)Tempat lahir Châlons-en-Champagne, PrancisTinggi 1,86 m (6 ft 1 in)Posisi bermain BekInformasi klubKlub saat ini VillarrealNomor 23Karier junior2000–2009 ReimsKarier senior*Tahun Tim Tampil (Gol)2009–2016 Reims 160 (14)2016–2021 Real Betis 152 (7)2021– Villarreal 45 (1)Tim nasional‡2014– Aljazair 82 (4) Prestasi Sepak bola Mewak...

Katedral Marsico NuovoKatedral Santa Maria Diangkat ke Surga dan Santo GeorgiusItalia: Concattedrale di S. Maria Assunta o S. Giorgiocode: it is deprecated Katedral Marsico NuovoLokasiMarsico NuovoNegaraItaliaDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupanKeuskupan Agung Potenza-Muro Lucano-Marsico Nuovo Katedral Marsico Nuovo (Italia: Concattedrale di Marsico Nuovo; Concattedrale di Santa Maria Assunta e San Giorgiocode: it is deprecated ) ada...

United States historic placeThe NarragansettU.S. National Register of Historic Places Show map of Chicago metropolitan areaShow map of IllinoisShow map of the United StatesLocation1640 E. 50th St., Chicago, IllinoisCoordinates41°48′16″N 87°35′05″W / 41.80444°N 87.58472°W / 41.80444; -87.58472 (Narragansett, The)Arealess than one acreBuilt1928 (1928)ArchitectLeichenko and EsserArchitectural styleArt DecoNRHP reference No.05000107&...

American writer, editor, and publisher Clifford MethMeth, photographed in 2012BornRockaway, New Jersey, U.S.NationalityAmericanArea(s)Writer, Editor, PublisherNotable worksAardwolf Publishing Clifford Meth is an American writer, editor, and publisher best known for his dark fiction, as well as his publishing imprint Aardwolf Publishing. He has said that his work is often self-consciously Jewish.[1] Early life Meth grew up in Rockaway, New Jersey, and attended Morris Hills High School....

Partai Solidaritas Afghanistan حزب همبستگی افغانستانKetua umumDawood Razmak[1]Dibentuk17 April 2004Kantor pusatKabulKeanggotaan30,000 (approx.)[2]IdeologiSekularismeDemokrasi sosialSosialisme demokratisProgresivismeFeminisme sosialisDemokratisasiReformismeAnti-imperialismeNasionalisme sayap kiriPosisi politikSayap kiriAfiliasi internasionalProgressive International[3]Situs webwww.hambastagi.org/new/en/ Partai Solidaritas Afghanistan (bahasa Pers...

Lambang bahaya radiasi pengion Radiasi pengion adalah radiasi yang membawa energi yang cukup untuk melepaskan elektron dari atom atau molekul, sehingga mengionisasi atom atau molekul tersebut. Radiasi pengion terdiri dari partikel subatomik, ion atau atom yang energetik yang bergerak dengan kecepatan tinggi (biasanya lebih besar dari 1% dari laju cahaya), dan gelombang elektromagnetik pada ujung energi tinggi dari spektrum elektromagnetik. Sinar gama, sinar X, dan sinar ultraviolet yang beren...

Atotoztli IIHuitzilxochtzinCihuātlahtoāni Persekutuan Tiga Kaum AztekPenguasa MexicaPutri AtotoztliBerkuasa1466 - 1472PendahuluAhuitzotlPenerusAxayacatlAyahMotecuzoma IIbuChichimecacihuatzin IPasanganTezozomocAnakAxayacatlTizocAhuitzotl Atotoztli (Nahuatl Klasik: Atotoztli [atoˈtostɬi]) atau Huitzilxochtzin (Nahuatl Klasik: Huitzilxōchtzin [witsiɬˈʃoːtʃtsin]) adalah anak perempuan kaisar Aztek yang bernama Motecuzoma I. Ibunya adalah Chichimecacihuatzin I, yang merupakan ana...

The Darius vase in the Archaeological Museum of Naples (340-320 BCE). The Darius Vase is a famous vase painted by an anonymous Magna Graecia Apulian vase painter, commonly called the Darius Painter, the most eminent representative at the end of the Ornate Style in South Italian red-figure vase painting. The vase was produced between 340 and 320 BCE, probably in a large factory-like workshop in the Greek city of Taranto (ancient Taras), Magna Graecia, well before the fall of Taranto to the Rom...

Cet article est une ébauche concernant le Concours Eurovision de la chanson et la Serbie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) ; pour plus d’indications, visitez le projet Eurovision. Serbieau Concours Eurovision 2009 Données clés Pays Serbie Chanson Cipela Interprète Marko Kon & Milan Nikolić Compositeur Milan 'Milaan' Nikolić, Marko Kon et Aleksandar Milanović Kobac Parolier Marko Kon Langue Serbe Sélection nationale Type de s�...

Stasiun Meiden Nagasawa名電長沢駅Stasiun Meiden Nagasawa, April 2018LokasiOtowa Nagasawacho, Toyokawa-shi, Aichi-ken 441-0203JepangKoordinat34°52′18″N 137°17′18″E / 34.8718°N 137.2882°E / 34.8718; 137.2882Koordinat: 34°52′18″N 137°17′18″E / 34.8718°N 137.2882°E / 34.8718; 137.2882Operator MeitetsuJalur■ Jalur Meitetsu NagoyaLetak15.0 kilometer dari ToyohashiJumlah peron2 peron sampingInformasi lainStatusTanpa stafK...

العلاقات الطاجيكستانية الليبيرية طاجيكستان ليبيريا طاجيكستان ليبيريا تعديل مصدري - تعديل العلاقات الطاجيكستانية الليبيرية هي العلاقات الثنائية التي تجمع بين طاجيكستان وليبيريا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية �...

Village in Sandoval County, New Mexico, United States For the community in Doña Ana County, see San Ysidro, Doña Ana County, New Mexico. Village in New Mexico, United StatesSan Ysidro, New MexicoVillageOld church in San YsidroLocation of San Ysidro, New MexicoSan Ysidro, New MexicoLocation in the United StatesCoordinates: 35°33′38″N 106°46′25″W / 35.56056°N 106.77361°W / 35.56056; -106.77361CountryUnited StatesStateNew MexicoCountySandovalArea[1]&...

NABC Player of the YearAwarded forthe most outstanding men's basketball players in all levels of competitionCountryUnited StatesPresented byNABC State Farm InsuranceHistoryFirst award1975Most recentNCAA DI: Zach Edey, PurdueNCAA DII: KJ Jones II, EmmanuelNCAA DIII: Logan Pearson, Wisconsin–PlattevilleNAIA: Elijah Moore, GraceTwo-year schools: Curt Lewis, John A. LoganWebsiteOfficial website The NABC Player of the Year is an award given annually by the National Association of Basketball Coac...

1932 painting by Pablo Picasso Nude, Green Leaves and BustFrench: Nu au Plateau de SculpteurArtistPablo PicassoYear1932 (1932)MediumOil on canvasDimensions162 cm × 130 cm (64 in × 51 in)LocationPrivate collection (Currently on long-term loan to Tate Modern) Nude, Green Leaves and Bust (French: Nu au Plateau de Sculpteur) is a 1932 oil on canvas painting by Pablo Picasso, featuring his mistress Marie-Thérèse Walter. The painting was in the per...

African-American memoirist (born c. 1858) Annie BurtonBornAnnie Louise Burtonc. 1858Clayton, Alabama, U.S.Died?U.S.Notable workMemories of Childhood's Slavery Days (1909) Annie L. Burton (c. 1858 – ?) was an African American memoirist, whose life story is captured in her 1909 autobiography and slave narrative Memories of Childhood's Slavery Days.[1] Her date of death is uncertain. Biography Annie Louise Burton was born into slavery on a plantation near Clayton, Alabama, and was...

Empat kapal induk, Principe de Asturias, USS Wasp, USS Forrestal and HMS Invincible (depan ke belakang). Perbandingan beberapa kapal induk. Kapal induk (bahasa Inggris: aircraft carrier) adalah sebutan untuk kapal perang yang memuat pesawat tempur dalam jumlah banyak. Tugas utamanya adalah memindahkan kekuatan udara ke dalam armada angkatan laut sebagai pendukung operasi-operasi angkatan laut sekaligus sebagai pusat komando operasi dan kekuatan detterence atau memberikan efek gentar pada lawa...

Dinasti Trần陳朝Trần Triều1225–1400Perluasan dinasti Trần dari tahun 1301 hingga 1337.Wilayah Dinasti Trần pada tahun 1306, setelah pernikahan putri Vietnam Huyền Trân dan raja Champa Chế Mân. Provinsi Thuận Hóa diserahkan kepada Đại Việt.StatusInternal imperial system within Chinese tributary[1][2](Song 1225–1258)(Yuan 1258–1368)(Ming 1368–1400)Ibu kotaThăng Long(1225–1397)Thanh Hóa(1397–1400)Bahasa yang umum digunakanSastra Tiongk...

Daily broadsheet newspaper in the US The Baltimore SunLight for AllThe March 27, 2024 front pageof The Baltimore SunTypeDaily newspaperFormatBroadsheetOwner(s)David D. Smith and Armstrong WilliamsPublisherTrif Alatzas[1]EditorTrif AlatzasFoundedMay 17, 1837; 187 years ago (1837-05-17)Headquarters200 St. Paul PlaceCityBaltimore, Maryland, U.S.CountryUnited StatesCirculation43,000 daily 125,000 Sunday (as of 2021[update])[2]ISSN1930-8965OCLC number24448...

Vidhan Sabha constituencyHarlakhiConstituency No. 31 for the Bihar Legislative AssemblyConstituency detailsCountryIndiaRegionEast IndiaStateBiharDistrictMadhubaniEstablished1951ReservationNoneMember of Legislative Assembly17th Bihar Legislative AssemblyIncumbent Sudhanshu Shekhar PartyJanata Dal (United)Elected year2020 Harlakhi Assembly constituency is an assembly constituency in Madhubani district in the Indian state of Bihar. Overview As per Delimitation of Parliamentary and Assembly cons...